
Dynamic and Distributed Algorithms for Sampling from Gibbs Distributions Yitong Yin Nanjing University &鷂
Dynamic and Distributed Algorithms for Sampling from Gibbs Distributions Yitong Yin Nanjing University

Gibbs Distribution G=V,E) ·q≥2 spin states ·each v∈V,distribution b,:[q]→[0,l] Ae·each e∈E,symmetric A:[q]2→[0,l] ∀configuration o∈[glV: w(o)=A(o,o,)Πb,(o,) e={u,v}∈E v∈V Gibbs distribution:u(o)= where Z= Z ∑w(o) aElg]v
Gibbs Distribution w(σ) = ∏ e={u,v}∈E Ae (σu, σv)∏ v∈V bv (σv) e v bv Ae G = (V, E) • spin states • each , distribution • each , symmetric q ≥ 2 v ∈ V bv : [q] → [0,1] e ∈ E Ae : [q] 2 → [0,1] ∀configuration σ ∈ [q] V : Gibbs distribution: μ(σ) = where w(σ) Z Z = ∑ σ∈[q] V w(σ)
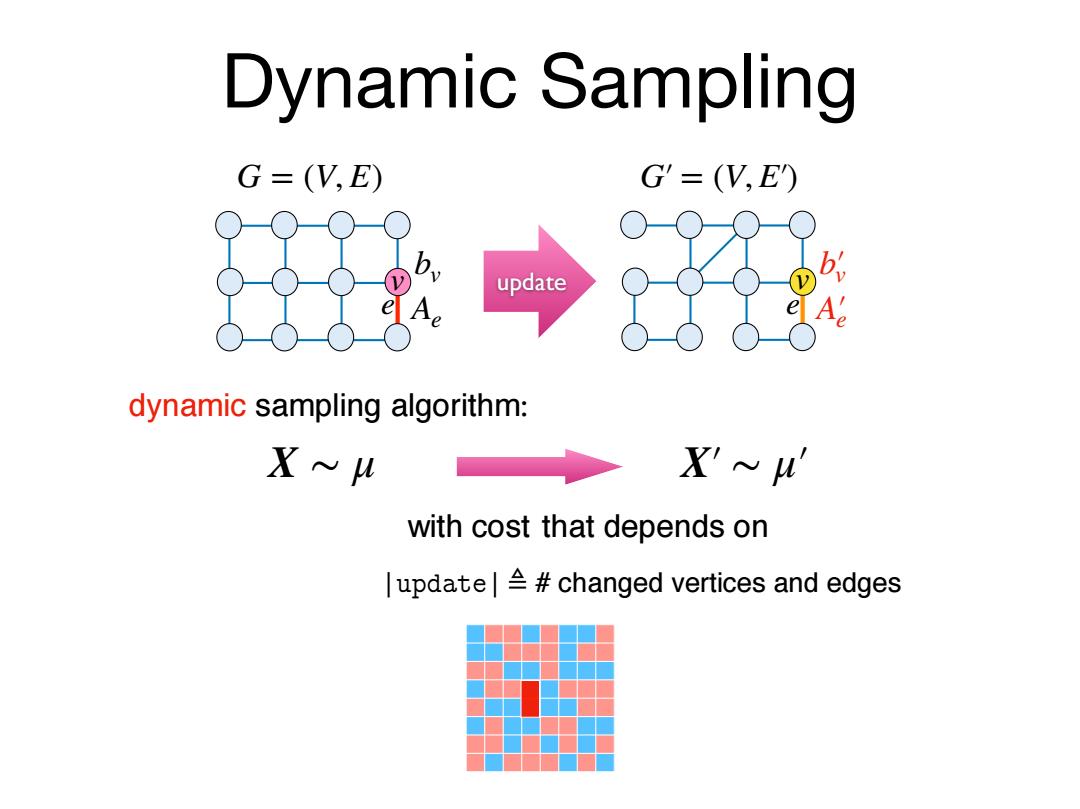
Dynamic Sampling G=(V,E) G'=(V,E) update A dynamic sampling algorithm: Xベu X'u with cost that depends on |update#changed vertices and edges
that depends on Dynamic Sampling e v bv Ae G = (V, E) e v b′ v A′ e G′ = (V, E′) update dynamic sampling algorithm: X ∼ μ X′ ∼ μ′ with cost |������| ≜ # changed vertices and edges
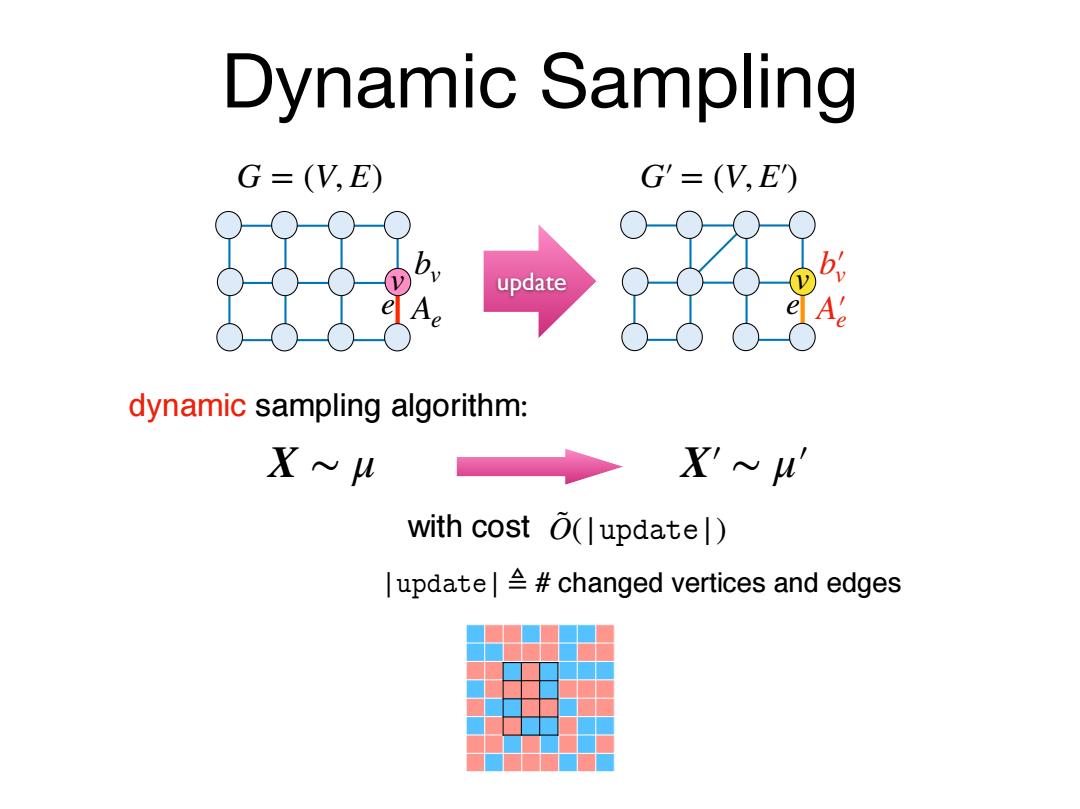
Dynamic Sampling G=(V,E) G'=(V,E) update A dynamic sampling algorithm: X~u X'ベu with cost O(|updatel) |update#changed vertices and edges
Dynamic Sampling e v bv Ae G = (V, E) e v b′ v A′ e G′ = (V, E′) update dynamic sampling algorithm: X ∼ μ X′ ∼ μ′ with cost |������| ≜ # changed vertices and edges O˜(|������|)
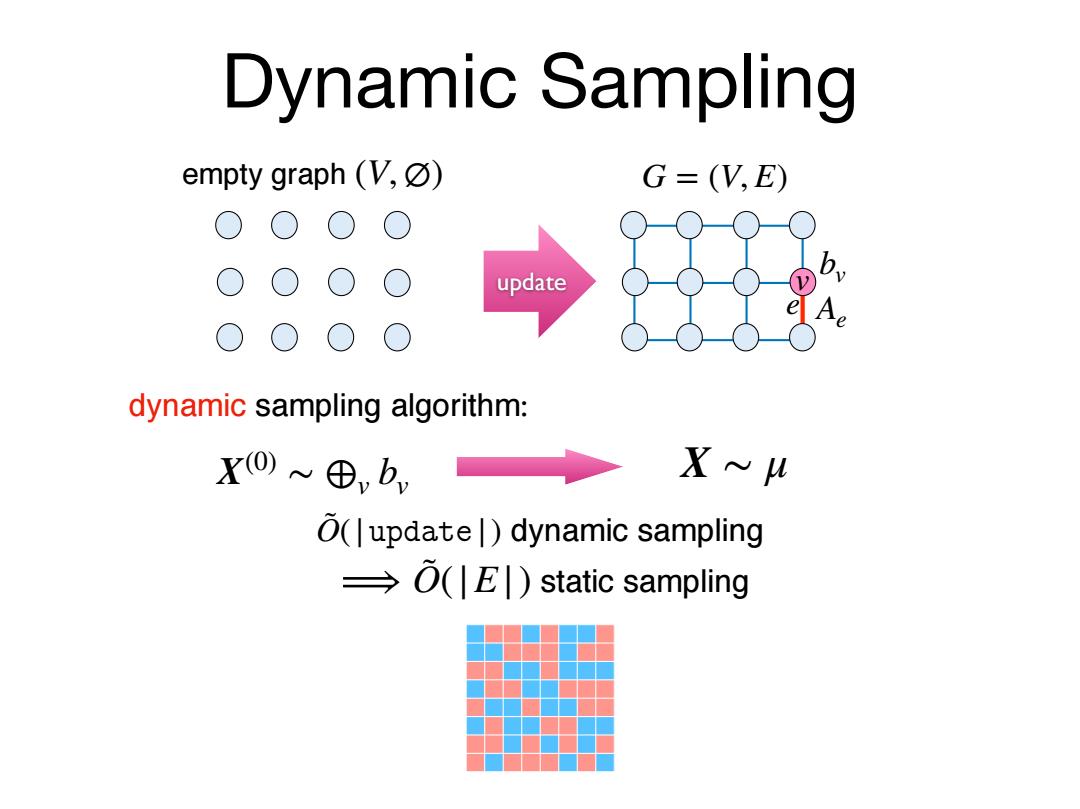
Dynamic Sampling empty graph(V,☑) G=V,E) update dynamic sampling algorithm: X0)~⊕,b, Xu O(|update|)dynamic sampling (E)static sampling
e v bv Ae G = (V, E) Dynamic Sampling update dynamic sampling algorithm: X ∼ μ dynamic sampling static sampling O˜(|������|) ⟹ O˜(|E|) empty graph (V, ∅) X(0) ∼ ⊕v bv