
Sampling Counting Input:a CSP formula=(V,O,C) Output: .(sampling)almost uniform random satisfying solution .(counting)an estimation of of satisfying solutions exact counting is #P-hard self-reduction Almost Uniform [Jerrum,Valiant,Vazirani 1986] Approximate Sampling adaptive simulated annealing Counting [Stefankovic,Vempala,Vigoda 2009] Application:inference in probabilistic graphical models Gibbs distribution cw=Πc(a) where each c:&g→Ro iEvbl(c) Inference:Pr [X;=IXs =xs] X~u
• exact counting is #P-hard • • Application: inference in probabilistic graphical models Sampling & Counting Input: a CSP formula Output : • (sampling) uniform random satisfying solution • (counting) # of satisfying solutions Φ = (V, Q,C) an estimation of almost Almost Uniform Sampling Approximate Counting self-reduction [Jerrum, Valiant, Vazirani 1986] adaptive simulated annealing [Štefankovič, Vempala, Vigoda 2009] c : i∈ ⨂ 𝗏𝖻𝗅(c) μ Qi → ℝ≥0 (x) ∝ Φ(x) = ∏ c∈C c (x𝗏𝖻𝗅(c)) Inference: Pr X∼μ [Xi = ⋅ ∣ XS = xS] Gibbs where each distribution

Sampling k-SAT Solutions Sampling almost uniform k-SAT solution under LLL-like condition? Mathematics and Computation [Wigderson 2020]: COAFU7A0米 Ar Myeason "the solution space (and hence the natural Markov chain)is not connected" Random walk in solution space (Markov chain Monte Carlo,MCMC): e ere here! Rapid Mixing Slow (Torpid)Mixing Not Mixing
• Sampling almost uniform k-SAT solution under LLL-like condition? • Random walk in solution space (Markov chain Monte Carlo, MCMC): Sampling k-SAT Solutions “the solution space (and hence the natural Markov chain) is not connected” Mathematics and Computation [Wigderson 2020]: Rapid Mixing Slow (Torpid) Mixing Not Mixing We ere here!
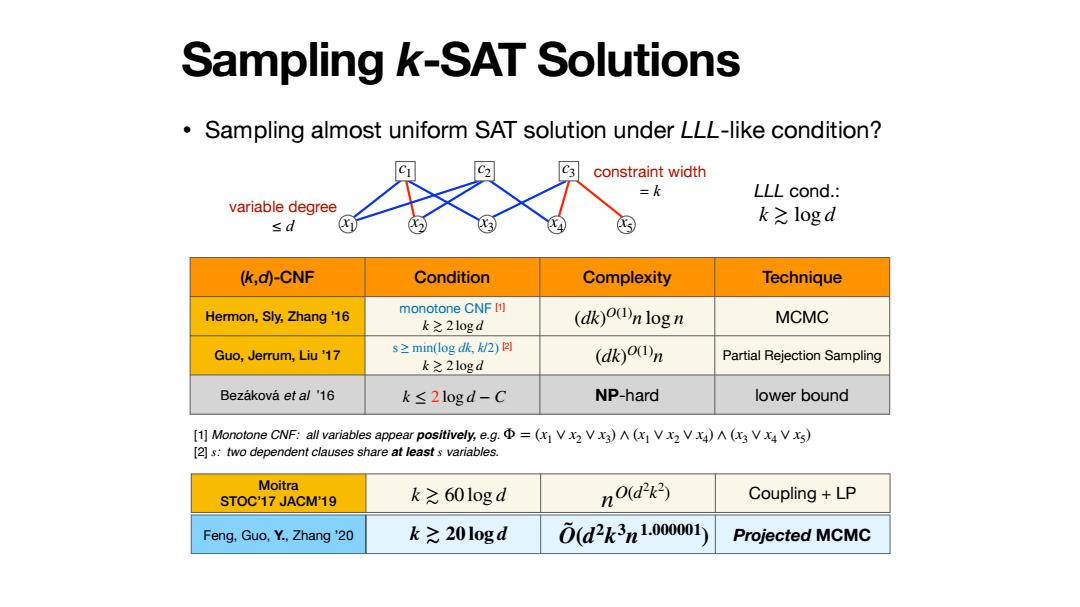
Sampling k-SAT Solutions Sampling almost uniform SAT solution under LLL-like condition? constraint width =k LLL cond.: variable degree sd k之logd (k,d)-CNF Condition Complexity Technique Hermon,Sly,Zhang'16 monotone CNF [1] k之21ogd (dk)o(n log n MCMC Guo,Jerrum,Liu'17 s≥min(log dk/2)☒ (dk)o(n Partial Rejection Sampling k之21ogd Bezakova et al '16 k≤2logd-C NP-hard lower bound [1]Monotone CNF:all variables appear positively,e.g.=(x V2 VX)(x VX2Vx)A (x3 Vx V xs) [2]s:two dependent clauses share at least s variables. Moitra STOC'17 JACM'19 k之60logd nO(dk) Coupling LP Feng,Guo,Y.,Zhang'20 k之20logd 0(d2k3n1.000001 Projected MCMC
• Sampling almost uniform SAT solution under LLL-like condition? Sampling k-SAT Solutions (k,d)-CNF Condition Complexity Technique Hermon, Sly, Zhang ’16 monotone CNF [1] MCMC Guo, Jerrum, Liu ’17 s ≥ min(log dk, k/2) [2] Partial Rejection Sampling Bezáková et al ’16 NP-hard lower bound k ≳ 2 log d (dk) O(1) n log n k ≳ 2 log d (dk) O(1) n k ≤ 2 log d − C [1] Monotone CNF: all variables appear positively, e.g. [2] s: two dependent clauses share at least 𝑠 variables. Φ = (x1 ∨ x2 ∨ x3) ∧ (x1 ∨ x2 ∨ x4) ∧ (x3 ∨ x4 ∨ x5) Moitra STOC’17 JACM’19 k ≳ 60 log d Coupling + LP nO(d2 k2 ) Feng, Guo, Y., Zhang ’20 k ≳ 20 log d O ˜ (d2k3 n1.000001) Projected MCMC c1 c2 c3 x1 x2 x3 x4 x5 constraint width = k variable degree ≤ d LLL cond.: k ≳ log d

Main Theorem (for CNF) [Feng,Guo,Y.,Zhang '20] For any sufficiently small 2-20,any (k,d)-CNF satisfying k≥201ogd+201ogk+31o 1 。Sampling algorithm: draw almost uniform SAT solution in time (d23+5) ·Counting algorithm: count SAT solutions approximately in time (d2k3n2+5)
Main Theorem (for CNF) For any sufficiently small , any (k,d)-CNF satisfying • Sampling algorithm: draw almost uniform SAT solution in time • Counting algorithm: count # SAT solutions approximately in time ζ ≤ 2−20 k ≥ 20 log d + 20 log k + 3 log 1 ζ O ˜ (d2 k3 n1+ζ ) O ˜ (d2 k3 n2+ζ ) [Feng, Guo, Y., Zhang ’20]
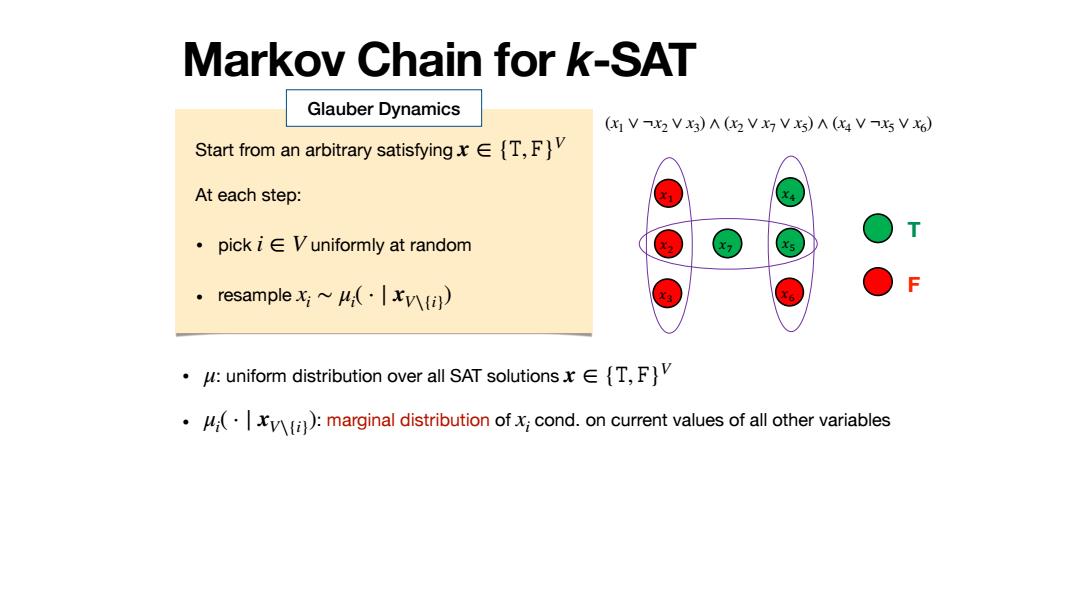
Markov Chain for k-SAT Glauber Dynamics (X]VX2VX3)A(VXV x5)A (x4 Vx5VX6) Start from an arbitrary satisfyingx[T,F)V At each step: ·pick i∈V uniformly at random resamplex~以(·|x) A:uniform distribution over all SAT solutionsx[T,F]V .(marginal distribution ofcond.on current values of all other variables
Markov Chain for k-SAT Start from an arbitrary satisfying At each step: • pick uniformly at random • resample x ∈ {𝚃, 𝙵}V i ∈ V xi ∼ μi ( ⋅ ∣ xV∖{i}) !" !# !$ !% !& !' !( (x1 ∨ ¬x2 ∨ x3) ∧ (x2 ∨ x7 ∨ x5) ∧ (x4 ∨ ¬x5 ∨ x6) T F • : uniform distribution over all SAT solutions • : marginal distribution of cond. on current values of all other variables μ x ∈ {𝚃, 𝙵}V μi ( ⋅ ∣ xV∖{i}) xi Glauber Dynamics