
SHONAN 别 NII MEETING Distributed Algorithms MCMp for Yitong Yin Nanjing University Shonan Meeting No.162:Distributed Graph Algorithms
Distributed Algorithms for MCMC Sampling Yitong Yin Nanjing University Shonan Meeting No. 162: Distributed Graph Algorithms

Outline Distributed Sampling Problem Gibbs Distribution (distribution defined by local constraints) Algorithmic ldeas CLocal Metropolis Algorithm LOCAL Jerrum-Valiant-Vazirani Local Rejection Sampling MCMC Distributed Simulation of Metropolis (with ideal parallelism) MCMC:Markoy chain Monte Carlo
Outline • Distributed Sampling Problem • Gibbs Distribution (distribution defined by local constraints) • Algorithmic Ideas • Local Metropolis Algorithm • LOCAL Jerrum-Valiant-Vazirani • Local Rejection Sampling • Distributed Simulation of Metropolis (with ideal parallelism) MCMC MCMC MCMC: Markov chain Monte Carlo
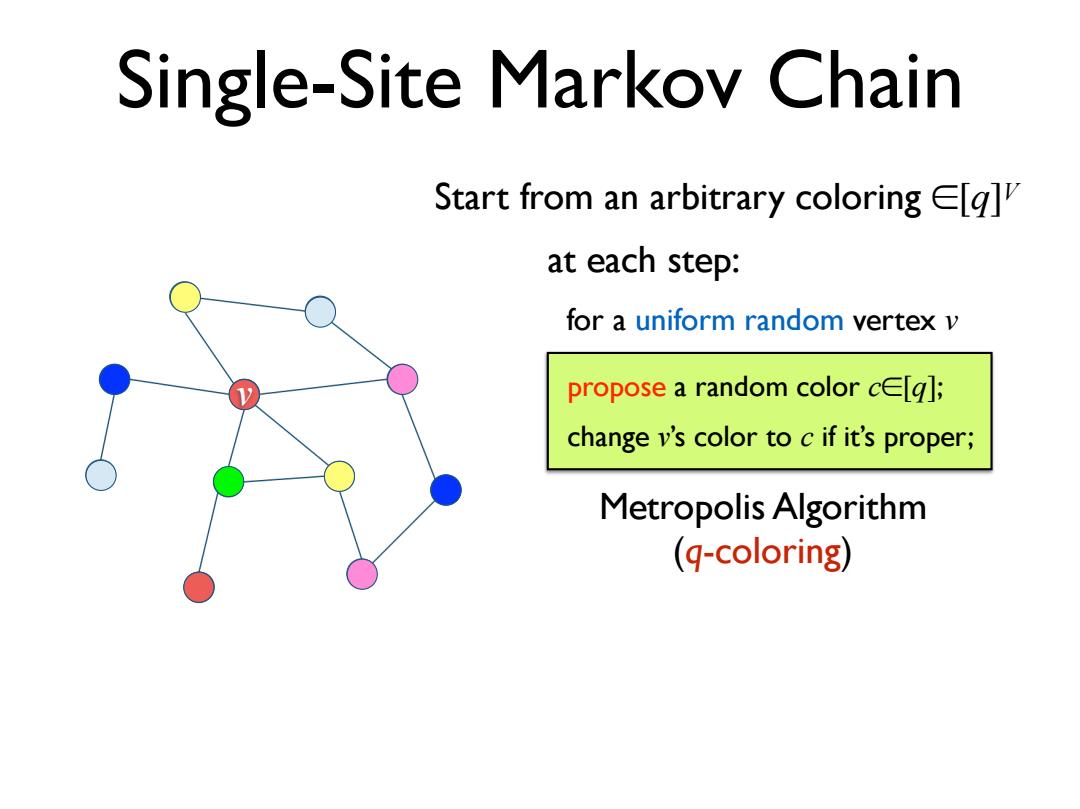
Single-Site Markov Chain Start from an arbitrary coloring Elg] at each step: for a uniform random vertex v propose a random color cE[g]; change v's color to c if it's proper; Metropolis Algorithm (q-coloring)
Single-Site Markov Chain v propose a random color c∈[q]; change v’s color to c if it’s proper; at each step: Metropolis Algorithm (q-coloring) for a uniform random vertex v Start from an arbitrary coloring ∈[q]V
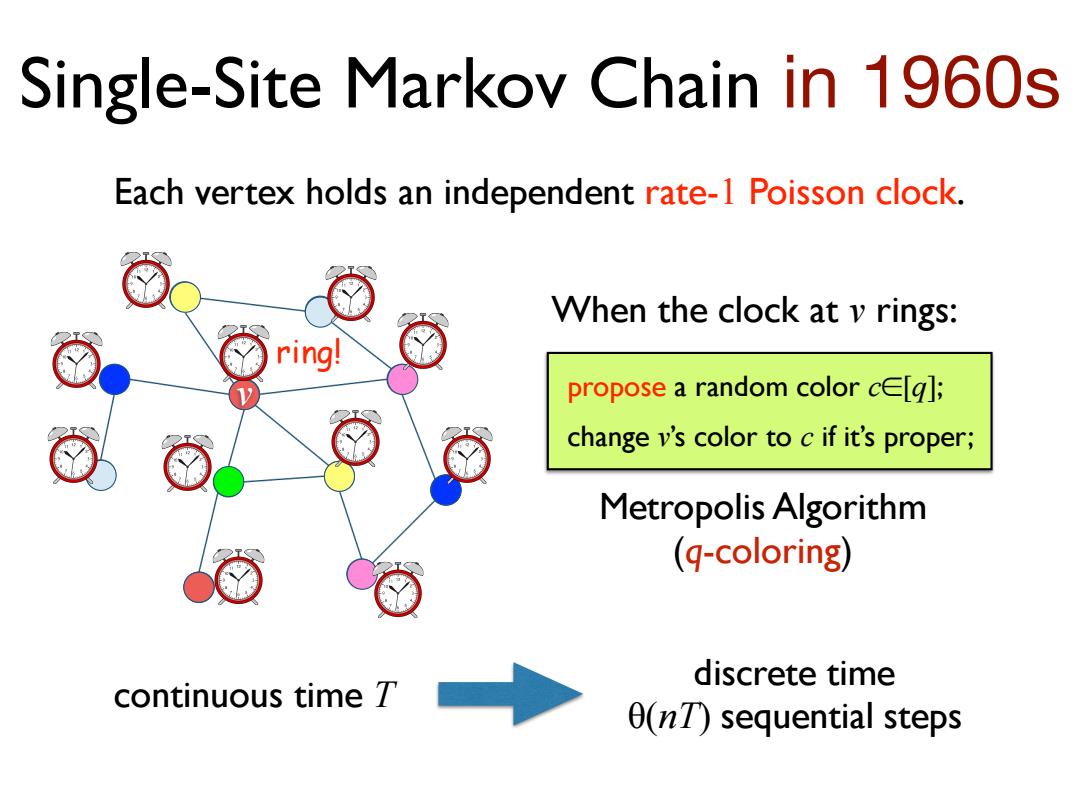
Single-Site Markov Chain in 1960s Each vertex holds an independent rate-1 Poisson clock. When the clock at v rings: ring! propose a random color ce[g]; change v's color to c if it's proper; Metropolis Algorithm (q-coloring) discrete time continuous time 7 0(nT)sequential steps
v propose a random color c∈[q]; change v’s color to c if it’s proper; Metropolis Algorithm (q-coloring) Single-Site Markov Chain in 1960s Each vertex holds an independent rate-1 Poisson clock. When the clock at v rings: continuous time T discrete time θ(nT) sequential steps ring!

Distributed Simulation of Continuous-Time Process Goal:Give a distributed algorithm that perfect simulates the time T continuous Markoy chain. (Have the same behavior given the same random bits.) do NOT allow adjacent vertices update their colors in the same round: O(7)rounds [Feng,Hayes,Y.'19]: O(T+log n)rounds w.h.p. (under some mild condition)
Distributed Simulation of Continuous-Time Process Goal: Give a distributed algorithm that perfect simulates the time T continuous Markov chain. (Have the same behavior given the same random bits.) do NOT allow adjacent vertices update their colors in the same round: O(ΔT) rounds [Feng, Hayes, Y. ’19]: O(T + log n) rounds w.h.p. (under some mild condition)