
Local Distributed Sampling from Locally-Defined Distribution Yitong Yin Nanjing University
Local Distributed Sampling !om Locally-Defined Distribution Yitong Yin Nanjing University

Counting and Sampling RANDOM GENERATION OF COMBINATORIAL STRUCTURES FROM A UNIFORM DISTRIBUTION LGORITHMS Mark R.JERRUM Department f Computer Science,Universiry of Edinburgh,Edinburgh EH93 Unied Kingdom Leslie G.VALIANT* Aiken Computation Laboratory,Harard Universiry,Cambridge,MA 02138,U.S.A V灯jayV.VAZIRANI* Computer Scence Department,Comell Universiry,Ithac,NY 14853,U.S.A. [Jerrum-Valiant-Vazirani86]: (For self-reducible problems) approx.counting (approx.,exact)sampling is tractable is tractable
Counting and Sampling approx. counting is tractable (approx., exact) sampling is tractable (For self-reducible problems) [Jerrum-Valiant-Vazirani ’86]:

Computational Phase Transition Sampling almost-uniform independent set in graphs with maximum degree△: ●[Weitz2006]:lf△≤5,poly-time. [Sly 2010]:If A=6,no poly-time algorithm unless NP=RP. A phase transition occurs when△:5→6. Local Computation?
Computational Phase Transition • [Weitz 2006]: If ∆≤5, poly-time. • [Sly 2010]: If ∆≥6, no poly-time algorithm unless NP=RP. Sampling almost-uniform independent set in graphs with maximum degree ∆: A phase transition occurs when ∆: 5→6. Local Computation?
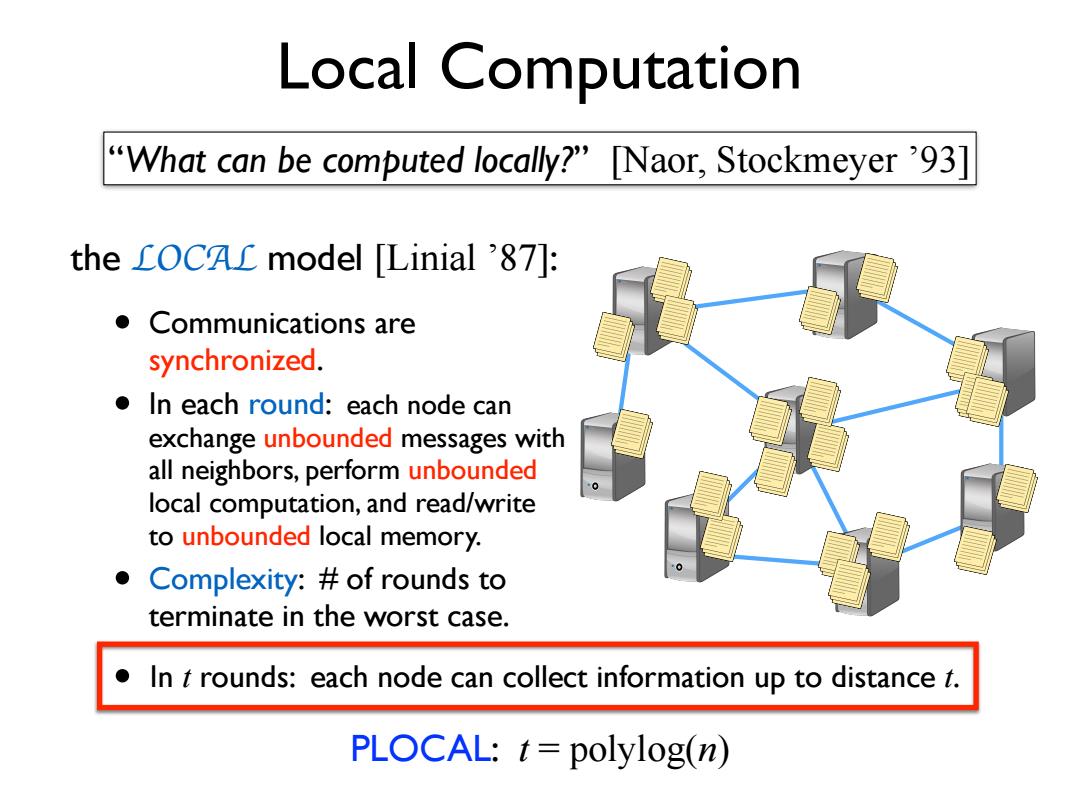
Local Computation "What can be computed locally?"[Naor,Stockmeyer'93] the LOCAC model [Linial '87]: Communications are synchronized. In each round:each node can exchange unbounded messages with all neighbors,perform unbounded local computation,and read/write to unbounded local memory. Complexity:of rounds to terminate in the worst case. In t rounds:each node can collect information up to distance t. PLOCAL:t=polylog(n)
Local Computation • Communications are synchronized. • In each round: each node can exchange unbounded messages with all neighbors, perform unbounded local computation, and read/write to unbounded local memory. • Complexity: # of rounds to terminate in the worst case. • In t rounds: each node can collect information up to distance t. the LOCAL model [Linial ’87]: “What can be computed locally?” [Naor, Stockmeyer ’93] PLOCAL: t = polylog(n)
A Motivation: Distributed Machine Learning ●Data are stored in a distributed system. Distributed algorithms for: sampling from a joint distribution(specified by a probabilistic graphical model); ● inferring according to a probabilistic graphical model
A Motivation: Distributed Machine Learning • Data are stored in a distributed system. • Distributed algorithms for: • sampling from a joint distribution (specified by a probabilistic graphical model); • inferring according to a probabilistic graphical model