
东北财经大学职业枝术学院 第七章投资决策 第一节投资决策基础理论 气之件终然装值味 通用的利息计算方法规定,利息的计算间隔期与利率的间隔期应该一 及务车等 贷款额称为本金,贷款额 设B表示本金 I表示利率 n表示结算利息的期数F表示终值 当n=1F1=B(1+i) 当n-2 F2=B(1+i)2 当n=3F3=B(1+i)3 当nm Fn=B (1+i)n 或简写成FB(1+i)n(终值公式)
三、终值公式与终值表 (一)终值公式 通用的利息计算方法规定,利息的计算间隔期与利率的间隔期应该一 致。如每年计算一次利息,其利率应采用年历率,贷款额称为本金,贷款额 及利息之和称为“终值”,俗称“本利和”。终值的计算公式如下: 设 B表示本金 I表示利率 n表示结算利息的期数 F表示终值 当n=1 F1= B(1+i) 当n=2 F2= B(1+i)2 当n=3 F3= B(1+i)3 当n=n Fn= B(1+i)n 或简写成F= B(1+i)n (终值公式) 第七章 投资决策 第一节 投资决策基础理论

化纹子 东北财经大学职业枝术学院 第七章投资决策 第一节投资决策基础理论 (二)终值表: 为了便利日常的利息计算工作,前人已设计并编出一种终值计算表 表的横向按利率由小到大,顺序排列 纵向接结算利息的期数自少至多,顺序排列 本金接货币单位“一元”计算,此计算标准称为“终值表”或称 (1+i)n表 例:计算贷款为1000元,利率为10%,期数为5的终值。 查终值表可得(1+i)6=1.610 代入终值公式可得F=1000×1.61=1610元
(二)终值表: 为了便利日常的利息计算工作,前人已设计并编出一种终值计算表。 表的横向按利率由小到大,顺序排列 纵向接结算利息的期数自少至多,顺序排列 本金接货币单位“一元”计算,此计算标准称为“终值表”或称 (1+i)n表 例:计算贷款为1000元,利率为10%,期数为5的终值。 查终值表可得(1+i)5 =1.610 代入终值公式可得 F=1000×1.61=1610元 第七章 投资决策 第一节 投资决策基础理论
东北财经大学职业枝术学院 第七章投资决策 第一节投资决策基础理论 (三)终值公式与终值表的应用 终值公式与终值表除用语计算终值外,还可以反算利率, 计算莉息的期数以及其它经济方面的问题。 例1:国民经济在二十年中翻两番,其平均每年增长速度 为多少? 本例计算式应该是(1+i)20=4 查表可得:当i=7时(1+0.07)20=3.869 i=? 4 i=8时(1+0.08)20=4.660 采用插入比例法计算平均每年的增长速度 .i=0.07166
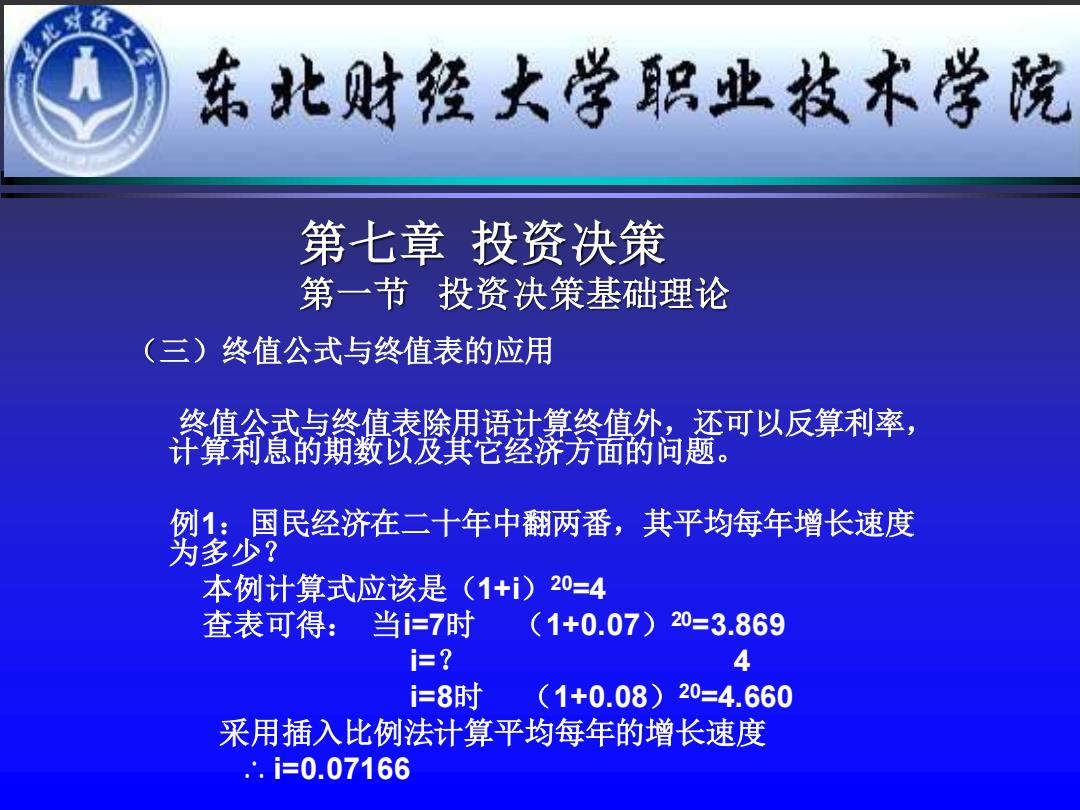
(三)终值公式与终值表的应用 终值公式与终值表除用语计算终值外,还可以反算利率, 计算利息的期数以及其它经济方面的问题。 例1:国民经济在二十年中翻两番,其平均每年增长速度 为多少? 本例计算式应该是(1+i)20=4 查表可得: 当i=7时 (1+0.07)20=3.869 i=? 4 i=8时 (1+0.08)20=4.660 采用插入比例法计算平均每年的增长速度 ∴ i=0.07166 第七章 投资决策 第一节 投资决策基础理论
东北财经大学职业枝术学院 第七章投资决策 第一节投资决策基础理论 例2:某工厂以每年增长10%速度发展,试问该企业几年以 后可以翻两番? 本例的计算公式应该是(1+0.1)=4 查终值表:n=14(1+0.1)14=3.797 n=? 4 n=15 (1+0.1)15=4.177 ,.n=14+ 4-37%1=14.534(年) 4.177-3.797 近似地说,该工厂每年递增10%,需15年才能翻两番
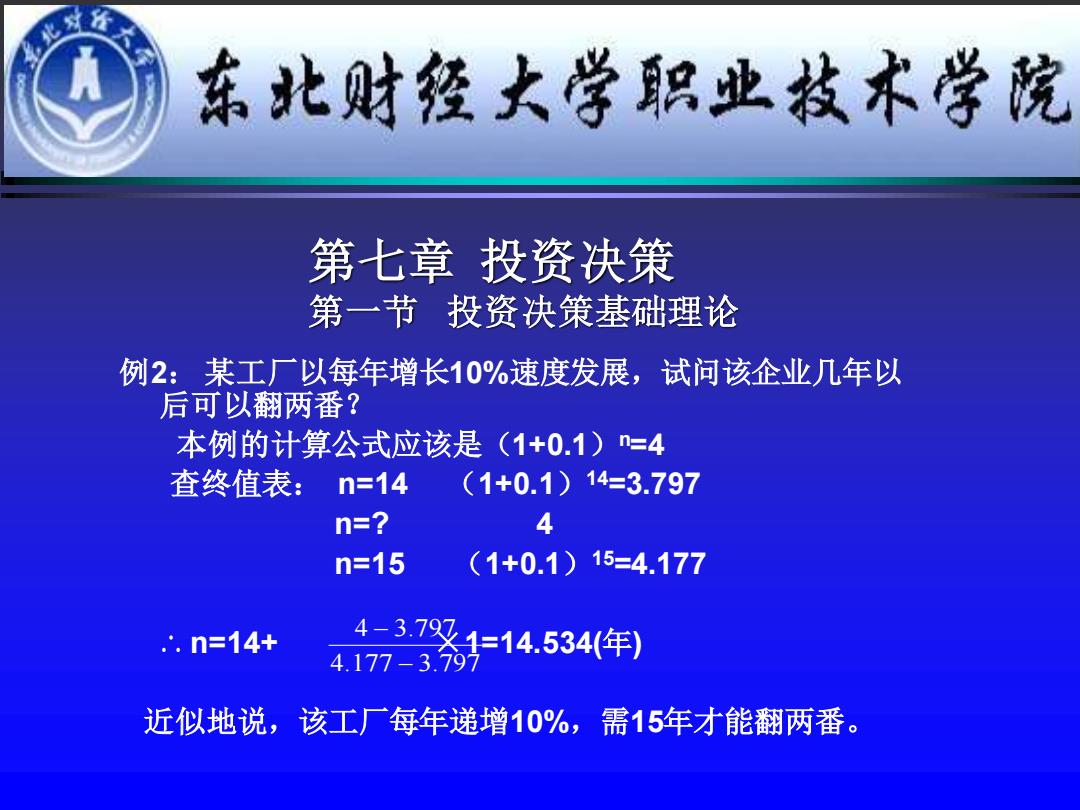
例2: 某工厂以每年增长10%速度发展,试问该企业几年以 后可以翻两番? 本例的计算公式应该是(1+0.1)n=4 查终值表: n=14 (1+0.1)14=3.797 n=? 4 n=15 (1+0.1)15=4.177 ∴ n=14+ ×1=14.534(年) 近似地说,该工厂每年递增10%,需15年才能翻两番。 4.177 3.797 4 3.797 − − 第七章 投资决策 第一节 投资决策基础理论

东北财经大学职业技术学院 第七章投资决策 第一节投资决策基础理论 例3:设本金1000元,月利率为1%,十三年后 的终值为多少元? 终值F=1000×(1+0.01)12×12 =1000×(1+0.01)100 (1+0.01)44 =4188.50(元)
例3:设本金1000元,月利率为1%,十三年后 的终值为多少元? 终值F=1000×(1+0.01)12×12 =1000×(1+0.01)100 (1+0.01)44 =4188.50(元) 第七章 投资决策 第一节 投资决策基础理论