电子科技大学：《现代网络理论与综合 Theory and Synthesize of Electric Network》研究生课程教学资源（课件讲稿）第6讲 网络函数拓扑法

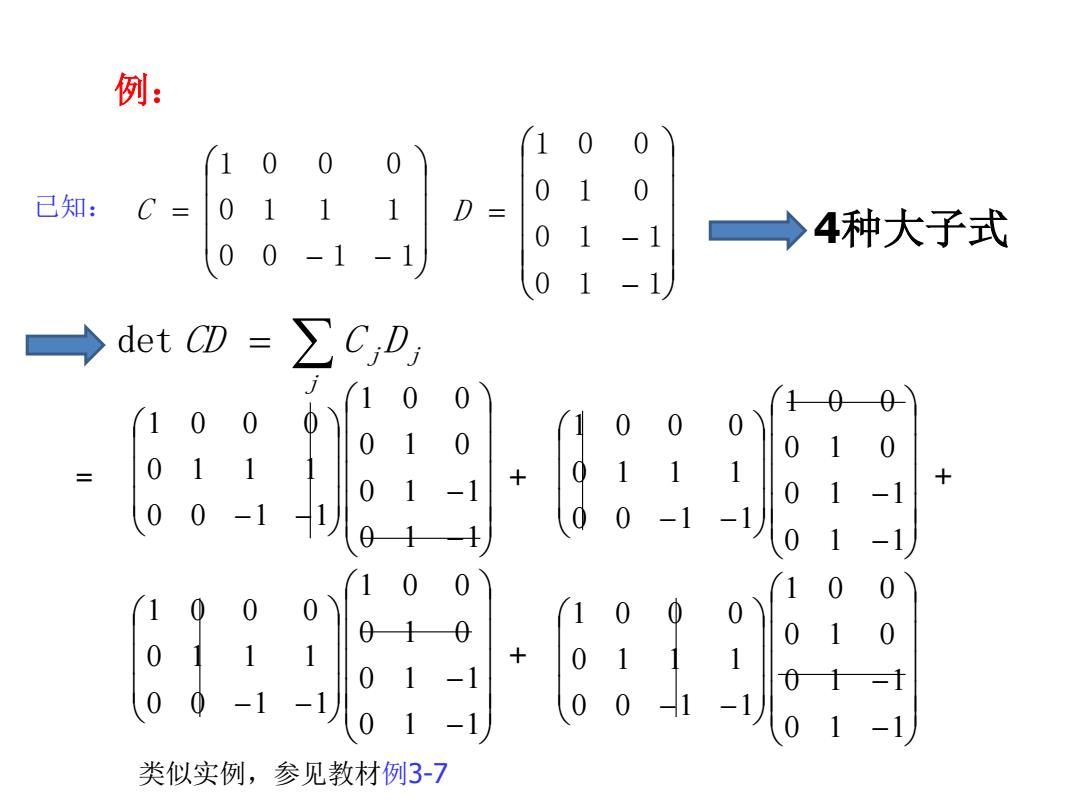
例： 10 01 0 已知： C= 1 1 0 -1 →4种大子式 → det D=∑C,D, 0。-1刀 10 0 01 1 10 0→ 类似实例，参见教材例3-7

例：              0 0 1 1 0 1 1 1 1 0 0 0 C                  0 1 1 0 1 1 0 1 0 1 0 0 D 4种大子式           0 0 1 1 0 1 1 1 1 0 0 0                 0 1 1 0 1 1 0 1 0 1 0 0           0 0 1 1 0 1 1 1 1 0 0 0                 0 1 1 0 1 1 0 1 0 1 0 0           0 0 1 1 0 1 1 1 1 0 0 0                 0 1 1 0 1 1 0 1 0 1 0 0           0 0 1 1 0 1 1 1 1 0 0 0                 0 1 1 0 1 1 0 1 0 1 0 0 + + + = 已知：   j det CD C j D j 类似实例，参见教材例3-7

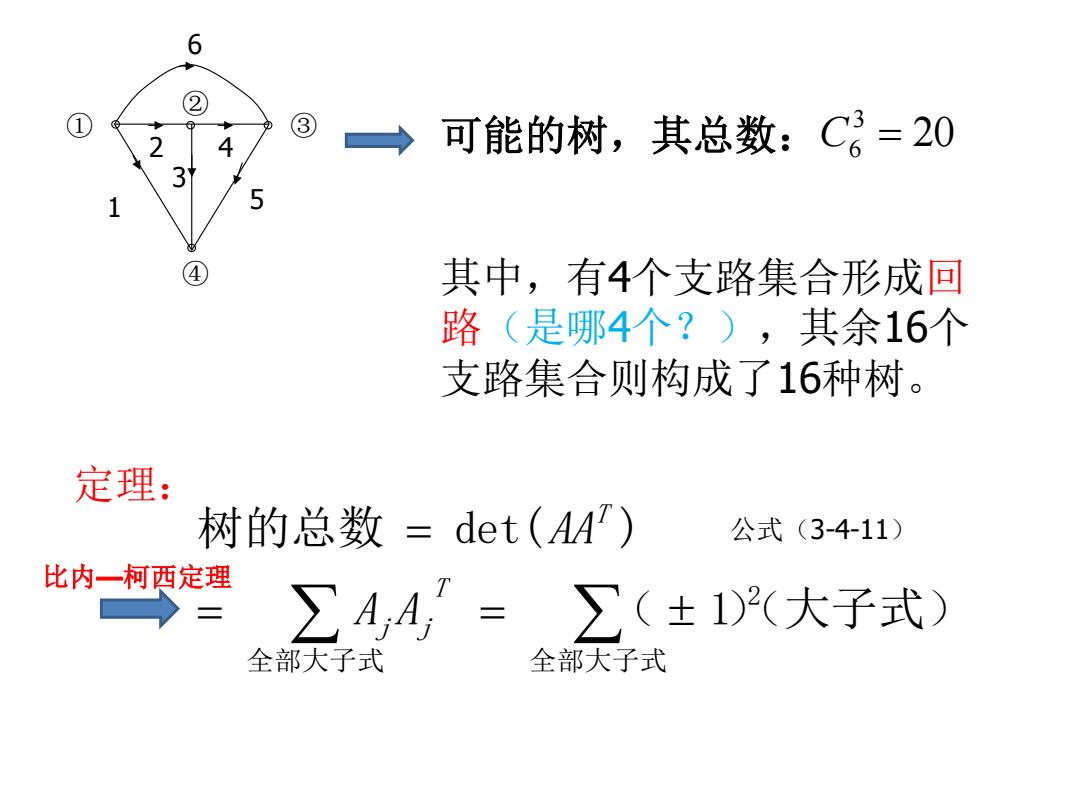
6 2 ③ 可能的树，其总数：C3=20 5 ④ 其中，有4个支路集合形成回 路（是哪4个？），其余16个 支路集合则构成了16种树。 定理： 树的总数=det(AA) 公式(3-4-11〉 比内一柯西定理 ∑AA=∑（±1D(大子式） 全部大子式 全部大子式

① ② ③ ④ 1 2 3 4 5 6 可能的树，其总数：       全部大子式 2 全部大子式 （ 1）（大子式） 树的总数 det( ) T j j T A A AA 20 3 C6  其中，有4个支路集合形成回 路（是哪4个？），其余16个 支路集合则构成了16种树。 定理： 公式（3-4-11） 比内—柯西定理

6 例： ② ③ 4 3 1 5 ④ 树总数=det(AA) 直接计算： 1 0 110 0 0 1 3 -1-1 0 0 =det0-11 0 0 =det-13-1 =16 000-11-1 -1-13

① ② ③ ④ 1 2 3 4 5 6 1 6 1 1 3 1 3 1 3 1 1 det 1 0 1 0 0 1 0 1 1 0 1 0 1 1 0 1 0 0 0 0 0 1 1 1 0 1 1 1 0 0 1 1 0 0 0 1 det det( )                   T 树总数 AA 例： 直接计算 ：

已知：无源，无互感，RLC单口线性无源网络 6 →△=dety ② Y =AYA' ③ 2 4 △=det y.=det AY,4 1 5 ④ 已知： 110 001 Yb对角阵 A= 0 -1 00 A与AY,同构 000-11-1 Y 11 0001 Y AY= 0-1 1 10 00 0-11-1 Y6)

① ② ③ ④ 1 2 3 4 5 6               0 0 0 1 1 1 0 1 1 1 0 0 1 1 0 0 0 1 A                                   6 5 4 3 2 1 0 0 0 1 1 1 0 1 1 1 0 0 1 1 0 0 0 1 Y Y Y Y Y Y AYb A 与 AYb 同构 已知：无源，无互感，RLC单口线性无源网络 T n b T n b n Y AY A Y AY A Y det det det       已知： 对角阵

6 ② ③ 4 Y Y 0 0 0 Yo 3 1 5 AY= 0 -Y2 Y3 Y 0 0 0 00 -Y4 Ys -Y6 ④ 1 0 0 1 -1 0 0 1 A= 019988 AT 00-11-1 0 1 0 0 0 A与AY,同构 1

① ② ③ ④ 1 2 3 4 5 6       4 5 6 2 3 4 1 2 6 0 0 0 0 0 0 0 0 0 Y Y Y Y Y Y Y Y Y AYb       0 0 0 1 1 1 0 1 1 1 0 0 1 1 0 0 0 1 AA 与 AYb 同构      1 0 1 0 0 1 0 1 1 0 1 0 1 1 0 1 0 0 T A