
度为n-2=31-2=29的临界值4(29)=2.045.因为(B)=0,982520<1(29)=2.045 所以不能拒绝H:B=0;因为(B,)=20,54026>6(29)=2045,所以应拒绝H,B=0, 这表明,城市人均年可支配收入对人均年消费支出有显著影响。 五、回归预测 由表2.5中可看出,2002年中国西部地区城市居民人均年可支配收入除了西藏外均在 8000以下,人均消费支出也都在7000元以下。在西部大开发的推动下,如果西部地区的 城市居民人均年可支配收入第一步争取达到1000美元(按现有汇率即人民币8270元),第 二步再争取达到1500美元(即人民币12405元),利用所估计的模型可预测这时城市居民可 能达到的人均年消费支出水平。可以注意到,这里的预测是利用截面数据模型对被解释变 量在不同空间状况的空间预测。 用EViews作回归预测,首先在“Workfile”窗口点击“Range”,出现“Change Workfile Range”窗口,将“End data”由“31”改为“33”,点“oK”,将Workfile”中的“Range 扩展为1-33.在“Workfile”窗口点击“sapl”,将“samp"窗口中的“131”改为“133” 点“0K”,将样本区也改为1一33. 为了输入Xn=8270,Xn=l2405在EVicws命今框键入data×/但车,在X数据表 中的“32”位置输入“8270,在“33”的位置输入“12405”,将数据表最小化. 然后在“Equation”柜中,点击“Forecast”,得对话柜。在对话柜中的“Forecast name' (倾测值序列名)键入,回车即得到模型估计值及标准误差的图形。双击“Wkfi1。 窗口中出现的W,在,裁据表中的“32位置出现预测值'n=655132,在33 位置出现'n=9691.577.这是当Xn=8270和Xn=12405时人均消费支出的,点预测值, 为了作区间预测,在X和Y的效据表中,点击“View”选“Descriptive Stats\Cmmon Sample'”,则得到X和Y的描述统计结果,见表2.7: 15
15 度为n - 2 = 31- = 2 29的临界值 0.025 t (29) = 2.045 。因为 ^ 1 0.025 t t (b ) = 0.982520 < = (29) 2.045 , 所以不能拒绝 0 1 H : 0 b = ;因为 ^ 2 0.025 t t ( ) b = 20.54026 > = (29) 2.045,所以应拒绝 0 2 H : 0 b = 。 这表明,城市人均年可支配收入对人均年消费支出有显著影响。 五、回归预测 由表 2.5 中可看出,2002 年中国西部地区城市居民人均年可支配收入除了西藏外均在 8000 以下,人均消费支出也都在 7000 元以下。在西部大开发的推动下,如果西部地区的 城市居民人均年可支配收入第一步争取达到 1000 美元(按现有汇率即人民币 8270 元),第 二步再争取达到 1500 美元(即人民币 12405 元),利用所估计的模型可预测这时城市居民可 能达到的人均年消费支出水平。可以注意到,这里的预测是利用截面数据模型对被解释变 量在不同空间状况的空间预测。 用 EViews 作回归预测,首先在“Workfile”窗口点击“Range”,出现“Change Workfile Range”窗口,将“End data”由“31”改为“33”,点“OK”,将“Workfile”中的“Range” 扩展为 1—33。在“Workfile”窗口点击“sampl”,将“sampl”窗口中的“1 31”改为“1 33”, 点“OK”,将样本区也改为 1—33。 为了输入 1 8270 X f = , 2 12405 X f = 在 EViews 命令框键入 data x /回车, 在 X 数据表 中的“32”位置输入“8270”,在“33”的位置输入“12405”,将数据表最小化。 然后在“E quation”框中,点击“Forecast”,得对话框。在对话框中的“Forecast name” (预测值序列名)键入“ Yf ”, 回车即得到模型估计值及标准误差的图形。双击“Workfile” 窗口中出现的“Yf ”,在“Yf ”数据表中的“32”位置出现预测值 1 6555.132 Yf = ,在“33” 位置出现 2 9691.577 Yf = 。这是当 1 8270 X f = 和 2 12405 X f = 时人均消费支出的点预测值。 为了作区间预测,在 X 和 Y 的数据表中,点击“View”选“Descriptive Stats\Cmmon Sample”,则得到 X 和 Y 的描述统计结果,见表 2.7:

Mean 7515.0265982.4761 an 表2.7 5234.3504462080 Std.Dev. 2042.6821601.762 45045 4.767999 Observations 3131 根据表2.7的数据可计算: ∑x=o2(n-1)=2042.6822×(31-1)=125176492.59 (Xn-X)3=(8270-7515.0269=569985.74 (X2-Xy2=12405-7515.026)2=23911845.72 取a=0.05,'平均值置信度95%的预测区间为: Vn∑ 1.569985.74 Xn=8270时 655.13年2.045x413.1593×+2517649259 =6555.13年162.10 X2=12405时 w5r20as4B16 =9691.58年499.25 即是说,当Xn=8270元时,'n平均值置信度5%的预测区间为(6393.03,6717.23) 元.当Xn=12405元时,'n平均值置信度95%的预测区间为(9292.33,10090.83)元. y个别值置信度95%的预测区间为: +1(X-) YtheG+n+∑
16 表 2.7 根据表 2.7 的数据可计算: 2 2 2 ( 1) 2042.682 (31 1) 125176492.59 i x åx n =s - = ´ - = 2 2 1 (X X f - ) = (8270 - = 7515.026) 569985.74 2 2 2 (X X f - ) = (12405- = 7515.026) 23911845.72 取a = 0.05, Yf 平均值置信度 95%的预测区间为: 2 ^ ^ 2 2 1 ( ) f f i X X Y t n x a s - + å m 1 8270 X f = 时 1 569985.74 6555.13 2.045 413.1593 31 125176492.59 m ´ ´ + = 6555.13m162.10 2 12405 X f = 时 1 23911845.72 9691.58 2.045 413.1593 31 125176492.59 m ´ ´ + = 9691.58m 499.25 即是说,当 1 8270 X f = 元时, Yf 1平均值置信度 95%的预测区间为(6393.03,6717.23) 元。当 2 12405 X f = 元时, Yf 2平均值置信度 95%的预测区间为(9292.33,10090.83)元。 Yf 个别值置信度 95%的预测区间为: 2 ^ ^ 2 2 1 ( ) 1 f f i X X Y t n x a s - + + å m
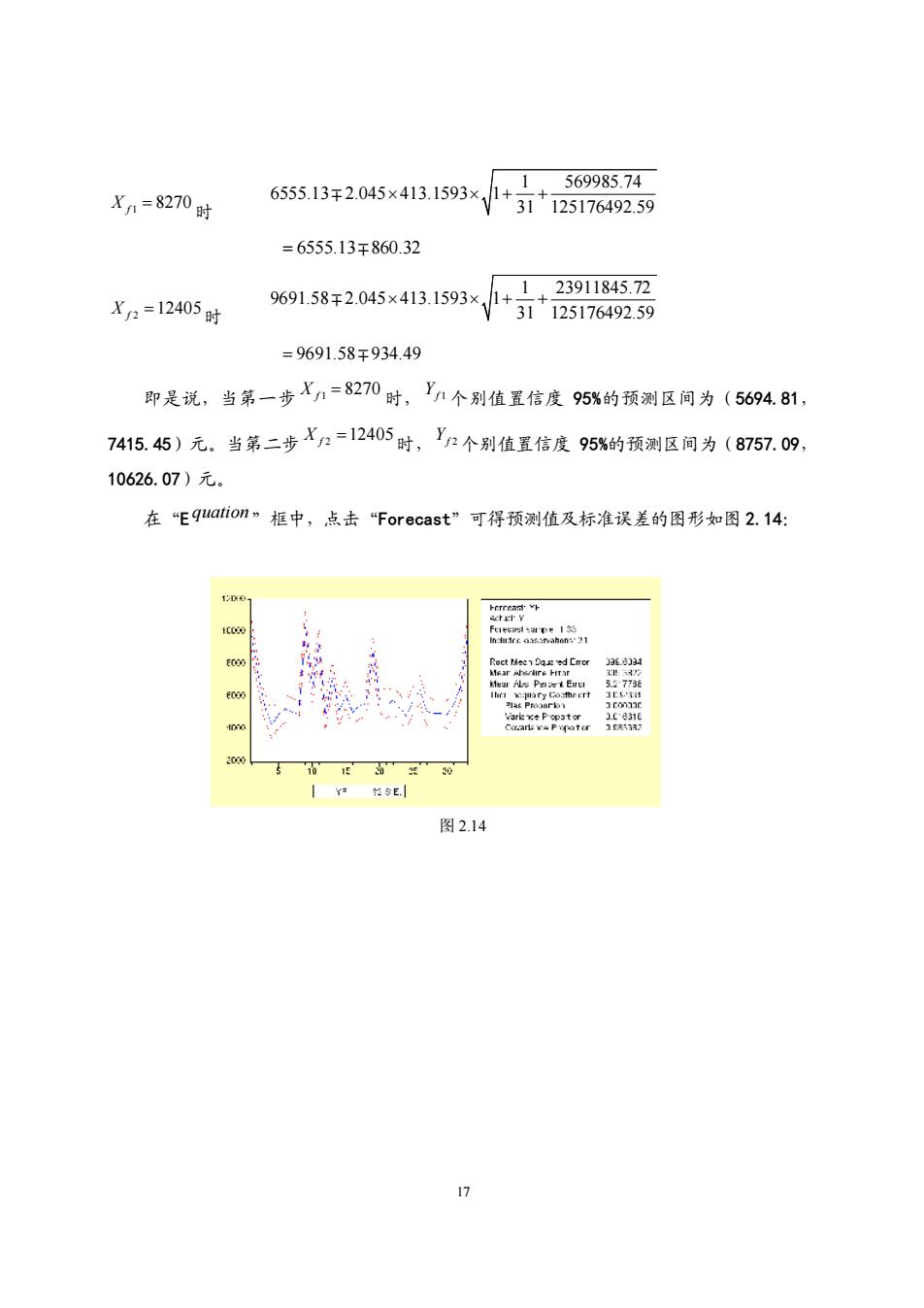
Xn=8270时 655.13年2045×413.1593×,++5698574 31125176492.59 =6555.13年860.32 23911845.72 X2=12405时 969158干2045×4131593xy+写7+282 =9691.58干934.49 即是说,当第一步Xn=8270时,V1个别值置信度95%的预测区间为(569481, 7415.45)元.当第二步Xn=12405时,V个别值置信度95%的预测区间为(8757.09。 10626.07)元. 在“E9uai0n”框中,点击Forecast'”可得预测值及标准误差的图形如图2.14: 图2.14
17 1 8270 X f = 时 1 569985.74 6555.13 2.045 413.1593 1 31 125176492.59 m ´ ´ + + = 6555.13m 860.32 2 12405 X f = 时 1 23911845.72 9691.58 2.045 413.1593 1 31 125176492.59 m ´ ´ + + = 9691.58m 934.49 即是说,当第一步 1 8270 X f = 时, Yf 1 个别值置信度 95%的预测区间为(5694.81, 7415.45)元。当第二步 2 12405 X f = 时, Yf 2 个别值置信度 95%的预测区间为(8757.09, 10626.07)元。 在“E quation”框中,点击“Forecast”可得预测值及标准误差的图形如图 2.14: 图 2.14