
据人Store(将数据存储到磁盘人Delete(删除)对象。此外,可以从工作文件目录中选 取并双击对象,用户就可以展示和分析工作文件内的任何数据。工作文件一开始其中就包 含了两个对象,一个是系数序列C(保存估计系数用),另一个残差序列ESD(实际值与 拟合值之差)。小图标上标识出对象的类型,C是系数向量,曲线图是时间序列。用户选择 Vi©ws对象后双击鼠标左建或直接使用EViews主窗口项部的菜单选项,可以对工作文件和 其中的对象进行 一些处理 4、保存工作成果:将工作成果保存到磁盘,点击工具条中 引输入文件名、路 径\保存, ,或,点击菜单栏中File1Save或Save as\输入文件名 5、打开工作文件:我们可以打开一个已有的工作文件继续以前的工作,点击主莱单 中的File10pen\Workfile\选定文件\打开. 三、输入和编辑数据 建立或调入工作文件以后,可以输入和编辑数据。输入数据有两种基本方法:data 命令方式和鼠标图形界面方式 1、data命今方式:命今格式为:data<序列名1><序列名2> 《序利l名n>.序 列名之问用空格隔开 输入全部序列后回车就进入据编辑窗口, 如图五所示。用月 按照Excel 的数 据输入习惯输 数据输入完毕,可 以关闭数据输入窗口,点击工 作文件雷口工具条的Save或,点击菜单栏的File丨Save将数据存入磁盘. 2、鼠标图形界面方式一 一数组方式:点击Quick\Empty Group(Edit Series),进 入数据窗口编辑窗口,点击bs行没有数据的第一列(如图五中太阳标志处),然后输入 序列名,并可以如此输入多个序列。输入数据名后,可以输入数据,方式同上。 3、鼠标图形界面方式 一序列方式:点击Ob iects\New ob iect\选Series\输 入序列名称0k,进入数据编辑窗口,点击Eit+/-打开数据编辑状态,(用户可以根据习惯 点击Sml+/-改变数据按行或列的显示形式,)然后输入数据, 方式同上 输入命令, 数据编辑窗口工具 8a 序列名称 输入的数据 (图五) 4、编辑工作文件中已有的序列:可以按照操作Windows的习惯在工作文件主显
5 据)、Store(将数据存储到磁盘)、Delete(删除)对象。此外,可以从工作文件目录中选 取并双击对象,用户就可以展示和分析工作文件内的任何数据。工作文件一开始其中就包 含了两个对象,一个是系数序列 C(保存估计系数用),另一个残差序列 RESID(实际值与 拟合值之差)。小图标上标识出对象的类型,C 是系数向量,曲线图是时间序列。用户选择 Views 对象后双击鼠标左建或直接使用 EViews 主窗口顶部的菜单选项,可以对工作文件和 其中的对象进行一些处理。 4、保存工作成果:将工作成果保存到磁盘,点击工具条中 save\输入文件名、路 径\保存,或点击菜单栏中 File \Save 或 Save as \输入文件名、路径\保存。 5、打开工作文件:我们可以打开一个已有的工作文件继续以前的工作,点击主菜单 中的 File \Open \ Workfile \选定文件\打开。 三、输入和编辑数据 建立或调入工作文件以后,可以输入和编辑数据。 输入数据有两种基本方法:data 命令方式和鼠标图形界面方式 1、data 命令方式:命令格式为:data <序列名 1> <序列名 2>.<序列名 n>,序 列名之间用空格隔开,输入全部序列后回车就进入数据编辑窗口,如图五所示。用户可以 按照 Excel 的数据输入习惯输入数据。数据输入完毕,可以关闭数据输入窗口,点击工 作文件窗口工具条的 Save 或点击菜单栏的 File \ Save 将数据存入磁盘。 2、鼠标图形界面方式——数组方式:点击 Quick \ Empty Group (Edit Series), 进 入数据窗口编辑窗口,点击 obs 行没有数据的第一列(如图五中太阳标志处),然后输入 序列名,并可以如此输入多个序列。输入数据名后,可以输入数据,方式同上。 3、鼠标图形界面方式——序列方式:点击 Objects \ New object \ 选 Series \ 输 入序列名称\Ok,进入数据编辑窗口,点击 Edit+/-打开数据编辑状态,(用户可以根据习惯 点击 Smpl+/-改变数据按行或列的显示形式,)然后输入数据,方式同上。 4、编辑工作文件中已有的序列:可以按照操作 Windows 的习惯在工作文件主显 输入命令, 数据编辑窗口工具 序列名称 输入的数据 (图五)

示窗口选定一个或多个序列,点击鼠标右健打开一个或多个序列,进入数据编辑状态,可 以修改数据。 四、由组的明客杏看组内席列的数据特征 按下数组窗口(也可以成为数组或数据编辑窗口)工具条上Viws按钮,可以得到组 (图六) 内数据的特征,见图六。具体介绍如下: Group Members可用于增加组中的序列;SpreadSheet以电子数据表的形式显示数 据:Dated Data Table将使时序数据以表的形式显示:Graph以各种图形的形式显示数据 的Mult i Graph以多图的形式显示组中数据:Descriptive Stats给出组中数据的描选 统计量 如均值 方差、偏度、峰度、小B统计量(用 正态性检验 sts of equality. 给出检验组中序列是否 其有同万差 同均值或相同 位数的假设检验结果;Nway/0 ne-way Tabulation.给出数组中序列观测值在某一区间的频数、频率和某一序列是否与组中其他 LZNN B NG: 3900 R. 图七
6 示窗口选定一个或多个序列,点击鼠标右健打开一个或多个序列,进入数据编辑状态,可 以修改数据。 四 、由组的观察查看组内序列的数据特征 按下数组窗口(也可以成为数组或数据编辑窗口)工具条上 Views 按钮,可以得到组 内数据的特征,见图六。具体介绍如下: Group Members 可用于增加组中的序列;SpreadSheet 以电子数据表的形式显示数 据;Dated Data Table 将使时序数据以表的形式显示;Graph 以各种图形的形式显示数据 的;Multi Graph 以多图的形式显示组中数据;Descriptive Stats 给出组中数据的描述 统计量,如均值、方差、偏度、峰度、J-B 统计量(用于正态性检验)等;Tests of equality. 给出检验组中序列是否具有同方差、同均值或相同中位数的假设检验结果;N-way/One-way Tabulation.给出数组中序列观测值在某一区间的频数、频率和某一序列是否与组中其他 (图六) 图七
正 08 图八 序列独立的假设检验结果;Correlations给出数组中序列的相关系数矩阵;Covarianc 给出数组中序列的斜方差矩阵;C0, relogram(1)给出组内第1序列的水平序列及其差分序 列的自相关函数和偏自相关函数: ross C rrelation2)给出组内第1和第2序列的超前 几期和滞后几期值之间的互相关函数: Cointegration Test执行Johanser cointegration协整(或称为共积)检验; Granger Causality检验组内各个配对间的 Granger因果关系;Lable给出数组的名称及修改时间等信息. 五、回归分析一估计消费函数 1、在经济理论指导下,利用软件包的“观察(ViwP功能对数据进行“火力侦察” 观察消费性支出与可支配收入的散,点图(见图七)。依据凯思斯理论,设定理论模型 consum a+b (inc) 2、作普通最小二乘法估计:在主菜单选Quick \Estimate Equations,.进入输入估计 方程对话框,输入待估计方程,选择估计方法一普通最小二乘法,如图八所示。点击O水进 行估计,得到估计方程(1)及其统计检验结果,如图九所示。 conswn-0.794inc+49.82 (1) (30.89) (0.35) 3、利用图九中给出的统计检验结果对模型的可靠性进行统计学检验,由统计结果可以 看出该模型拟合优良,误差项不存在一阶正自相关 利用图九中估计方程显示窗 b t 具条View 可以显示估计方程、估计方程的统 计结果、以图或表的形式显示数据的实际值、预测值和残差。 六、单方程预测
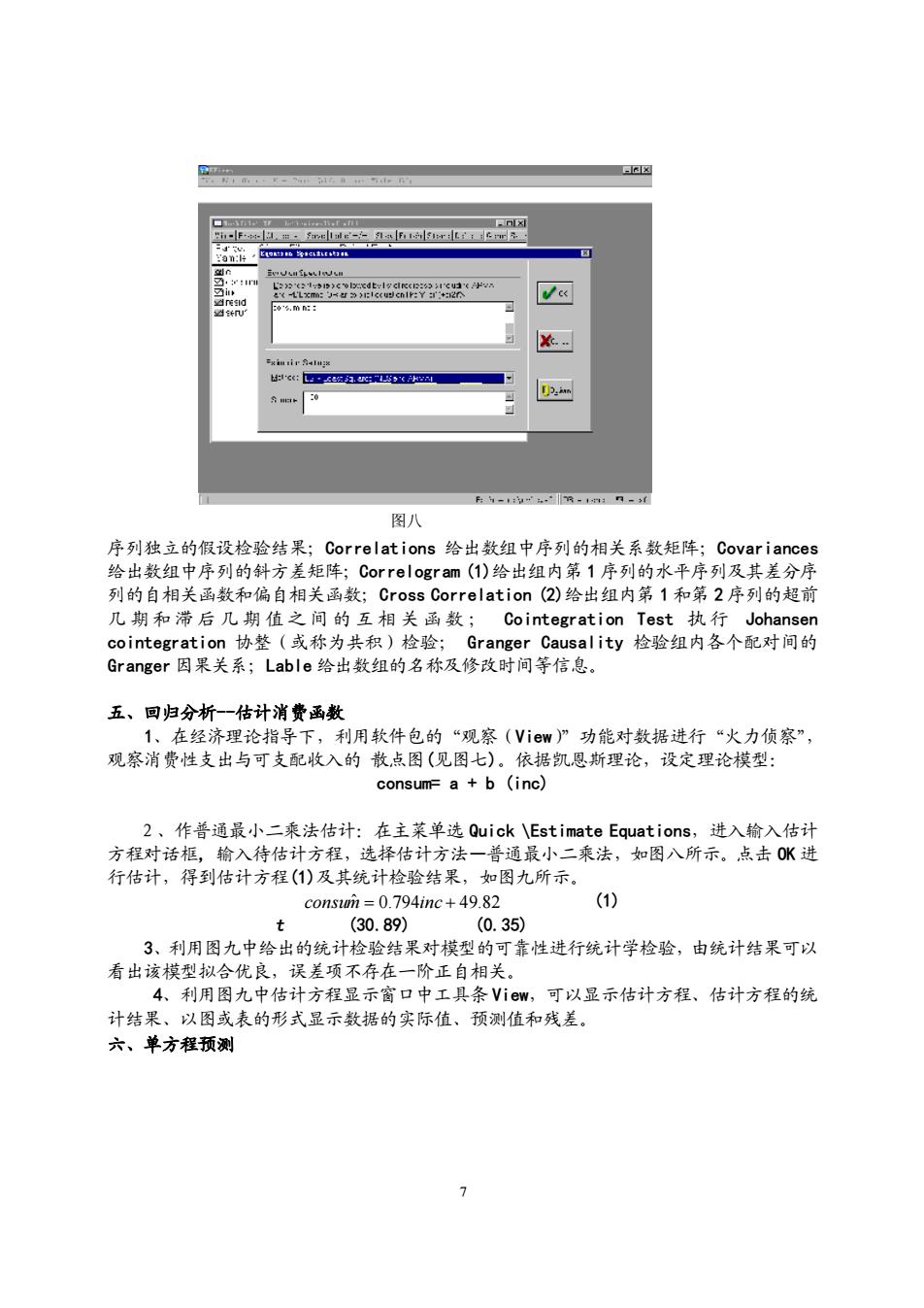
7 序列独立的假设检验结果;Correlations 给出数组中序列的相关系数矩阵;Covariances 给出数组中序列的斜方差矩阵;Correlogram (1)给出组内第 1 序列的水平序列及其差分序 列的自相关函数和偏自相关函数;Cross Correlation (2)给出组内第 1 和第 2 序列的超前 几 期 和 滞 后 几 期 值 之 间 的 互 相 关 函 数 ; Cointegration Test 执 行 Johansen cointegration 协整(或称为共积)检验; Granger Causality 检验组内各个配对间的 Granger 因果关系;Lable 给出数组的名称及修改时间等信息。 五、回归分析-估计消费函数 1、在经济理论指导下,利用软件包的“观察(View)”功能对数据进行“火力侦察”, 观察消费性支出与可支配收入的 散点图(见图七)。依据凯恩斯理论,设定理论模型: consum= a + b (inc) 2、作普通最小二乘法估计:在主菜单选 Quick \Estimate Equations,进入输入估计 方程对话框, 输入待估计方程,选择估计方法—普通最小二乘法,如图八所示。点击 OK 进 行估计,得到估计方程(1)及其统计检验结果,如图九所示。 consumˆ = 0.794inc + 49.82 (1) t (30.89) (0.35) 3、利用图九中给出的统计检验结果对模型的可靠性进行统计学检验,由统计结果可以 看出该模型拟合优良,误差项不存在一阶正自相关。 4、利用图九中估计方程显示窗口中工具条 View,可以显示估计方程、估计方程的统 计结果、以图或表的形式显示数据的实际值、预测值和残差。 六、单方程预测 图八

预测是我们建立经济计量模型的目的之一,其操作如下:进入方程估计输出窗口(可以选 定一个已有的方程建打开或估计一个新方程)如图九,点击其工具栏中的Forecast打开对 n uda5) ,。n:m表n3:n 8 9n解 图九 话柜(图十输入序列名(Forecast name) 这名称通常与方程中被解释变量的名字不 同, ,这样就不会混淆实际值和预测值;作为可选项,可给预测标准差随意命名 [S.E(optional)],命名后,指定的序列将存储于工作文件中;用户可以根据需要选择预测 区间(sample range for forecast )Dynamic选项是利用滞后左手变量以前的预测只来 计算当前样本区间的预测值,Static选项是利用滞后左手变量的实际值来计算预测值(该 洗项只有在实际数值可以得到时使用),当方程中不今有带后被解径变量或AMA项时,这 西种方法在篇一步和以后冬步都给出相同结果当方程中今有带后被解径李或AA项 这两种方法在第二步 ,可洗轻用因形粉估刷估 或两者都用以 评价指标(平均绝对误差等)。将对话柜的内客输入完毕 点击OK得 到用户命名的预测值序列。 注意:在进行外推预测之前应给解释变量赋值。例如我们根据19801998年数据得到 中国人均生活费支出与人均可支配收入关系的回归方程,希望预测1999、2000、2001年的 人均生活费支出。为此,我们首先需要给出1999、2000、2001年人均收入可支配的数据, 如果1999、2000、2001我们从历史数据中得不到1999、2000、2001年人均收入可支配的 数据,就应利用其他方法估计出这些数据,把1999、2000、2001年人均收入可支配的数据 (可能是估计值)输入解释变量中就可以预测出这三年的人均生活费支出
8 预测是我们建立经济计量模型的目的之一, 其操作如下:进入方程估计输出窗口(可以选 定一个已有的方程建打开或估计一个新方程)如图九,点击其工具栏中的 Forecast 打开对 话框(图十),输入序列名(Forecast name), 这名称通常与方程中被解释变量的名字不 同, 这样就不会混淆实际值和预测值;作为可选项,可给预测标准差随意命名 [S.E(optional)],命名后,指定的序列将存储于工作文件中;用户可以根据需要选择预测 区间(sample range for forecast);Dynamic 选项是利用滞后左手变量以前的预测只来 计算当前样本区间的预测值,Static 选项是利用滞后左手变量的实际值来计算预测值(该 选项只有在实际数值可以得到时使用),当方程中不含有滞后被解释变量或 ARMA 项时,这 两种方法在第二步和以后各步都给出相同结果,当方程中含有滞后被解释变量或 ARMA 项 时,这两种方法在第二步以后给出不同结果;用 Output 可选择用图形或数值来看预测值, 或两者都用以及预测评价指标(平均绝对误差等)。将对话框的内容输入完毕,点击 OK 得 到用户命名的预测值序列。 注意:在进行外推预测之前应给解释变量赋值。例如我们根据 1980~1998 年数据得到 中国人均生活费支出与人均可支配收入关系的回归方程,希望预测 1999、2000、2001 年的 人均生活费支出。为此,我们首先需要给出 1999、2000、2001 年人均收入可支配的数据, 如果 1999、2000、2001 我们从历史数据中得不到 1999、2000、2001 年人均收入可支配的 数据,就应利用其他方法估计出这些数据,把 1999、2000、2001 年人均收入可支配的数据 (可能是估计值)输入解释变量中就可以预测出这三年的人均生活费支出。 图九

Vx 图十 实验资料:我国城市居民家庭消费函数一 一元线性回归模型 一、研究的目的要求 居民消货在社会经济的持续发展中有着重要的作用。居民合理的消费模式和居民适度 的消贵规模有利于经济持续健康的增长,而且这也是人民生活水平的具体体现。改革开放 以来随着中国经济的快速发展,人民生活水平不断提高,居民的消费水平也不断增长。但 是在看到这个整体趋势的同时,还应看到全国各地区经济发展速度不同,居民消费水平也 有明显差异。例如,2002年全国城市居民家庭平均每人每年消费支出为6029.88元,最低 的黑龙江省仅为人均4462.08元,最高的上海市达人均10464元,上海是黑龙江的2.35倍。 为了研究全国居民消费水平及其变动的原因,需要作具体的分析。影响各地区居民消费支 出有明显差异的因素可能很多,例如,居民的收入水平、就业状况、零售物价指数、利率 居民财产、购物环境等等都可能对居民消费有影响。为了分析什么是影响各地区居民消贵 支出有明显差异的最主要因素,并分析影响因素与消费水平的数量关系,可以建立相应的 计量经济模型去研究, 二、模型设定 我们研究的对象是各地区居民消费的差异。居民消费可分为城市居民消费和农村居民
9 实验资料: 我国城市居民家庭消费函数——一元线性回归模型 一、研究的目的要求 居民消费在社会经济的持续发展中有着重要的作用。居民合理的消费模式和居民适度 的消费规模有利于经济持续健康的增长,而且这也是人民生活水平的具体体现。改革开放 以来随着中国经济的快速发展,人民生活水平不断提高,居民的消费水平也不断增长。但 是在看到这个整体趋势的同时,还应看到全国各地区经济发展速度不同,居民消费水平也 有明显差异。例如,2002 年全国城市居民家庭平均每人每年消费支出为 6029.88 元, 最低 的黑龙江省仅为人均 4462.08 元,最高的上海市达人均 10464 元,上海是黑龙江的 2.35 倍。 为了研究全国居民消费水平及其变动的原因,需要作具体的分析。影响各地区居民消费支 出有明显差异的因素可能很多,例如,居民的收入水平、就业状况、零售物价指数、利率、 居民财产、购物环境等等都可能对居民消费有影响。为了分析什么是影响各地区居民消费 支出有明显差异的最主要因素,并分析影响因素与消费水平的数量关系,可以建立相应的 计量经济模型去研究。 二、模型设定 我们研究的对象是各地区居民消费的差异。居民消费可分为城市居民消费和农村居民 图十