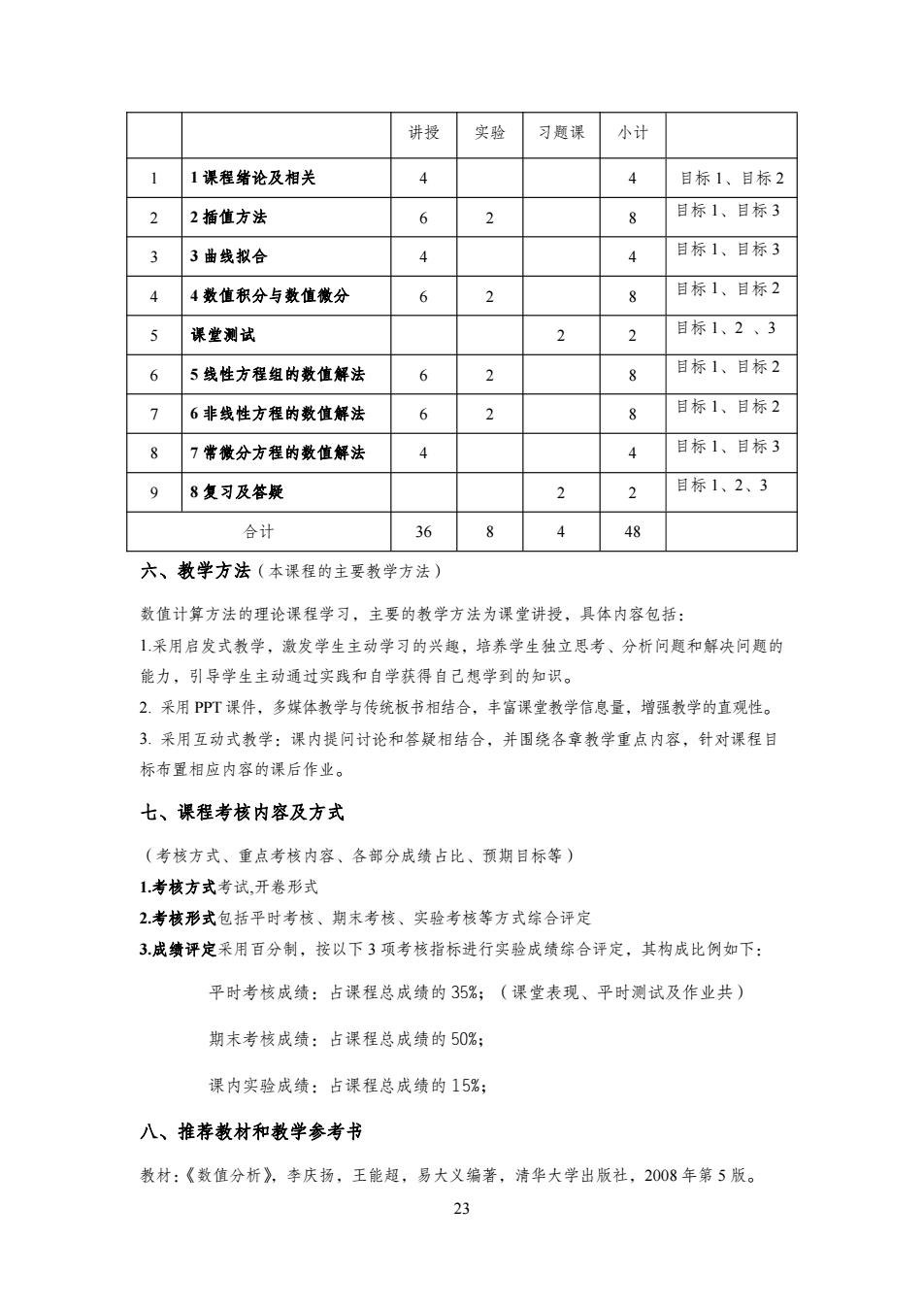
讲授 实验 习题课 小计 1课程绪论及相关 4 4 目标1、目标2 2 2插值方法 6 8 目标1、目标3 3 3曲线拟合 4 4 目标1、目标3 4数值积分与数值微分 6 2 8 目标1、目标2 5 课堂测试 2 2 目标1、2、3 6 5线性方程组的数值解法 6 2 8 目标1、目标2 7 6非线性方程的数值解法 6 2 8 目标1、目标2 8 7常微分方程的数值解法 4 目标1、目标3 9 8复习及答疑 2 2 目标1、2、3 合计 36 8 4 48 六、教学方法(本课程的主要教学方法)》 数值计算方法的理论课程学习,主要的教学方法为课堂讲授,具体内容包括: 1采用启发式教学,激发学生主动学习的兴趣,培养学生独立思考、分析问题和解决问题的 能力,引导学生主动通过实践和自学获得自己想学到的知识。 2.采用PPT课件,多媒体教学与传统板书相结合,丰富课堂教学信息量,增强教学的直观性。 3.采用互动式教学:课内提问讨论和答疑相结合,并围绕各章教学重点内容,针对课程目 标布置相应内容的课后作业。 七、课程考核内容及方式 (考核方式、重点考核内容、各部分成绩占比、预期目标等) 1考核方式考试,开卷形式 2考核形式包括平时考核、期末考核、实验考核等方式综合评定 3成绩评定采用百分制,按以下3项考核指标进行实验成绩综合评定,其构成比例如下: 平时考核成绩:占课程总成绩的35%;(课堂表现、平时测试及作业共) 期末考核成绩:占课程总成绩的50%; 课内实验成绩:占课程总成绩的15%; 八、推荐教材和教学参考书 教材:《数值分析》,李庆扬,王能超,易大义编著,清华大学出版社,2008年第5版。 23
23 讲授 实验 习题课 小计 1 1 课程绪论及相关 4 4 目标 1、目标 2 2 2 插值方法 6 2 8 目标 1、目标 3 3 3 曲线拟合 4 4 目标 1、目标 3 4 4 数值积分与数值微分 6 2 8 目标 1、目标 2 5 课堂测试 2 2 目标 1、2 、3 6 5 线性方程组的数值解法 6 2 8 目标 1、目标 2 7 6 非线性方程的数值解法 6 2 8 目标 1、目标 2 8 7 常微分方程的数值解法 4 4 目标 1、目标 3 9 8 复习及答疑 2 2 目标 1、2、3 合计 36 8 4 48 六、教学方法(本课程的主要教学方法) 数值计算方法的理论课程学习,主要的教学方法为课堂讲授,具体内容包括: 1.采用启发式教学,激发学生主动学习的兴趣,培养学生独立思考、分析问题和解决问题的 能力,引导学生主动通过实践和自学获得自己想学到的知识。 2. 采用 PPT 课件,多媒体教学与传统板书相结合,丰富课堂教学信息量,增强教学的直观性。 3. 采用互动式教学:课内提问讨论和答疑相结合,并围绕各章教学重点内容,针对课程目 标布置相应内容的课后作业。 七、课程考核内容及方式 (考核方式、重点考核内容、各部分成绩占比、预期目标等) 1.考核方式考试,开卷形式 2.考核形式包括平时考核、期末考核、实验考核等方式综合评定 3.成绩评定采用百分制,按以下 3 项考核指标进行实验成绩综合评定,其构成比例如下: 平时考核成绩:占课程总成绩的 35%;(课堂表现、平时测试及作业共) 期末考核成绩:占课程总成绩的 50%; 课内实验成绩:占课程总成绩的 15%; 八、推荐教材和教学参考书 教材:《数值分析》,李庆扬,王能超,易大义编著,清华大学出版社,2008 年第 5 版

参考书:《数值计算方法》,马东升,董宁编著,机械工业出版社,2015年第3版。 参考书:《数值计算方法》,吕同富,康兆敏,方秀男编著,清华大学出版社,2013年第2版。 参考书:《数值方法(MATALAB版)》,(美)Mathews,.JH.等著,周璐等译,电子工业出版社, 2005年第4版。 参考书:《Matlab数值计算》,Cleve B.Moler著,张志涌等编译,北京航空航天大学出版社, 2015年第1版。 撰写人:汪海鹰 审核人: 学院分管领导签字(盖章): 2018年6月6日 24
24 参考书:《数值计算方法》,马东升,董宁编著,机械工业出版社,2015 年第 3 版。 参考书:《数值计算方法》,吕同富,康兆敏,方秀男编著,清华大学出版社,2013 年第 2 版。 参考书:《数值方法(MATALAB 版)》,(美)Mathews,J.H.等著,周璐等译,电子工业出版社, 2005 年第 4 版。 参考书:《Matlab 数值计算》,Cleve B.Moler 著,张志涌等编译,北京航空航天大学出版社, 2015 年第 1 版。 撰写人: 汪海鹰 审核人: 学院分管领导签字(盖章): 2018 年 6 月 6 日

《运筹与优化》课程教学大纲 一、课程概况 课程代码:04451280 课程名称:运筹与优化 课程学分:3.5 课程学时:56(理论学时:56;实验(实践)学时:0) 课程性质:专业教育课程(必修)】 开课部门:信息科学与工程学院 建议修读学期:3 建议先修课程:高等代数、数学分析、概率统计、数学软件及应用 适用专业(方向):信息与计算科学 二、课程地位、作用与任务 《运筹与优化》是信息与计算科学专业的专业基础课程,是数学与应用数学、信息与计 算科学专业的一门重要的专业核心课,也是学位课程。 本课程兼有逻辑的数学和数学的逻辑的性质,是系统工程学和现代管理科学中的一种基 础理论和不可缺少的方法、手段和工具。通过本课程的学习,使学生获得数学建模和经济管 理决策中常用的运筹学的基本概念、基本理论与基本方法的知识;培养学生分析问题和解决 问题的能力;支撑专业毕业要求中相应指标点的达成。 三、课程目标 (一)教学目标 运筹与优化课程具体要求达到的特定教学目标包括: 1教学目标1.掌握运筹学的基本概念、基本理论和基本方法,包括线性规划及单纯型法、 线性规划的对偶理论、运输问题、整数规划与分配问题、图与网络分析、排队论、决策分析 等;了解运筹学的基本应用:能根据实际问题建立相应的运筹学模型,并掌握求解问题的计 算方法,为数学建模莫定坚实基础。培养与提升学生对实际问题运用定量方法分析与求解, 以及进行辅助决策的能力。培养学生综合运用所学知识去分析解决问题的素质,培养最优化 方法的数学素养。(指标点4.1) (二)本课程支撑的半业要求 1.本课程支撑的毕业要求:(毕业要求4。)(毕业要求见2018版人才培养方案) 2.本课程支撑的指标点:指标点4.1 (1)指标点41:熟悉建模基础知识,具备较强的数学建模分析能力。 (三)课程教学目标与毕业要求对应表 《运筹与优化》课程教学目标与毕业要求的对应表 25
25 《运筹与优化》课程教学大纲 一、课程概况 课程代码:04451280 课程名称:运筹与优化 课程学分:3.5 课程学时:56(理论学时:56;实验(实践)学时:0) 课程性质:专业教育课程(必修) 开课部门:信息科学与工程学院 建议修读学期:3 建议先修课程:高等代数、数学分析、概率统计、数学软件及应用 适用专业(方向):信息与计算科学 二、课程地位、作用与任务 《运筹与优化》是信息与计算科学专业的专业基础课程,是数学与应用数学、信息与计 算科学专业的一门重要的专业核心课,也是学位课程。 本课程兼有逻辑的数学和数学的逻辑的性质,是系统工程学和现代管理科学中的一种基 础理论和不可缺少的方法、手段和工具。通过本课程的学习,使学生获得数学建模和经济管 理决策中常用的运筹学的基本概念、基本理论与基本方法的知识;培养学生分析问题和解决 问题的能力;支撑专业毕业要求中相应指标点的达成。 三、课程目标 (一)教学目标 运筹与优化课程具体要求达到的特定教学目标包括: 1.教学目标 1. 掌握运筹学的基本概念、基本理论和基本方法,包括线性规划及单纯型法、 线性规划的对偶理论、运输问题、整数规划与分配问题、图与网络分析、排队论、决策分析 等;了解运筹学的基本应用;能根据实际问题建立相应的运筹学模型,并掌握求解问题的计 算方法,为数学建模奠定坚实基础。培养与提升学生对实际问题运用定量方法分析与求解, 以及进行辅助决策的能力。培养学生综合运用所学知识去分析解决问题的素质,培养最优化 方法的数学素养。(指标点 4.1) (二)本课程支撑的毕业要求 1. 本课程支撑的毕业要求:(毕业要求 4。)(毕业要求见 2018 版人才培养方案) 2. 本课程支撑的指标点:指标点 4.1 (1)指标点 4.1:熟悉建模基础知识,具备较强的数学建模分析能力。 (三)课程教学目标与毕业要求对应表 《运筹与优化》课程教学目标与毕业要求的对应表

课程名称:运筹与优化 任课教师:刘春燕 课程性质:专业必修 课程学分:3.5 课程支撑的毕业要求 课程目标、达成途径、评价依据 毕业要求4: 教学目标:培养与提升学生对实际问题运用定量方法分 4.1熟悉建模基础知识,具备较强 析与求解,以及进行辅助决策的能力。培养学生综合运 的数学建模分析能力。 用所学知识去分析解决问题的素质,培养最优化方法的 数学素养。 达成途径:通过课程学习运筹学的基本概念、基本理论 和基本方法,包括线性规划及单纯型法、线性规划的对 偶理论、运输问题、整数规划与分配问题、图与网络分 析、排队论和决策分析等;了解运筹学的基本应用;能 根据实际问题建立相应的运筹学模型,并掌握求解问题 的计算方法,为数学建模奠定坚实基础。 评价依据:课堂提问和练习、课外作业、期中测验和期 末考试。 四、课程内容 教学内容 作业要求 第一章线性规划及单纯形法 自学内容: 1.1一般线性规划问题的数学模型 绪论:运筹学的产生与发展;运筹学在 1.2图解法 管理中的应用状况:运筹学模型的分类以及 1.3单纯形法原理 模型的有关概念。 1.4单纯形的计算步骤 1.6数据包络分析 1.5单纯形法的进一步讨论 课堂作业: 1.7应用举例 知识点: 案例分析与讨论 课外作业: 1.一般线性规划问题的数学模型,线性规划的 概念及其数学模型 1完成本章小结 2.线性规划的图解法 2.完成本章习题 3.单纯形法求解原理 4.单纯形法的迭代计算步骤及单纯形法的矩 阵形式 5.单纯形法的进一步讨论及线性规划问题的 分解 6线性规划方法解决经济、管理中的线性的最 优化问题。 第二章线性规划的对偶理论 自学内容: 2.1对偶问题的提出 2.5对偶单纯形法 2.2原问题与对偶问题 2.7参数线性规划 2.3对偶问题的基本性质 课堂作业: 2.4影子价格 2.5灵敏度分析 案例分析与讨论 课外作业: 26
26 课程名称:运筹与优化 任课教师:刘春燕 课程性质:专业必修 课程学分:3.5 课程支撑的毕业要求 课程目标、达成途径、评价依据 毕业要求 4: 4.1 熟悉建模基础知识,具备较强 的数学建模分析能力。 教学目标:培养与提升学生对实际问题运用定量方法分 析与求解,以及进行辅助决策的能力。培养学生综合运 用所学知识去分析解决问题的素质,培养最优化方法的 数学素养。 达成途径:通过课程学习运筹学的基本概念、基本理论 和基本方法,包括线性规划及单纯型法、线性规划的对 偶理论、运输问题、整数规划与分配问题、图与网络分 析、排队论和决策分析等;了解运筹学的基本应用;能 根据实际问题建立相应的运筹学模型,并掌握求解问题 的计算方法,为数学建模奠定坚实基础。 评价依据:课堂提问和练习、课外作业、期中测验和期 末考试。 四、课程内容 教学内容 作业要求 第一章 线性规划及单纯形法 1.1 一般线性规划问题的数学模型 1.2 图解法 1.3 单纯形法原理 1.4 单纯形的计算步骤 1.5 单纯形法的进一步讨论 1.7 应用举例 知识点: 1.一般线性规划问题的数学模型,线性规划的 概念及其数学模型 2.线性规划的图解法 3.单纯形法求解原理 4.单纯形法的迭代计算步骤及单纯形法的矩 阵形式 5.单纯形法的进一步讨论及线性规划问题的 分解 6.线性规划方法解决经济、管理中的线性的最 优化问题。 自学内容: 绪论:运筹学的产生与发展;运筹学在 管理中的应用状况;运筹学模型的分类以及 模型的有关概念。 1.6 数据包络分析 课堂作业: 案例分析与讨论 课外作业: 1.完成本章小结 2.完成本章习题 第二章 线性规划的对偶理论 2.1 对偶问题的提出 2.2 原问题与对偶问题 2.3 对偶问题的基本性质 2.4 影子价格 2.5 灵敏度分析 自学内容: 2.5 对偶单纯形法 2.7 参数线性规划 课堂作业: 案例分析与讨论 课外作业:
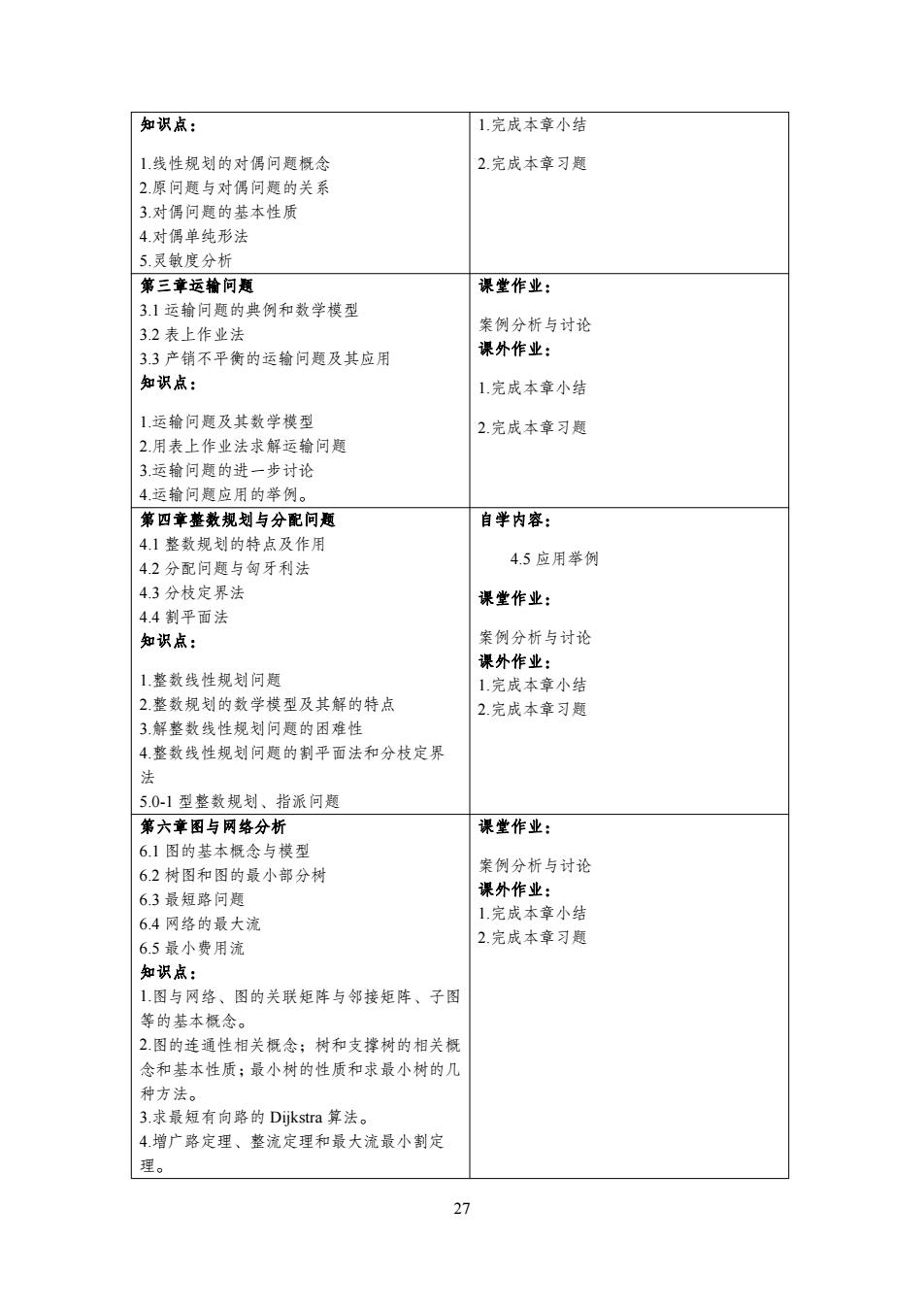
知识点: 1完成本章小结 1线性规划的对偶问题概念 2.完成本章习题 2.原问题与对偶问题的关系 3.对偶问意的基本性质 4.对偶单纯形法 5.灵敏度分析 第三章运输问题 课堂作业: 3.1运输问题的典例和数学模型 3.2表上作业法 案例分析与讨论 3.3产销不平衡的运输问题及其应用 课外作业: 知识点: 1.完成本章小结 1.运输问题及其数学模型 2.完成本章习题 2.用表上作业法求解运输问题 3.运输问题的进一步讨论 4.运输问题应用的举例。 第四章整数规划与分配问题 自学内容: 4.1整数规划的特点及作用 4.2分配问题与匈牙利法 4.5应用举例 4.3分枝定界法 课堂作业: 4.4割平面法 知识点: 案例分析与讨论 课外作业: 1整数线性规划问题 1完成本章小结 2.整数规划的数学模型及其解的特点 2.完成本章习题 3解整数线性规划问题的困难性 4.整数线性规划问题的割平面法和分枝定界 法 5.0-】型整数规划、指派问题 第六章图与网络分析 课堂作业: 6.1图的基本概念与模型 6.2树图和图的最小部分树 案例分析与讨论 6.3最短路问题 课外作业: 6.4网络的最大流 1完成本章小结 6.5最小费用流 2.完成本章习题 知识点: 1图与网络、图的关联矩阵与邻接矩阵、子图 等的基本概念。 2.图的连通性相关概念;树和支撑树的相关概 念和基本性质;最小树的性质和求最小树的几 种方法。 3.求最短有向路的Dijkstra算法。 4.增广路定理、整流定理和最大流最小割定 理。 27
27 知识点: 1.线性规划的对偶问题概念 2.原问题与对偶问题的关系 3.对偶问题的基本性质 4.对偶单纯形法 5.灵敏度分析 1.完成本章小结 2.完成本章习题 第三章运输问题 3.1 运输问题的典例和数学模型 3.2 表上作业法 3.3 产销不平衡的运输问题及其应用 知识点: 1.运输问题及其数学模型 2.用表上作业法求解运输问题 3.运输问题的进一步讨论 4.运输问题应用的举例。 课堂作业: 案例分析与讨论 课外作业: 1.完成本章小结 2.完成本章习题 第四章整数规划与分配问题 4.1 整数规划的特点及作用 4.2 分配问题与匈牙利法 4.3 分枝定界法 4.4 割平面法 知识点: 1.整数线性规划问题 2.整数规划的数学模型及其解的特点 3.解整数线性规划问题的困难性 4.整数线性规划问题的割平面法和分枝定界 法 5.0-1 型整数规划、指派问题 自学内容: 4.5 应用举例 课堂作业: 案例分析与讨论 课外作业: 1.完成本章小结 2.完成本章习题 第六章图与网络分析 6.1 图的基本概念与模型 6.2 树图和图的最小部分树 6.3 最短路问题 6.4 网络的最大流 6.5 最小费用流 知识点: 1.图与网络、图的关联矩阵与邻接矩阵、子图 等的基本概念。 2.图的连通性相关概念;树和支撑树的相关概 念和基本性质;最小树的性质和求最小树的几 种方法。 3.求最短有向路的 Dijkstra 算法。 4.增广路定理、整流定理和最大流最小割定 理。 课堂作业: 案例分析与讨论 课外作业: 1.完成本章小结 2.完成本章习题