
麦克斯韦方程组的复数形式 Re)Rel(Re Re[VxH(r)e]=Re{[J(r)+j@D(r)lei) Re{[VxH(r)-J(r)-j@D(r)]e/)=0 对于任意时刻t上式都成立 VxH(r)=J(r)+joD(r) 复数形式的全电流定理 lexu@mail.xidian.edu.cn 12
麦克斯韦方程组的复数形式 lexu@mail.xidian.edu.cn 12 Re[ ( ) ] Re[ ( ) ] Re{ [ ( ) ]} j t j t j t Hre Jre Dre t ωω ω ∂ ∇× = + ∂ Re[ ( ) ] Re{[ ( ) ( )] } j t j t Hre Jr j Dr e ω ω ∇× = + ω Re{[ ( ) ( ) ( )] } 0 j t Hr Jr j Dr e ω ∇× − − ω = 对于任意时刻t上式都成立 ∇× = + Hr Jr j Dr () () () ω 复数形式的全电流定理 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

麦克斯韦方程组的复数形式 ·复数形式的麦克斯韦方程组 VxH(r)=J(r)+j@D(r) V×Er))=土joBr) V.B(r)=0 V.D(r)=p ●复数形式的电流连续性方程 lexu@mail.xidian.edu.cn VxJ--jop
麦克斯韦方程组的复数形式 复数形式的麦克斯韦方程组 复数形式的电流连续性方程 lexu@mail.xidian.edu.cn 13 ∇× = + Hr Jr j Dr () () () ω ∇× = − Er j Br () () ω ∇⋅ = B r() 0 ∇⋅ = D r( ) ρ ∇× = − J jωρ XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN

麦克斯韦方程组的复数形式 。瞬时值表示的麦克斯韦方程组可以用复数形式来描述: 。场量和场源的瞬时值换成对应复数形式; 对于微分方程,将时间求导运算换成0: 麦克斯韦方程组由四变量函数转换成三变量函数; 。麦克斯韦方程组的微分形式由偏微分方程转换成了代数 方程; ●为书写方便,复振幅上的小点以后略去不标。 lexu@mail.xidian.edu.cn 14
麦克斯韦方程组的复数形式 瞬时值表示的麦克斯韦方程组可以用复数形式来描述: 场量和场源的瞬时值换成对应复数形式; 对于微分方程,将时间求导运算换成jω; 麦克斯韦方程组由四变量函数转换成三变量函数; 麦克斯韦方程组的微分形式由偏微分方程转换成了代数 方程; 为书写方便,复振幅上的小点以后略去不标。 lexu@mail.xidian.edu.cn 14 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN
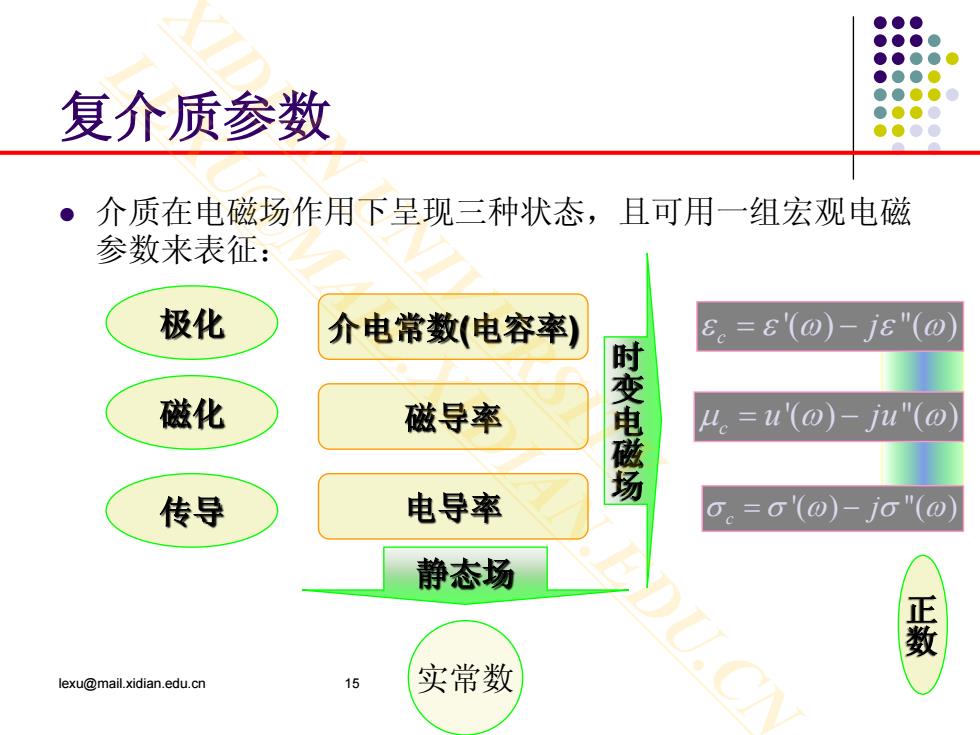
复介质参数 ● 介质在电磁场作用下呈现三种状态,且可用一组宏观电磁 参数来表征: 极化 介电常数(电容率) 6。=8'(0)-j8"(0 磁化 磁导率 变电磁场 =u'(0)-ju"(0 传导 电导率 0。=0'(0)-j0"(0 静态场 轰 lexu@mail.xidian.edu.cn 15 实常数
复介质参数 介质在电磁场作用下呈现三种状态,且可用一组宏观电磁 参数来表征: lexu@mail.xidian.edu.cn 15 极化 磁化 传导 介电常数(电容率) 磁导率 电导率 实常数 静态场 时变电磁场 '( ) "( ) c ε εω ε ω = − j '( ) "( ) c σ σω σ ω = − j '( ) "( ) c µω ω = − u ju 正数 XIDIAN UNIVERSITY LEXU@MAIL.XIDIAN.EDU.CN