
【例1]用旋转矢量法讨论质点初始时 刻位移为以下情况时谐振动的初相 位:0A;0-A;口0,且向负方向 运动;口-AV2,且向正方向运动 解:0p=0 元 三 2 4死 或0= 2 3 3
[例1]用旋转矢量法讨论质点初始时 刻位移为以下情况时谐振动的初相 位: A; -A; 0,且向负方向 运动; -A/2,且向正方向运动 O x 2 A − − A A 解: = 0 = 2 = 3 4 3 4 = 3 2 或 = − 2

三相位差和相位的超前与落后 设x1=A4C0s(0t+9 x2=A,C0$(02t+p2) 相位差△p=(0,t+42)-(0t+9 =(02-0)t+(92-9〉 同频率时△0=P2一P -初相差与t无关
三.相位差和相位的超前与落后 cos( ) 1 = 1 1 +1 x A t cos( ) 2 = 2 2 +2 x A t 设 相位差 ( ) ( ) = 2 +2 − 1 +1 t t ( ) ( ) = 2 −1 + 2 −1 t 同频率时 =2 −1 -初相差与t 无关

讨论: 0△p=0即?2=9-同相 0△p=±π即p=9,±π-反相 0△0>0即p2>9 一第二个谐振动超前 第一个谐振动△0
讨论: = 0 即 2 =1 -同相 = 即 2 =1 -反相 0 即 2 1 -第二个谐振动超前 第一个谐振动
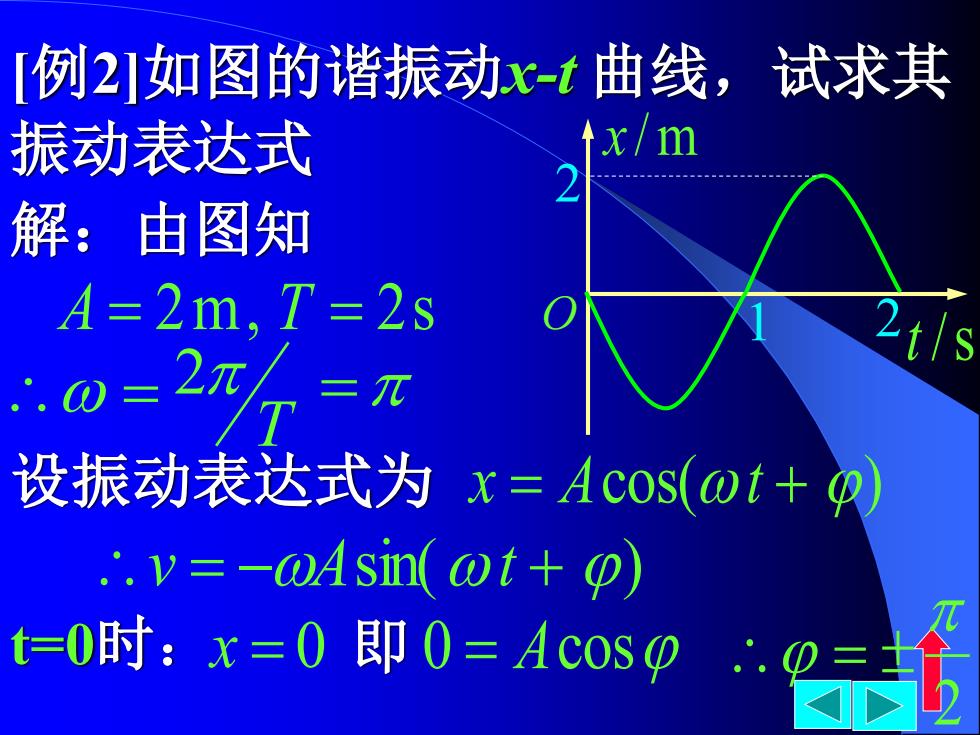
[例2如图的谐振动x-t曲线,试求其 振动表达式 个x/m 解:由图知 A=2m,T=2s 0=2 T =π 设振动表达式为x=ACos(ωt+p .v=-OAsin(@t+p) t=0时:x=0即0=Ac0s 0.2
[例2]如图的谐振动x-t 曲线,试求其 振动表达式 t /s x /m O 2 1 2 解:由图知 A = 2m, T = 2s T = 2 = 设振动表达式为 x = Acos(t + ) v = −Asin(t + ) t=0时: x = 0 0 = Acos 2 即 =

又v<0即-oAsin p<0 ∴.sinp>0→9= 2 X=2以a+ 旋转矢量法 2
又 v 0 即 −Asin 0 sin 0 2 = ) m 2 2cos( x = t + O x 2 旋转矢量法 2 =