
第9章模拟信号的数字传输 。【例9.1】设一个均匀量化器的量化电平数为M,其输入信号 抽样值在区间[-α,a内具有均匀的概率密度。试求该量化器 的平均信号量噪比。 【解】 N,-2om-9fm,-立m-g,2a -立+a-+品 ) M(4v) 24a 因为 MAv =2a 所以有 N= (△v)2 12 21
21 第9章模拟信号的数字传输 【例9.1】设一个均匀量化器的量化电平数为M,其输入信号 抽样值在区间[-a, a]内具有均匀的概率密度。试求该量化器 的平均信号量噪比。 【解】 因为 所以有 ( ) a v M v a dm a v m a i v dm a N m q f m dm m q M i M i a i v a i v k k M i m m k i k M i m m q k i k k i i i i 2 12 24 1 2 1 ) 2 ( 2 1 ( ) ( ) ( ) 3 1 2 1 ( 1) 2 1 2 1 2 1 1 = = = + − + = − = − = = − + − + − = = − − Mv = 2a ( ) 12 2 v Nq =

第9章模拟信号的数字传输 由于此信号具有均匀的概率密度,故信号功率等于 S,=L.mi 2a 12(4月 所以,平均信号量噪比为 Na 或写成 201g M dB q dB 由上式可以看出,量化器的平均输出信号量噪比随量化电平 数M的增大而提高。 22
22 第9章模拟信号的数字传输 由于此信号具有均匀的概率密度,故信号功率等于 所以,平均信号量噪比为 或写成 由上式可以看出,量化器的平均输出信号量噪比随量化电平 数M的增大而提高。 − = = a a q k k v M dm a S m 2 2 2 ( ) 2 12 1 2 M N S q q = M N S dB q q = 20lg dB

第9章模拟信号的数字传输 9.4.3非均匀量化 ◆非均匀量化的目的:在实际应用中,对于给定的量化 器,量化电平数M和量化间隔都是确定的,量化噪 声N也是确定的。但是,信号的强度可能随时间变化 (例如,语音信号)。当信号小时,信号量噪比也小。 所以,这种均匀量化器对于小输入信号很不利。为了 克服这个缺点,改善小信号时的信号量噪比,在实际 应用中常采用非均匀量化。 23
23 第9章模拟信号的数字传输 ◼ 9.4.3 非均匀量化 ◆ 非均匀量化的目的:在实际应用中,对于给定的量化 器,量化电平数M和量化间隔v都是确定的,量化噪 声Nq也是确定的。但是,信号的强度可能随时间变化 (例如,语音信号)。当信号小时,信号量噪比也小。 所以,这种均匀量化器对于小输入信号很不利。为了 克服这个缺点,改善小信号时的信号量噪比,在实际 应用中常采用非均匀量化
第章模拟信号的数字传输 ◆非均匀量化原理 ▣在非均匀量化时,量化间隔随信号抽样值的不同而变化。 信号抽样值小时,量化间隔也小;信号抽样值大时,量 化间隔4也变大。 实际中,非均匀量化的实现方法通常是在进行量化之前, 先将信号抽样值压缩,再进行均匀量化。如右图所示: 图中纵坐标y是均匀刻 度的,横坐标x是非均 匀刻度的。所以输入电 压越小,量化间隔也就 越小。也就是说,小信号 的量化误差也小。 24
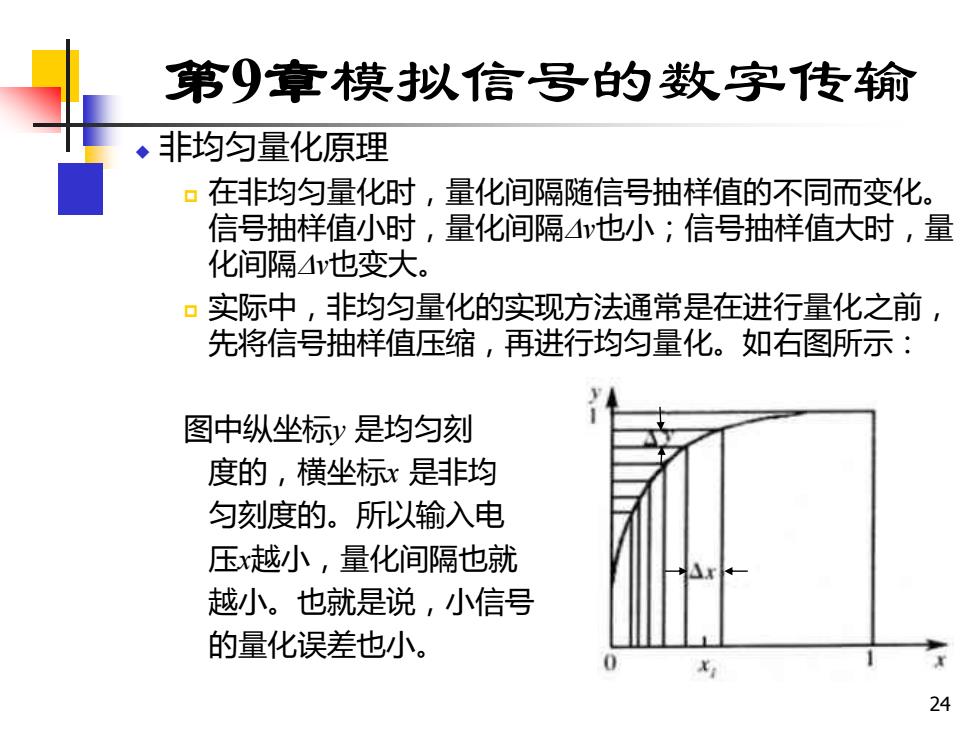
24 第9章模拟信号的数字传输 ◆ 非均匀量化原理 在非均匀量化时,量化间隔随信号抽样值的不同而变化。 信号抽样值小时,量化间隔v也小;信号抽样值大时,量 化间隔v也变大。 实际中,非均匀量化的实现方法通常是在进行量化之前, 先将信号抽样值压缩,再进行均匀量化。如右图所示: 图中纵坐标y 是均匀刻 度的,横坐标x 是非均 匀刻度的。所以输入电 压x越小,量化间隔也就 越小。也就是说,小信号 的量化误差也小

第9章模拟信号的数字传输 ◆非均匀量化的数学分析 当量化区间划分很多时,在每一量化区间内压缩特性曲 线可以近似看作为一段直线。因此,这段直线的斜率可 以写为: △y- 2-y △xdx 并有 dx △x= △y dy 设此压缩器的输入和输出电压范围都限制在0和1之间,y 轴每个量化区间的间隔等于 1 △y= 得到 dx 1 dx △X= d △y= NAx dy N dy dy 25
25 第9章模拟信号的数字传输 ◆ 非均匀量化的数学分析 当量化区间划分很多时,在每一量化区间内压缩特性曲 线可以近似看作为一段直线。因此,这段直线的斜率可 以写为: 并有 设此压缩器的输入和输出电压范围都限制在0和1之间,y 轴每个量化区间的间隔等于 得到 y dx dy x y = = y dy dx x = N y 1 = dy dx N y dy dx x 1 = = N x dy dx =