
第章模拟信号的数字传输 9.4抽样信号的量化 9.4.1量化原理 ◆设模拟信号的抽样值为m(kT),此抽样值仍然是一个 取值连续的变量。若仅用个不同的二进制数字码 元来代表此抽样值的大小,则W个不同的二进制码 元只能代表M=2个不同的抽样值。因此,必须将 抽样值的范围划分成M个区间,每个区间用一个电 平表示。这样,共有M个离散电平,它们称为量化 电平。用这M个量化电平表示连续抽样值的方法称 为量化。 16
16 第9章模拟信号的数字传输 ⚫ 9.4 抽样信号的量化 ◼ 9.4.1 量化原理 ◆ 设模拟信号的抽样值为m(kT),此抽样值仍然是一个 取值连续的变量。若仅用N个不同的二进制数字码 元来代表此抽样值的大小,则N个不同的二进制码 元只能代表M = 2N个不同的抽样值。因此,必须将 抽样值的范围划分成M个区间,每个区间用一个电 平表示。这样,共有M个离散电平,它们称为量化 电平。用这M个量化电平表示连续抽样值的方法称 为量化
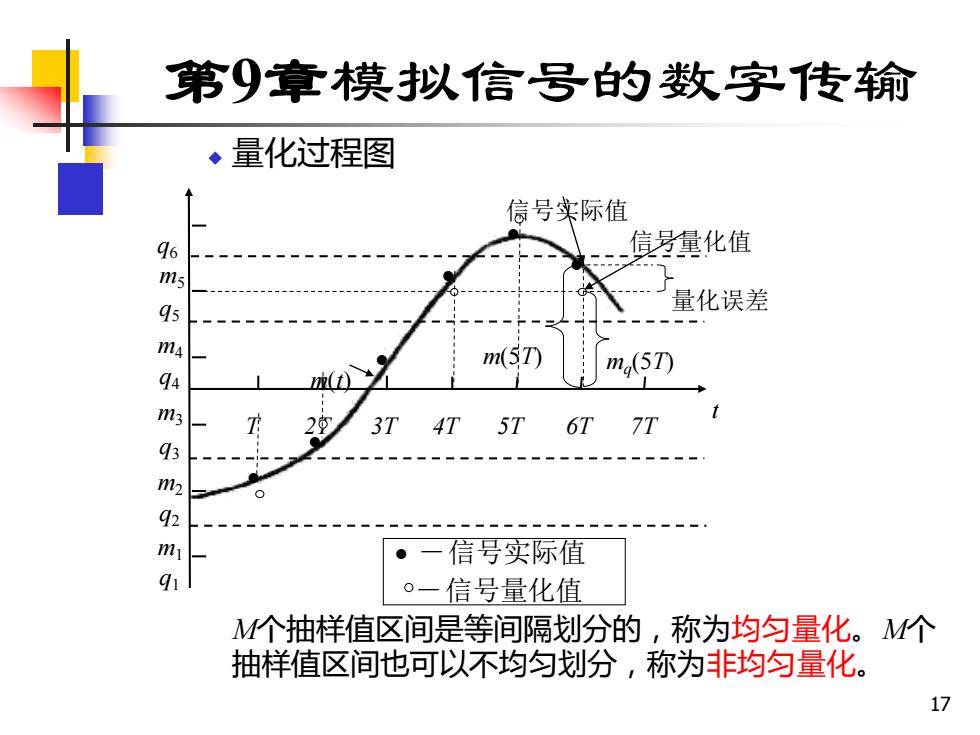
第9章模拟信号的数字传输 ◆量化过程图 信号实际值 96 信另量化值 量化误差 m(5T) ma(5T) 37 41 5T 67 7T ·一信号实际值 ·一信号量化值 M个抽样值区间是等间隔划分的,称为均匀量化。M个 抽样值区间也可以不均匀划分,称为非均匀量化。 17
17 第9章模拟信号的数字传输 ◆ 量化过程图 M个抽样值区间是等间隔划分的,称为均匀量化。M个 抽样值区间也可以不均匀划分,称为非均匀量化。 m1 m2 m4 m3 m5 q5 q4 q3 q2 q1 T 2T 3T 4T 5T 6T 7T t 量化误差 信号实际值 信号量化值 m(t) • • • • • • m(5T) mq (5T) q6 • - 信号实际值 - 信号量化值
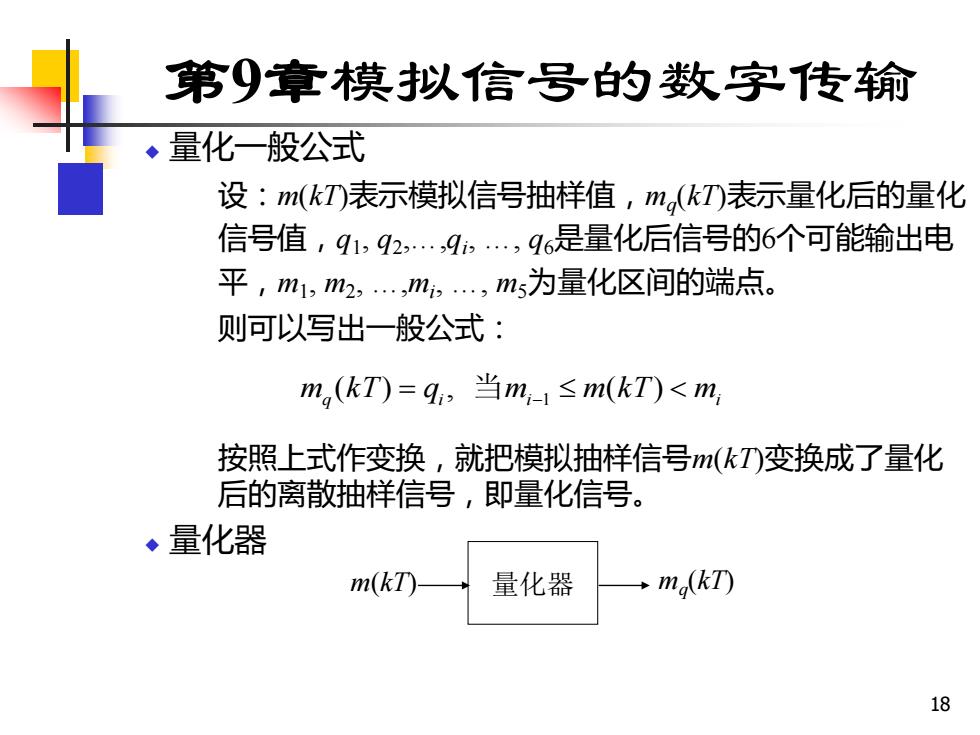
第章模拟信号的数字传输 ◆量化一般公式 设:m(kT表示模拟信号抽样值,m,(kT)表示量化后的量化 信号值,91,92,.,9,.,96是量化后信号的6个可能输出电 平,m1,m2,.,m,.,m5为量化区间的端点。 则可以写出一般公式: m(kT)=q,当m-1≤m(kT)<m 按照上式作变换,就把模拟抽样信号m(kTD变换成了量化 后的离散抽样信号,即量化信号。 ◆量化器 m(kT) 量化器 ma(kT) 18
18 第9章模拟信号的数字传输 ◆ 量化一般公式 设:m(kT)表示模拟信号抽样值,mq (kT)表示量化后的量化 信号值,q1 , q2 ,.,qi , ., q6是量化后信号的6个可能输出电 平,m1 , m2 , .,mi , ., m5为量化区间的端点。 则可以写出一般公式: 按照上式作变换,就把模拟抽样信号m(kT)变换成了量化 后的离散抽样信号,即量化信号。 ◆ 量化器 q i i mi m (k T) = q , 当m −1 m(k T) m(kT) 量化器 mq (kT)

第9章模拟信号的数字传输 9.4.2均匀量化 ◆均匀量化的表示式 设模拟抽样信号的取值范围在α和b之间,量化电平数为 M,则在均匀量化时的量化间隔为 b-a △v= M 且量化区间的端点为 m,=a+i△v i=0,1,M 若量化输出电平q取为量化间隔的中点,则 g,="m+m⊥=a+iv-△ 2 分1=12,M 19
19 第9章模拟信号的数字传输 ◼ 9.4.2 均匀量化 ◆ 均匀量化的表示式 设模拟抽样信号的取值范围在a和b之间,量化电平数为 M,则在均匀量化时的量化间隔为 且量化区间的端点为 若量化输出电平qi取为量化间隔的中点,则 M b a v − = m a i v i = + i = 0, 1, ., M i M v a i v m m q i i i , 1,2,., 2 2 1 = = + − + = −

第9章模拟信号的数字传输 ◆量化误差 量化后的信号m)与原信号m)的差m()-mg(们称为量化 误差。这种近似程度常用信号与量化噪声功率比来衡量,即 S Elm2 (KT)] N Elm(kT)-m (kT)] ◆均匀量化的平均信号量噪比 V,=m,-m,P]门-ms-m,f(m )dma&=∑(m:-q,fm,)dmg ◆信号m的平均功率可以表示为 S,=E(m2)=∫m2fme)dm 20
20 第9章模拟信号的数字传输 ◆ 量化误差 量化后的信号mq (t)与原信号m(t)的差[m(t)-mq (t)]称为量化 误差。这种近似程度常用信号与量化噪声功率比来衡量,即 ◆ 均匀量化的平均信号量噪比 ◆ 信号mk 的平均功率可以表示为 = − = − = − = − b a M i m m q k q k q k k k i k k i i N E m m m m f m dm m q f m dm 1 2 2 2 1 [( ) ] ( ) ( ) ( ) ( ) 2 2 [ ( ) ( )] [ ( )] E m kT m kT E m kT N S q q q q − = = = b a q k k mk dmk S E(m ) m f ( ) 2 2