第12章正交编码与伪随机序列 ◆前8个沃尔什函数的波形示于下图中 wal(0,8)+1 0 wal(1.0)o wal(2.) wa3,8) wal) 0 wal(5.0 wal6,8)0 wal(7.8)0 16
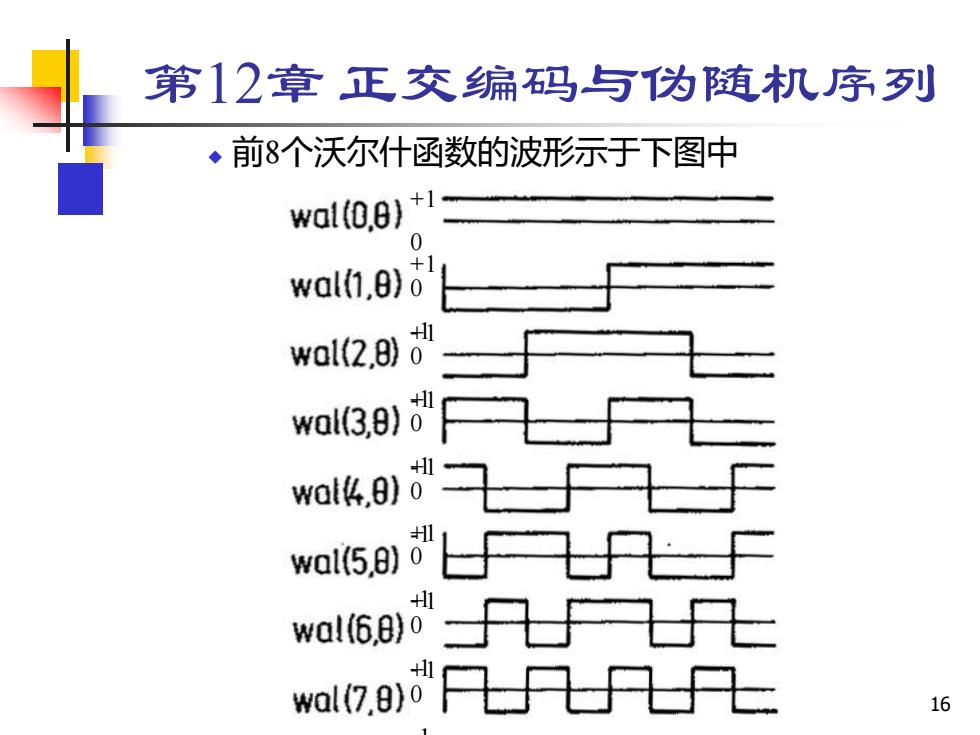
16 第12章 正交编码与伪随机序列 ◆ 前8个沃尔什函数的波形示于下图中 +1 0 +1 0 -+11 0 -+11 0 -+11 0 -+11 0 -+11 0 -+11 0 -1

第12章正交编码与伪随机序列 由于沃尔什函数的取值仅为“+1和”-1”,所以可以用其离 散的抽样值表示成矩阵形式。例如,上图中的8个沃尔什函数 可以写成如下沃尔什矩阵: W= X 由上图和矩阵可以看出,沃尔什矩阵是按照每一行中”+1” 和”-1的交变次数由少到多排列的。 沃尔什函数(矩阵)天生具有数字信号的特性,所以它们在 数字信号处理和编码理论中有不小应用前景。 17
17 第12章 正交编码与伪随机序列 ◆ 由于沃尔什函数的取值仅为“+1”和“-1”,所以可以用其离 散的抽样值表示成矩阵形式。例如,上图中的8个沃尔什函数 可以写成如下沃尔什矩阵: 由上图和矩阵可以看出,沃尔什矩阵是按照每一行中“+1” 和“-1”的交变次数由少到多排列的。 沃尔什函数(矩阵)天生具有数字信号的特性,所以它们在 数字信号处理和编码理论中有不小应用前景。 + − + − + − + − − + − + + − + − − + + − + − − + + − − + + − − + + + − − + + − − − − + + + + − − − − − − + + + + + + + + + + + + W =

第12章正交编码与伪随机序列 12.3伪随机序列 。12.3.1基本概念 ◆什么是伪随机噪声? 具有类似于随机噪声的某些统计特性,同时又能够重复 产生的波形。 ◆优点:它具有随机噪声的优点,又避免了随机噪声的缺 点,因此获得了日益广泛的实际应用。 ◆如何产生伪随机噪声? 目前广泛应用的伪随机噪声都是由周期性数字序列经过 滤波等处理后得出的。在后面我们将这种周期性数字序 列称为伪随机序列。它有时又称为伪随机信号和伪随机 ▣12.3.2m序列 ◆m序列的产生:m序列是最长线性反馈移位寄存器序列的简称。 它是由带线性反馈的移存器产生的周期最长的一种序列。 8
18 第12章 正交编码与伪随机序列 ⚫ 12.3 伪随机序列 ◼ 12.3.1 基本概念 ◆ 什么是伪随机噪声? 具有类似于随机噪声的某些统计特性,同时又能够重复 产生的波形。 ◆ 优点:它具有随机噪声的优点,又避免了随机噪声的缺 点,因此获得了日益广泛的实际应用。 ◆ 如何产生伪随机噪声? 目前广泛应用的伪随机噪声都是由周期性数字序列经过 滤波等处理后得出的。在后面我们将这种周期性数字序 列称为伪随机序列。它有时又称为伪随机信号和伪随机 码。 ◼ 12.3.2 m序列 ◆ m序列的产生:m序列是最长线性反馈移位寄存器序列的简称。 它是由带线性反馈的移存器产生的周期最长的一种序列

第12章正交编码与伪随机序列 。例:下图中示出一个4级线性反馈移存器。 设其初始状态为(a3,a2, a1,a)=(1,0,0,0),则 在移位1次时,由a3和 ao模2相加产生新的输入 初始状态 a4=1⊕0=1,新的状 0 0 0 0 态变为(a4,a3,a2,a1)=( 1 0 1 1 1,1,0,0)。这样移位15 0 1 1 1 次后又回到初始状态(1, 1 1 1 0 1 0 1 0,0,0)0 0 1 0 24-1=15个) 若初始状态为全“0”,目 1 0 1 0 1 2 0 (0,0,0,0),则移位后得 0 0 1 0 到的仍为全“0状态。 0 1 0 1 0 0 该避免出现全“0状态, 0 0 0 0 0 0 1 否则移存器的状态将不 会改变。 1 0 0 0 19
19 第12章 正交编码与伪随机序列 例: 下图中示出一个4级线性反馈移存器。 设其初始状态为(a3 , a2 , a1 , a0 ) = (1, 0, 0, 0),则 在移位1次时,由a3和 a0模2相加产生新的输入 a4 = 1 0 = 1,新的状 态变为(a4 , a3 , a2 , a1 ) = ( 1, 1, 0, 0)。这样移位15 次后又回到初始状态(1, 0, 0, 0)。 若初始状态为全“0”,即 (0, 0, 0, 0),则移位后得 到的仍为全“0”状态。应 该避免出现全“0”状态, 否则移存器的状态将不 会改变

第12章正交编码与伪随机序列 因为4级移存器共有24=16种可能的状态。除全“0”状态外 只剩15种状态可用。这就是说,由任何4级反馈移存器产生 的序列的周期最长为15。 我们常常希望用尽可能少的级数产生尽可能长的序列。由上 例可见,一般来说,一个级线性反馈移存器可能产生的最 长周期等于(2”-1)。我们将这种最长的序列称为最长线性反 馈移存器序列,简称m序列。 反馈电路如何连接才能使移存器产生的序列最长,这就是本 节将要讨论的主题。 20
20 第12章 正交编码与伪随机序列 因为4级移存器共有2 4 = 16种可能的状态。除全“0”状态外, 只剩15种状态可用。这就是说,由任何4级反馈移存器产生 的序列的周期最长为15。 我们常常希望用尽可能少的级数产生尽可能长的序列。由上 例可见,一般来说,一个n级线性反馈移存器可能产生的最 长周期等于(2n - 1)。我们将这种最长的序列称为最长线性反 馈移存器序列,简称m序列。 反馈电路如何连接才能使移存器产生的序列最长,这就是本 节将要讨论的主题