
第12章正交编码与伪随机序列 12.2.2阿达玛矩阵 ◆定义: 口阿达玛矩阵简记为矩阵。它是一种方阵,仅由元素+1 和-1构成,而且其各行(和列)是互相正交的。最低 阶的H矩阵是2阶的,即 +1+1 H2= +1-1 下面为了简单,把上式中的+1和-1简写为+和-,这 样上式变成 11
11 第12章 正交编码与伪随机序列 ◼ 12.2.2 阿达玛矩阵 ◆ 定义: 阿达玛矩阵简记为H矩阵。它是一种方阵,仅由元素+1 和-1构成,而且其各行(和列)是互相正交的。最低 阶的H矩阵是2阶的,即 下面为了简单,把上式中的+1和-1简写为+和-,这 样上式变成 + − + + = 1 1 1 1 H2 + − + + H2 =

第12章正交编码与伪随机序列 阶数为2的幂的高阶H矩阵可以从下列递推关系得出 HN=HN/2图H2 式中,N=2m; ⑧·直积。 上式中直积是指将矩阵H12中的每一个元素用矩阵H,代替。 例如: H2 H: H4=H,®H,=H2-A: + 12
12 第12章 正交编码与伪随机序列 阶数为2的幂的高阶H矩阵可以从下列递推关系得出 H N= H N / 2 H 2 式中,N = 2 m; - 直积。 上式中直积是指将矩阵HN / 2中的每一个元素用矩阵H2代替。 例如: + − − + + + − − + − + − + + + + = − = = 2 2 2 2 2 H H H H H4 H2 H
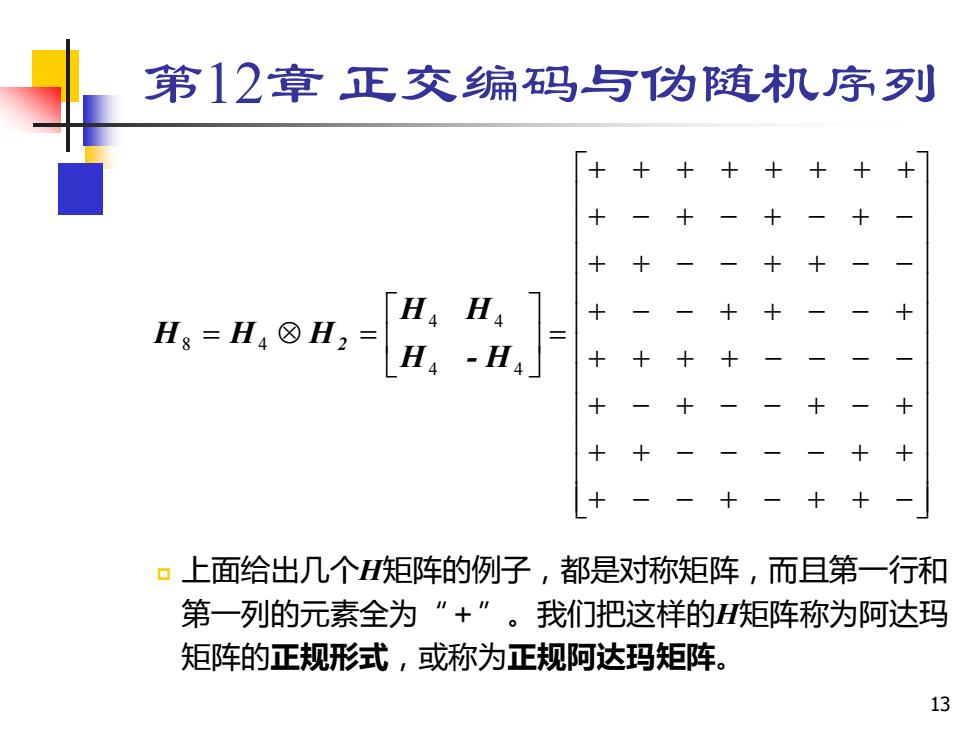
第12章正交编码与伪随机序列 「H4H4 Hg=H4⑧H2= H4-H4 十 + ▣上面给出几个H矩阵的例子,都是对称矩阵,而且第一行和 第一列的元素全为”+”。我们把这样的H矩阵称为阿达玛 矩阵的正规形式,或称为正规阿达玛矩阵。 13
13 第12章 正交编码与伪随机序列 上面给出几个H矩阵的例子,都是对称矩阵,而且第一行和 第一列的元素全为“+”。我们把这样的H矩阵称为阿达玛 矩阵的正规形式,或称为正规阿达玛矩阵。 + − − + − + + − + + − − − − + + + − + − − + − + + + + + − − − − + − − + + − − + + + − − + + − − + − + − + − + − + + + + + + + + = = = 4 4 4 4 8 4 H - H H H H H H2

第12章正交编码与伪随机序列 ◆性质 ▣在H矩阵中,交换任意两行,或交换任意两列,或改变任 一行中每个元素的符号,或改变任一列中每个元素的符号 都不会影响矩阵的正交性质。因此,正规H矩阵经过上述 各种交换或改变后仍为矩阵,但不一定是正规的了。 ▣按照递推关系式可以构造出所有2阶的矩阵。可以证明 高于2阶的H矩阵的阶数一定是4的倍数。不过,以4的倍数 作为阶数是否一定存在矩阵,这一问题并未解决。 ▣矩阵是正交方阵。若把其中每一行看作是一个码组,则 这些码组也是互相正交的,而整个H矩阵就是一种长为的 正交编码,它包含n个码组。因为长度为n的编码共有2n个 不同码组,现在若只将这n个码组作为准用码组,其余(2” )个为禁用码组,则可以将其多余度用来纠错。这种编码 在纠错编码理论中称为里德缪勒(Reed-Muller)码。 14
14 第12章 正交编码与伪随机序列 ◆ 性质 在H矩阵中,交换任意两行,或交换任意两列,或改变任 一行中每个元素的符号,或改变任一列中每个元素的符号, 都不会影响矩阵的正交性质。因此,正规H矩阵经过上述 各种交换或改变后仍为H矩阵,但不一定是正规的了。 按照递推关系式可以构造出所有2 k阶的H矩阵。可以证明, 高于2阶的H矩阵的阶数一定是4的倍数。不过,以4的倍数 作为阶数是否一定存在H矩阵,这一问题并未解决。 H矩阵是正交方阵。若把其中每一行看作是一个码组,则 这些码组也是互相正交的,而整个H矩阵就是一种长为n的 正交编码,它包含n个码组。因为长度为n的编码共有2 n个 不同码组,现在若只将这n个码组作为准用码组,其余(2n - n)个为禁用码组,则可以将其多余度用来纠错。这种编码 在纠错编码理论中称为里德-缪勒(Reed-Muller)码

第12章正交编码与伪随机序列 12.2.3沃尔什函数和沃尔什矩阵 ◆沃尔什函数定义 wal2j+p,0)=(-1)/2p{wal(Uj,2(0+1/4】+(-1)+walj,2(0-1/4]} wal0,-={0 -1/2≤0<1/2 0<-1/2,0≥1/2 式中p=0或1,j=0,1,2,.,及指数中的/2]表示取j/2 的整数部分。 ◆正弦和余弦函数可以构成一个完备正交函数系。由于正 弦和余弦函数具有完备和正交性,所以由其构成的无穷 级数或积分(即傅里叶级数和傅里叶积分)可以表示任 一波形。类似地,由取值”+1和”-1构成的沃尔什 函数也具有完备正交性,也可以用其表示任一波形 15
15 第12章 正交编码与伪随机序列 ◼ 12.2.3 沃尔什函数和沃尔什矩阵 ◆ 沃尔什函数定义 式中 p = 0或1,j = 0,1,2,,及指数中的[j / 2]表示取j / 2 的整数部分。 ◆ 正弦和余弦函数可以构成一个完备正交函数系。由于正 弦和余弦函数具有完备和正交性,所以由其构成的无穷 级数或积分(即傅里叶级数和傅里叶积分)可以表示任 一波形。类似地,由取值“+1”和“-1”构成的沃尔什 函数也具有完备正交性,也可以用其表示任一波形 (2 , ) ( 1) [( ,2( 1/ 4)] ( 1) [ ,2( 1/ 4)] / 2 + = − + + − − + + wal j p wal j wal j j p j p − − = 0 1/ 2, 1/ 2 1 1/ 2 1/ 2 (0, ) wal