
1.齐次坐标 4、通过二点的直线 4 如果 X1= 为三图象点,则通过 该二点的直线的参数向量为:L=X1×x2 x=0 Ix2=0 X2
4、通过二点的直线 如果 为二图象点,则通过 该二点的直线的参数向量为: 1 2 1 1 2 2 1 2 , u u x v x v t t = = 1 2 L = x x L x1 = 0 L x2 = 0 T T L x1 x2 1. 齐次坐标

1.齐次坐标 5、平行线可以相交 笛卡尔坐标系下,两条直线的方程为: Ax+By+C=0 Ax+By+D=0 齐次坐标系下,两条直线的方程为: A不+B上+C=0 w w Ax+By+Cw=0 A+B上+D=0 Ax+By+Dw=0 w w 可以解出w=0,即两条直线相交于无穷远点
5、平行线可以相交 1. 齐次坐标 笛卡尔坐标系下,两条直线的方程为: 齐次坐标系下,两条直线的方程为: 可以解出w=0,即两条直线相交于无穷远点
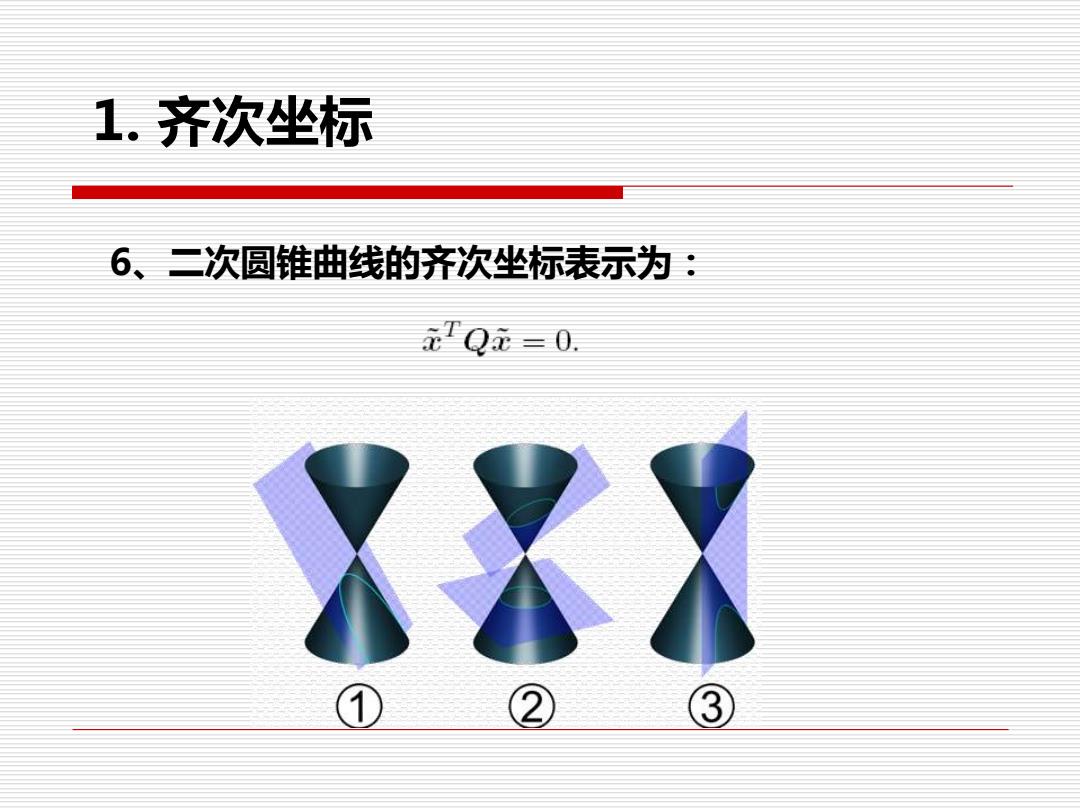
1.齐次坐标 6、二次圆锥曲线的齐次坐标表示为: 元Q元=0 ① 2 3
6、二次圆锥曲线的齐次坐标表示为: 1. 齐次坐标
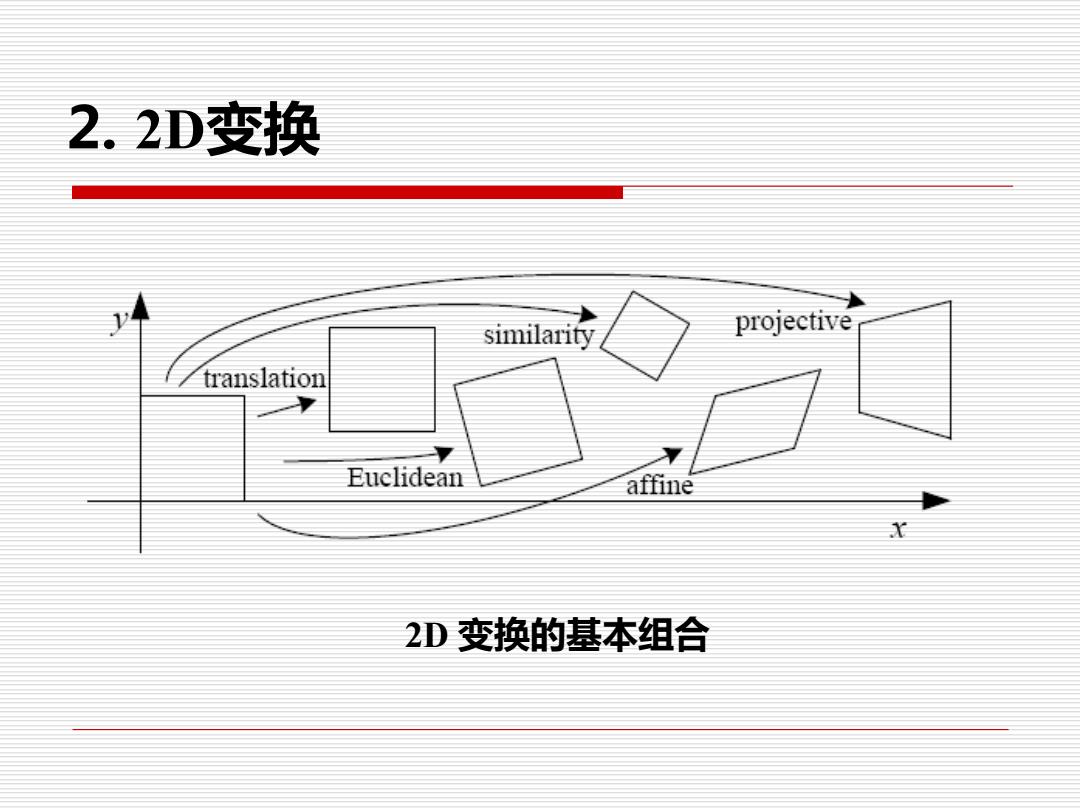
2.2D变换 similarity projective translation Euclidean affine 2D变换的基本组合
2. 2D变换 2D 变换的基本组合

2D变换 2D平移变预可猫述为: ] 或者: 2D旋转、平移变换可描述为: R t R= cos0 sin sin A cos 0
2D变换 2D平移变换可描述为: 或者: 2D旋转、平移变换可描述为: