电子科技大学：《先进控制技术 Advanced Control Technology》课程教学资源（课件讲稿）02 最优控制

3.用变分法求解最优控制问题 3.用变分法求解最优控制问题 3.用变分法求解最优控制问题 例4投系统状志方程为立一“ -0.502-g1+6,-0 垃界条作0-1,0)-0 ,一器 -4-05644-0 这确定鼓优控制)使与+2油为极小 -7%-32g+4e,+6,-15←x29+52白-15 小4，- 解这是与白由择端国定的最优解问题 -36-0.5g%-e4c.+￥-5 ,小-u,-1→，-E Hn34a -26-1506e9g,+5折-2 a-2-5。--5 解得6-0.7乃 0.3 兽a4 --c,)+c:--i+1 m'()--ce'+c1=0.13e'+0.73 物制方程-0++及-0→d -号 +的 皮用边界条骨 w'--E 0-+马-1 小号 3.用变分法求解最优控制问题 3.用变分法求解最优控制问题 3.用变分法求解最优控制问题 例5授拉制对象方程为主一址 3()-cre'cse- 择端时刻1，自由，将鸡型定，)-一 i(1)=cue'-cze-w 于是量优轨线和最优控制左 求")和▣'()使得J-广任，恤为假水 由边舞条特和横截条件0)=马 2--2m 解本题，自由，路溶国定 ,尝 当。<4'u)-,e“'()-"u-x,e2 H-2++w=x2+w2+2m u,+2u,+2,,》-0 器 x2u)=m0,)=e, 当>4x')-ew')-')--e” [,)+,,)-,月-0 .明→-2 99-0 由，》一G可求地降端时魏 0-048a i-t 9,*4- 64-0 li-m→应-i+i-i-0 收4=x6G=0成9=09= 11

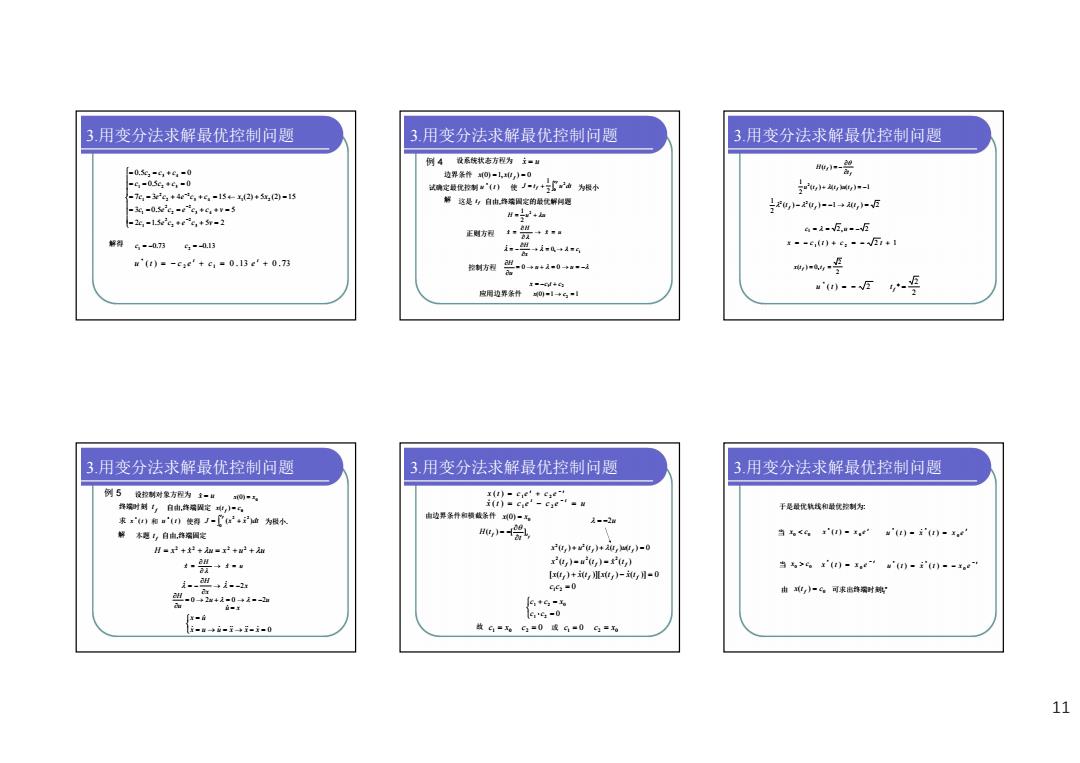
11                                        2 1.5 5 2 3 0.5 5 7 3 4 15 (2) 5 (2) 15 0.5 0 0.5 0 3 2 2 2 1 3 4 2 2 2 1 3 4 1 2 2 2 2 1 1 2 3 2 3 4 c e c e c v c e c e c c v c e c e c c x x c c c c c c 解得 0.73 c1   0.13 c2   ( ) 0 . 13 0 .73 2 1 *      t t u t c e c e 3.用变分法求解最优控制问题 例 4 设系统状态方程为 x  u 边界条件 x(0)  1, x(t f )  0 试确定最优控制 ( ) * u t 使    f t J t f u dt 0 2 2 1 为极小 解 这是 f t 自由,终端固定的最优解问题 H  u  u 2 2 1 正则方程 x u H x         1 0, c x H            控制方程           u u u H 0 0 应用边界条件 (0) 1 1 x   c2  1 2 x  c t  c 3.用变分法求解最优控制问题 f f t H t      ( ) ( ) ( ) ( ) 1 2 1 2 u t f   t f u t f   ( ) ( ) 1 ( ) 2 2 1 2 2  t f   t f     t f  c1    2,u   2 x   c 1 (t )  c 2   2 t  1 2 2 x(t f )  0,t f  ( ) 2 * u t   2 2 t f *  3.用变分法求解最优控制问题 例 5 设控制对象方程为 x  u 0 x(0)  x 终端时刻 f t 自由,终端固定 0 x(t ) c f  求 ( ) * x t 和 ( ) * u t 使得    f t J x x dt 0 2 2 (  ) 为极小. 解 本题 f t 自由,终端固定 H  x  x  u  x  u  u 2 2 2 2  x u H x         x x H   2         u u u H  0  2   0   2     u  x           x u u x x x 0 x u       3.用变分法求解最优控制问题 t t x t c e c e   1  2 ( ) x t c e c e u t t     1 2  ( ) 由边界条件和横截条件 0 x(0)  x f f t t H (t ) [ ]      ( ) ( ) ( ) ( ) 0 2 2 x t f  u t f   t f u t f  ( ) ( ) ( ) 2 2 2 f f f x t  u t  x t [ ( )  ( )][ ( )  ( )]  0 f f f f x t x t x t x t 0 c1c2         0 1 2 1 2 0 c c c c x 故 1 0 c  x 0 c2  或 0 c1  2 0 c  x   2u 3.用变分法求解最优控制问题 于是最优轨线和最优控制为: 当 0 0 x  c t x t x e0 * ( )  t u t x t x e0 * * ( )   ( )  当 0 0 x  c t x t x e   0 * ( ) t u t x t x e     0 * * ( )  ( ) 0 x(t ) c 由 可求出终端时刻 f  t f* 3.用变分法求解最优控制问题

3用变分法求解最优控制问题 3.用变分法求解最优控制问题 3.用变分法求解最优控制问题 例6强场控制的直流电内机如图所示 代入给定边界条骨 最学根型 这是给定，心圆定的最优控刺问题 H-,2+2+4名-，2+码+ 9-0 -6 正则方程 片小 4 4尝46 则最优控制为 - 边界条补 尝n 年 [图 防园二00w- 最优性能霜标了广一广动一卫安 件院器标」-上出 代入状志方程料 n-ju,u-Ter-tc446 数代转线 年要 卖整9修金量具有限本时的信制入 0-j恤--e4e 4牛 4极小值原理及其应用 4.极小值原理及其应用-洁时阿系线极小原四 4.极小值原理及其应用-连时阿系战：即要 用古典变分法解数代拉制倒题时，履定用不受知机从百得到量优控刺端足 设系统状志方程友 。 令-04》-0 )=flx,r(u,小 z'们-505-.明 断上在工型问圆中，控制瘦绿总有一定的网制 初始条朴气)-©，R”,世≤D“”,口为有界闭集不等式约束为 且2f=G0MwM】z-0 设控刺使量藏限制在某一闭集内型©口 可八八1之0，G为m喻连续可微的向单函数，■金P 于是，系统方程灯 生▣自xd, u0满足Gw(,】≥0 系统风儿转体到蜂编状老山。1末给定，锋鸡状志x心满足等式约来 2-0A 满足限刺条件的u将为客许控制，由千心U不能是任意的， M,h4,=0 到6-4=4)-0国=0 型.0的条件己不存在 M知指连坡可微向量南数，9三m 锋病时球末给定锋端的束，从，=0 菱求确定最代拉制山·应使性能指标 性能指标：了-[x,h,】+化F工以，]恤 最优旋制钢恩铁是要寻找最代容许控刺的使)为假小 J-1,k,小+必Flsth oun%小恤 为极小 12

12 例6 磁场控制的直流电动机如图所示 M I const a  Rf Uf Lf 数学模型 f x x u              1 0 0 0 0 1  x k y f         0   边界条件              (0) 0 (0) (0) 0 2 1  x x x        0 0 ( )1 x t 性能指标   1 0 2 t J u f dt 1 t 给定 试求在t1 时间内由x(0)转移到x(t1 ),并使控制能量具有极小值时的控制输入(励磁 电压)uf* ,最优性能指标J*和最优轨线x(t)*, 3.用变分法求解最优控制问题 解: 这是t f 给定,x(tf) 固定的最优控制问题 f f f H u x x u x u 1 2 2 2 1 1 2 2 2             正则方程 1 1 1 1 0 c x H           1 2 1 2 2 2 c t c x H               控制方程  0   u f H 2 1 2 2 1 2 1 2u 0 u c t c f     f   代入状态方程得 2 3 2 2 1 2 1 4 1 x (t) u (t)dt c t c t c  f     3 4 2 2 3 1 2 1 4 1 12 1 x (t)  x (t)dt  c t  c t  c t  c  3.用变分法求解最优控制问题 代入给定边界条件 3 1 0 1 24 t c   2 12 1 0 2 t c   0 c3  4 0 c   则最优控制为 1 2 * 2 1 2 1 u f  c t  c 2 1 0 3 1 * 0 12 6 t t t u f     最优性能指标    1 0 3 1 2 0 * t * 2 12 f t J u dt  最优轨线 t t t t x 2 1 2 0 3 1 0 2 * 6  6    0 2 2 1 3 0 3 1 0 1 * 2 3      t  t t t x 3.用变分法求解最优控制问题 用古典变分法解最优控制问题时,假定u(t)不受限制,从而得到最优控制应满足  0   u H 实际上在工程问题中,控制变量总有一定的限制. 设控制变量被限制在某一闭集内 u  即u(t)满足 G[ x(t), u (t), t]  0 满足限制条件的u(t)称为容许控制，由于δu不能是任意的,  0   u H 的条件已不存在 4.极小值原理及其应用 设系统状态方程为: x(t)  f [ x(t), u(t), t] 初始条件 ( ) (0), , , 0 n p x t  x x  R u  R Ω为有界闭集,不等式约束为 G[ x(t), u(t), t]  0, G为m维连续可微的向量函数, m  p 系统从x0 转移到终端状态x(tf)，t f 未给定,终端状态x(tf)满足等式约束 M[x(t f ),t f ]  0 M为q 维连续可微向量函数, q  n 性能指标:    f t t f f J x t t F x t u t t dt 0  [ ( ), ] [ ( ), ( ), ] 最优控制问题就是要寻找最优容许控制u(t)使J为极小 4.极小值原理及其应用-连续时间系统极小值原理 令 ( ) ( ) ( ) 0  t  u t  t0  [ ( )] [ ( ), ( ), ] ( ) 0 ( ) [ ( ), ( ), ( )] 0 2 1 2    Z t G x t u t t Z t Z t z t z t z t m T   且 于是,系统方程为: ( ) ( ) 0 ( ) 0 ( , , ) ( , , ) 0 0 0 0 2      x t x z t t Z G x t x f x t        终端时刻t f 未给定,终端约束 M[x(t f ),t f ]  0 要求确定最优控制 u  使性能指标    f t t J x t f t f F x t t t dt 0  [ ( ), ] [ ( ),  ( ), ] 为极小 4.极小值原理及其应用-连续时间系统极小值原理