电子科技大学：《先进控制技术 Advanced Control Technology》课程教学资源（课件讲稿）02 最优控制

2数学准备-泛函极值问题 2数学准备-泛函极值问题 2数学准备-泛函极值问题 2:未给定终端时刻的泛函极值问题 -F'th emni(ncitldr 由横维条件可推出各种情况下的边界条件 wn+,k,'50-0 着始时。定，始状态国定或沿规定的边由线修：面时球白 10◆-电，1电，M,5,-0 1》给定始溶和自向许漏 贵整盟电动城定的仿动这关处优签州题你之为瑞定瑞 上式第二项分尾樱生 女时，邓=%-04自由 投系统性能指标J-广F种 可得边舞条件与精酸条什为% 于是有： 式中，是己知的。未给定，x哈定或末给定 +,r,h,'5t-0 -=0 x)▣x')+) 0·4'0+),-,+写) 得取极植得必要条件为 F,h,,门-0 J-4"FIro+go+ruh 我拉方湿 普-出箬=0 由手最优轨找四你御是最优时球，上式可写为： J取酸的要条为 0=0。 横酸条件 +F'h5r-0- 。》=6 -0=0。 无条作约束的泛动极值问中的边界条和横条列表 2数学准备-泛函极值问题 2.数学准备-泛函极值问题 州定 品餐 %=。 xu）-y 2》给定兰4和锋有的电0-C和置。 (3)择编国定，始端有约束。=州。 艘 ,, 装w-0 x(t)-x(0+cnn) 定 边界条件与横截条作为： 代入，)-Cy) 6图 f%-玉4 告…，-0 rg+e+e可+5= x(tt)=x $田 -0装，-0 =耶+tr川=q可+5月 )=a】 上式求编绿。开红=0 g+c4,+c》 告-0Fu小-0 器 ,)=。 {,=0F,小，-0 国宽 w-ai-ivabin 的来 ,l=Cr） e-om告-r儿，。 从以上讨论可以看出。不论边郭情况如南。泛两龄值影必溺满足成拉方程， 可得边界条作与桶截条作为： =0 只是在求解城拉方程时。对干不可边界棉况。应采用不同的边界柔作与精截 的来 到4▣6 条件 电定 偿wen-儿 6

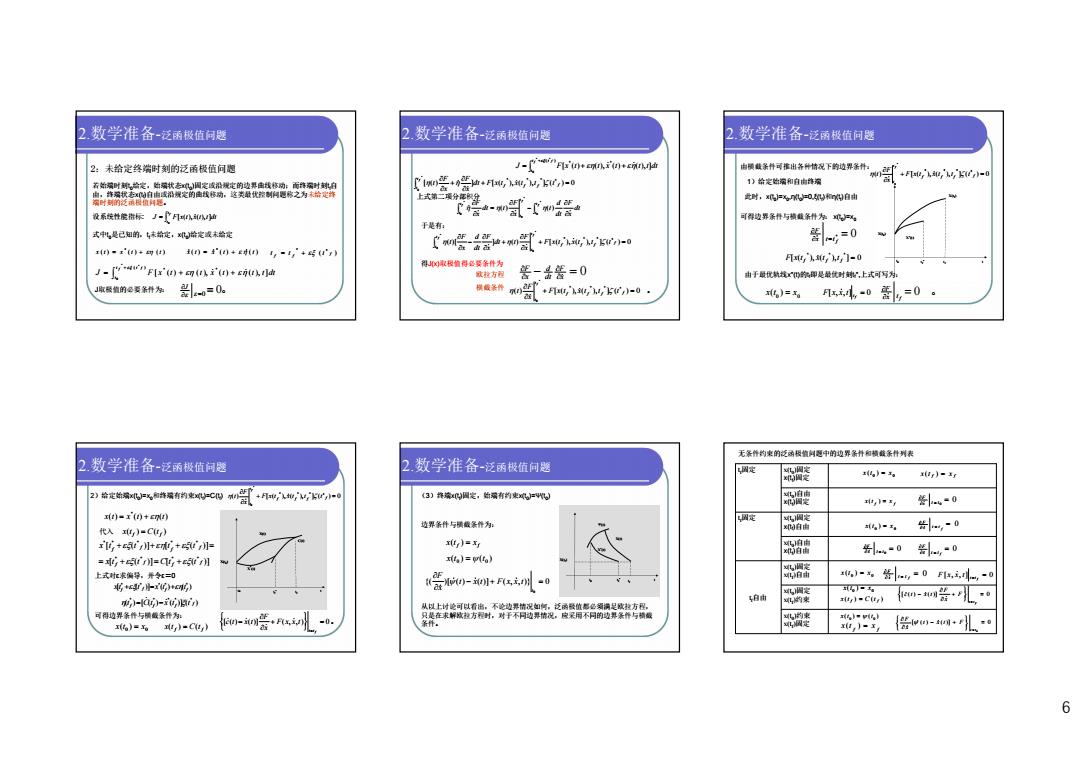
6 2：未给定终端时刻的泛函极值问题 若始端时刻t0 给定，始端状态x(t0 )固定或沿规定的边界曲线移动；而终端时刻t f 自 由，终端状态x(tf)自由或沿规定的曲线移动，这类最优控制问题称之为未给定终 端时刻的泛函极值问题。 设系统性能指标: J F x t x t t dt f t t [ ( ), ( ), ] 0    式中t0 是已知的，t f 未给定，x(t0 )给定或未给定 ( ) ( ) ( ) * x t  x t   t ( ) ( ) ( ) * x t  x t    t ( ) * * f f f t  t   t J F x t t x t t t dt f f t t t [ ( ) ( ), ( ) ( ), ] ( ) * * * * 0          J取极值的必要条件为：    J  0  0。 2.数学准备-泛函极值问题 [ ( ) ] [ ( ), ( ), ] ( ) 0 * * * * * 0         f f f f t t dt F x t x t t t x F x F t f       上式第二项分部积分           * 0 * 0 * 0 ( ) ( ) f f f t t t t t t dt x F dt d t x F dt t x F       于是有： ( )[ ] ( ) [ ( ), ( ), ] ( ) 0 * * * * * 0 * 0            f f f f t t t t F x t x t t t x F dt t x F dt d x F t f f       得J(x)取极值得必要条件为   0     x F dt d x F 欧拉方程  横截条件 ( ) [ ( ), ( ), ] ( * ) 0 。 * * * * 0     f f f f t t F x t x t t t x F t f     J F x t t x t t t dt f f t t t [ ( ) ( ), ( ) ( ), ] ( ) * * * * 0          2.数学准备-泛函极值问题 由横截条件可推出各种情况下的边界条件： 1）给定始端和自由终端 X(t0 ) t0 tf t X* (t) X(tf ) tf* 此时，x(t0 )=x0 ,η(t0 )=0,ξ(tf)和η(tf)自由 可得边界条件与横截条件为： x(t0 )=x0 *  0    f x t t F  [ ( ), ( ), ] 0 * * * F x t f x t f t f  由于最优轨线x*(t)的t f 即是最优时刻t f*,上式可写为： 0 0 x(t )  x [ , , ]  0 f t F x x t   F x t f  0 。 ( ) [ ( ), ( ), ] ( ) 0 * * * * * 0     f f f f t t F x t x t t t x F t f     2.数学准备-泛函极值问题 2）给定始端x(t0 )=x0 和终端有约束x(tf)=C(tf) X(t0 ) t0 tf t X* (t) X(t) tf* C(t) ( ) ( ) ( ) * x t  x t   t 代入 ( ) ( ) f f x t  C t [ ( )] [ ( )] [ ( )] [ ( )] * * * * * * * * * f f f f f f f f x t t C t t x t t t t              上式对ε求偏导，并令ε＝0 ( ) [ ( ) ( )] ( ) * * * * * f f f f  t C t x t  t    可得边界条件与横截条件为： 0 0 x(t )  x ( ) ( ) f f x t  C t [ ( ) ( )] ( , , )  0。            f t t F x x t x F c t x t     ( ) [ ( ), ( ), ] ( ) 0 * * * * * 0     f f f f t t F x t x t t t x F t f     2.数学准备-泛函极值问题 [ ( )] ( ) ( ) * * * * * f f f f x t  t x t t （3）终端x(tf)固定，始端有约束x(t0 )=Ψ(t0 ) X(tf ) t0 tf t X* (t) X(t) tf* 边界条件与横截条件为： Ψ(t) f f x(t )  x ( ) ( ) 0 0 x t  t {( )[ ( ) ( )] ( , , )} 0 0      t t x t F x x t x F      从以上讨论可以看出，不论边界情况如何，泛函极值都必须满足欧拉方程， 只是在求解欧拉方程时，对于不同边界情况，应采用不同的边界条件与横截 条件。 2.数学准备-泛函极值问题 0 0 x (t )  x f f x (t )  x f f x (t )  x 0 0     x t t F  0 0 x(t )  x   0   f x t t F  0 0     x t t F   0    f x t t F  0 0 x (t )  x  0    f x t t F  [ , , ]  0  f t t F x x t 0 0 x(t )  x ( ) ( ) f f x t  C t [ ( ) ( )]  0            f t t F x F c t x t    ( ) ( ) 0 0 x t   t f f x (t )  x [ ( ) ( )] 0 0            t  t t x t F x F     tf 固定 x(t0 )固定 x(tf)固定 x(t0 )自由 x(tf)固定 tf 固定 x(t0 )固定 x(tf)自由 x(t0 )自由 x(tf)自由 tf 自由 x(t0 )固定 x(tf )自由 x(t0 )固定 x(tf )约束 x(t0 )约束 x(tf )固定 无条件约束的泛函极值问题中的边界条件和横截条件列表

2数学准备-泛函极值问题 2数学准备-泛函极值问题 2数学准备-泛函极值问题 例2 求使性能密标 J-Pasgta h边界条作，)=C,》 i=a x(1)=a+b 为假小时的最优轨r间.设0=1.=C,C=2以t末给定. 与+1=2-4 解袋能长也号 ,= x F0-1+2 x0J=x《0)s=1,0=at*1 厥拉方程为： 横截条件 普-孟普=0 -m·儿 了=-+h=90 0- d「主 …时。 哥 1+F+…+ -0 +Fe· 解得(）1a=1 x()=1+1 2数学准备-向量泛函极值问题 2数学准备-向量泛雨极值问题 2.数学准备-有钓束条件的泛函极值问趣 在上面所时论约公式中，都假定x是1量。但是。所有会 对于始网时辣。和许鸡时封都给定时，横戴条骨 式幕可推广到峰变绿情况 置 赛精轻受装竿锅化.受 设性能密标J-广F:,i放 1.代数方程约来 x(t) 式中 设J-C4w 式中 )- 物来方程G(红，)-0。eRG。e:m<。 胸地W广泛通人-F,+2EGaw1。R“ 则玻拉方湿为菩一告瓷=0 对于末给定择端时辣时的横截条作为： 《1)给定始滨和择端有榨来： (2)给定锋和始有来 ◆地量函数任，意人)-Fx,)+2G(,) 式中 eo-r器儿 {二w-f 0. .=ra+sya+倍ya=0 分富职分 7

7 例2 求使性能指标 J x dt f t t   0 2 1 (1 ) 2  为极小时的最优轨线x*(t)。设x(0)=1，x(tf)=C(tf)，C(tf)=2-t, tf 未给定。 解 显然，所给出的性能指标就是x(t)的弧长，也就是说，要求从x(0)到直 线C(t)的弧长未最短。 t x(t) c(t) 2 x( 0) x*(t) x(t) 0 2 1 ( , , ) (1 ) 2 F x x t   x 欧拉方程为：   0     x F dt d x F  0 ( 1 ) 0 2 1 2            x x dt d   c 。 x x   2 1 (1 ) 2   2.数学准备-泛函极值问题 2 2 2 1 a c c x     x  a x (t )  at  b 这是一个x(t0 )固定，x(tf)约束情况下的极值问题。 由边界条件 x(t0 )=x（0）  b=1,x(t)=at+1 横截条件 [ ( ) ( )]  0            f t t F x F c t x t    (1 ) 0 (1 ) [ 1 ] 2 1 2 1 2                f t t x x x x     解得 x (t f )  1 a  1 x * (t )  t  1 。 t x(t) c(t) 2 x( 0) x*(t) x(t) 0 2.数学准备-泛函极值问题 由边界条件 ( ) ( ) f f x t  C t f f t 1  2  t 2 1 * t f  2 2 0 2 * * 2 1 2 1  (1 )   J x dt t x(t) c(t) 2 x(0) x*(t) x(t) 0 2.数学准备-泛函极值问题 在上面所讨论的公式中，都假定x是1维变量，但是，所有公 式都可推广到n维变量的情况 设性能指标 J F x x t dt f t t ( , , ) 0    式中              ( ) ( ) ( ) ( ) 2 1 x t x t x t x t n  则欧拉方程为   0     x F dt d x F  式中                              n x F x F x F x F  2 1 。                              n x F x F x F x F      2 1 2.数学准备-向量泛函极值问题 对于始端时刻t0 和终端时刻t f 都给定时，横截条件 ( ) 0 0    f t t T x F t   式中              ( ) ( ) ( ) ( ) 2 1 t t t t n     对于未给定终端时刻t f 时的横截条件为： （1）给定始端和终端有约束： [ ( ) ( )]  0            f t t T F x F c t x t    （2）给定终端和始端有约束 [ ( ) ( )] 0 。 0                    t  t T t x t F x F     2.数学准备-向量泛函极值问题 在实际问题中，对应泛函极值的最优轨线x*(t)通常不能任意选取，而受着 各种约束。求泛函在等式约束下的极值，称为条件泛函极值问题。 1.代数方程约束 设 J F x t x t t dt f t t [ ( ), ( ), ] 0    约束方程 G ( x , t )  0 n x  R m G  R m  n 构造增广泛函 J F x x t G x t dt T t t a f [ ( , , ) ( , )] 0      m   R 令纯量函数 L(x, x, ,t) F(x, x,t) G(x,t) T              0 0            J x x dt f t t T L T x L T x L  a      分部积分 2.数学准备-有约束条件的泛函极值问题

2数学准备-有约束条件的泛函授值向题 2数学准备-有约束条件的泛丽极值问题 2数学准备-有约束条件的泛函极值问题 上秘-4倍y+G'ah+了a=0 2:微分方程约来 3:积分方程约桌 最J-下，d 约来方型G-eGR”c为-常数 史锈登产。旅上试线之，度闲时满足下毯威拉方，的 设J一Fi陆 设2(t)▣G(x,,) 电￥件：G(x,,0-0.GcR- 则G(x,,)-2()-0 Z(t)-0 Zu,)-e 歌拉方程： 是-出是=0熹+(1-菩=0 设纯绿两数红，年石，)=F风红，名)+严Gx,主) 间 L=F+(G-2) 的来方根：G(￥，)。0 欧粒方程丝一圣各=0 拉方程普-兰兰=0一警-是鲁=0-0 横酸条作： (卧y6xk=0 ÷答+竖y-÷普-倍y1=0 的桌方程2)-G(3,,)Z0。》-0Zu,)-e 利用横截条件，根据始端状老心)阳许鸡状志x的不月情况，可以导 的束条情G(x,,)-0 横益务件 供Yk-0 出具修的迹界条件和横酸条件，其时论过程和结论与无的束条件的泛 保数条件 可昆，对干有的业条州的泛函经值问题。可采用妆麻朗日聚子法将其转化为无 两极物阿是和同。 (侍y6:=0s(s+年了作=0 密。在险条你议，业方微不多 3用变分法求解最优控制问题 3.用变分法求解最优控制问题 3.用变分法求解最优控制问题 设系统状志方程 一初始时刻及始端状态。哈定，给定，终端自由 可。受-r4,+受ra贸-0 构通增广泛稀 i-f八此，) 为使上式成立，应同时满足下列方程 能指标J一电，A]F油 .-,小'F,+V红4-d 表方8作鞋方同要 令哈击尔顿两数： 状志方程 毁 式中R。B解为纯绿雨最 H品么0-F+f4,a) 控制方程 0… 量优控刺闻愿就是寻求最优控制')及量优状态轨连” 则上-，M-%,20-2 机酸条丹 尝-好4心 使性能需标取餐值 岛尝学r+尝-0r-a-轴0 注意孙： 小 ga袖-中-文亚袖，-● 对于丙编圆定的情况下精截条件心一。，一 8

8         0 0 0            f f t t T x L t t T T x L dt d T x L x G  dt x   由于δx, δλ相互独立，为使上式成立，应同时满足下述欧拉方程，约 束方程和横截条件： 欧拉方程：   0     x L dt d x L       0       x F dt d T x G x F    约束方程： G ( x , t )  0 横截条件：   0 0    f t t T x L  x  利用横截条件，根据始端状态x(t0 )和终端状态x(tf)的不同情况，可以导 出具体的边界条件和横截条件，其讨论过程和结论与无约束条件的泛 函极值问题相同。 2.数学准备-有约束条件的泛函极值问题 2：微分方程约束 设 J F x x t dt f t t ( , , ) 0    约束条件：G ( x , x, t )  0 m G  R 设纯量函数 L(x, x, ,t) F(x, x,t) G(x, x,t) T        欧拉方程   0     x L dt d x L           0           T x G dt d x F dt d T x G x F   约束条件 G ( x , x , t )  0 横截条件   0 0    f t t T x L  x     0 0       f t t T x T G x F   x   2.数学准备-有约束条件的泛函极值问题 3：积分方程约束 设 J F x x t dt f t t ( , , ) 0    约束方程 G x x t dt c f t t   ( , , ) 0  m G  R c为一常数 设 Z (t ) G ( x , x, t )   则 G ( x , x, t)  Z (t)  0 ( ) 0 Z t 0  Z t c ( f )  令        z x x        z x x    L F (G Z) T      欧拉方程   0     x L dt d x L     0     x L dt d x L    0  约束方程 Z (t ) G ( x , x, t )   Z (t 0 )  0 Z t c ( f )  横截条件   0 0    f t t T x L  x  可见，对于有约束条件的泛函极值问题，可采用拉格朗日乘子法将其转化为无 约束条件的泛函极值问题进行求解。在不同边界条件情况下，欧拉方程不变， 只是边界条件及横截条件不同。 2.数学准备-有约束条件的泛函极值问题 设系统状态方程: x  f (x,u,t) 性能指标:    f t t f f J x t t F x u t dt 0 [ ( ), ] ( , , ) 式中 n p x  R u  R  和F为纯量函数 最优控制问题就是寻求最优控制 ( ) * u t 及最优状态轨迹 ( ) * x t 使性能指标J取极值. 3.用变分法求解最优控制问题 一.初始时刻 及始端状态 给定 t0 x(t0 ) , t f给定,终端自由 构造增广泛函      f t t T a f f J x t t F x u t f x u t x dt 0 [ ( ), ] { ( , , )  [ ( , , ) ]} 令哈密尔顿函数: H (x,u, ,t) F(x,u,t) f (x,u,t) T     则     f t t T J a x t f t f H x u t x dt 0 [ ( ), ] [ ( , ,, )  ] ( ) [( ) ( ) ( ) ] 0 0                  x x dt H u u H x x H x x J T T T T T t t t t T a f f            注意到:     f f f t t t T t T t t T xdt x xdt 0 0 0          x (t 0 )  0 3.用变分法求解最优控制问题 ( ) [( ) ( ) ( ) ] 0 0                   x dt H u u H x x H x a x J T T T t t t t T f f            为使上式成立,应同时满足下列方程: 欧拉方程(伴随方程) x H       状态方程     H x 控制方程  0   u H 横截条件 f f f t t t T x t x t x x x               ( ) ( ) ( ) 0 0 0 对于两端固定的情况下横截条件 f f x(t )  x , x(t )  x 0 0 3.用变分法求解最优控制问题

3.用变分法求解最优控制问题 3用变分法求解最优控制问题 3用变分法求解最优控制问题 例1 授系统状志方程为 主()=-0+) i-x-2 跗 二.初始时刻1及始端状态4)给定，1y给定终端约束 0的垃界条作为0-l北，-0 克55-w0+ 设许瑞的来方程为，1-，月-0MGR 求最优校制)使下列作伦密标 -6E百5a0o, 构造州广泛： J'+恤 人.-，月+PM,月+了红此+V红，k-d 为最小 由边舞保作可0-1中，》-0 解作哈密尔顺雨数日-++水-+ 0-E:业点w5 =+M,+广H,-d 聚拉方根-翌 -4 式神E时 无▣-x+无 修制 控制方程 u+人m0 2a.e,E465 =0 1 状志方程 ,-x+■ 5-eBEw 取极植的必要条件是 3.用变分法求解最优控制问题 3.用变分法求解最优控制问题 3.用变分法求解最优控制问题 正剩方程 状态方程 三初始时刻。及始端状态心，)给定，1，自由，终端约束 用变分法求解最优解的必要条件： 设体端的来为，1-0 藏拉方型 胸造增广泛两J.-可电，M,小+电，，小+1Hx,2- 性能指标J-e1u,h,1小F,恤 控制方程 熙… 园。一0得取极慎的冬要条件本 H,,0-F《a,,0+21,0 正则方程 边条和精截条件化。)-，，月-0 拉防程要0 系埃方程-八红，， ,-喂尝 盛-，w小0 约来条件4-，M,h,1-0 ,尝尝 五到方81 g 尝… 控刺方程 … 9

9 例 1 设系统状态方程为 x（t） x(t)  u(t) x(t) 的边界条件为 x(0)  1, x(t f )  0 求最优控制 u(t) 使下列性能指标    f t J x u dt 0 2 2 ( ) 2 1 为最小 解: 作哈密尔顿函数 ( ) ( ) 2 1 2 2 H  x  u   x  u 欧拉方程    x   控制方程  0,   0   u  u H 状态方程 x x u H x        ,   x H       3.用变分法求解最优控制问题             x x x   ( ) (0) 2 2 1 [( 2 1) ( 2 1) ] (0) 2 2 1 2 2 2 2  t t t t x   e   e x  e  e   [( 2 1) ( 2 1) ] (0) 2 2 1 ( ) (0) 2 2 1 2 2 2 2   t t t t  e  e x   e   e   消除u 由边界条件 x(0)  1, x(t f )  0 f f f f t t t t e e e e 2 2 2 2 ( 2 1) ( 2 1) (0)         得最优控制 [( 2 1) ( 2 1) ]} ( 2 1) ( 2 1) { 2 2 1 2 2 2 2 2 2 2 t t t t t t t t e e e e e e e e u f f f f                                         x x   1 1 1 1   3.用变分法求解最优控制问题 二. 初始时刻 及始端状态 给定 0 , 给定,终端约束. t ( ) 0 x t f t 设终端约束方程为 M[x(t f ),t f ]  M[x(t f )]  0 q M  R 构造增广泛函:       f t t T f T J a x t f v M x t F x u t f x u t x dt 0 [ ( )] [ ( )] { ( , , )  [ ( , , ) ]}      f t t T f T f x t v M x t H x u t x dt 0 [ ( )] [ ( )] { ( , ,, )  ]} 式中 q v R 0 [ ( ) ] [( ) ( ) ( ) ] 0                      x dt H u u H x x H v x x M x J T T T t t t t T T a f f           J取极值的必要条件是 3.用变分法求解最优控制问题 正则方程             欧拉方程 状态方程 x H H x     控制方程  0   u H 边界条件和横截条件 ( ) , 0 0 x t  x [ ( )]  0 f M x t f t t T f v x M x t       ( )  [ ( ) ]   3.用变分法求解最优控制问题 三. 初始时刻 及始端状态 给定 t0 x(t0 ) , t f 自由,终端约束 设终端约束为 M[x(t f ),t f ]  0 构造增广泛函      f t t T f f T J a x t f t f v M x t t H x u t x dt 0 [ ( ), ] [ ( ), ] [ ( , ,, )  ]  0 a J 得J取极值的必要条件为: 正则方程               x H H x     控制方程  0   u H 边界条件和横截条件 ( ) , 0 0 x t  x M[x(t f ),t f ]  0 f t t T f v x M x t       ( )  [ ( ) ]   [ ]  0        f t t T t M v t H  3.用变分法求解最优控制问题 用变分法求解最优解的必要条件: 性能指标    f t t J x t f t f F x u t dt 0  [ ( ), ] ( , , ) H (x,u, ,t) F ( x,u,t) f ( x,u,t) T     系统方程 x  f (x,u,t) 约束条件 ( ) , 0 0 x t  x [ ( ), ]  0 f f M x t t 正则方程    H x x H      控制方程  0   u H 3.用变分法求解最优控制问题

条作边界条料和横戴条件 终端因定 3.用变分法求解最优控制问题 3.用变分法求解最优控制问题 终端自由 ,”品 例2已知系统找志方程为-0，o-】 0)-4eh6e 给定 终端钓束 g川-0，-尝· 求最优拉制：')使怪能指标了一心产(2+产边为最小 解本题为，给定，裤漏自由的销况 -i---- 终端因定 ”哥 边界条外与横鼓条料 H-e22◆2+2出 小山小”部0-。 终端自由 6》-x , 等 求得 i-v 5-1 t E+e6 i-22 6"不5-平“5-+w 自由 ,= ,,1-0 终端钓束 西 拉防程兴。 242a2-0→i-22w+i 最得级执拉制0广不E-。 -2x0--22u+w2 --l.7957ea-00591ena] 消至+2近-x-0 3用变分法求解最优控制问题 3.用变分法求解最优控制问题 3.用变分法求解最优控制问题 例3 慢不统的状老方程为 垃界采桥和横醛条科 H-2++4-+ -名 正防程”股名山。+ 0)-0+0.56-6+5-0 24-+4 40-e-0-*6 一-3卡4 -4-0.5名46-0 10明-0-0 与4-e-0-5 02-a-f 性能指标一2-开+24-油 BM 0-2-f-2乎 择端的来条件(2)+5红2-15 4m6 M-，2+524-15-0 4,i', M-24s,(4-15=0 认求使J一m的量优控制 控制方程 尝0+40小 2(2)-2-54-4 解本题为一始定锋端受均来的敏忧解例圆 20 U 2)--4:)+g u"+0 …++5+时 8-2+- 40-60-0 2(2)=x:(2)-2+5n°ce2+9, 2以-4吗+4 M-42)+52)-15=0 40ee-4+ 代队2.x2) 10

10 条件边界条件和横截条件 t f 给定 终端固定 终端自由 终端约束 t f 自由 终端固定 终端自由 终端约束 ( ) , 0 0 x t  x f f f M[x(t )]  0  x(t )  x 0 0 x(t )  x ( ) ( ) f f x t t      0 0 x(t )  x 0 0 x(t )  x 0 0 x(t )  x 0 0 x(t )  x [ ( )]  0 f M x t f t T f v x M x (t ) [ ( ) ]         f f x(t )  x f f t H t      ( ) ( ) ( ) f f x t t      f f t H t      ( ) M[x(t f ),t f ]  0 f t t T f v x M x t       ( )  [ ( ) ]   f t t T f t M v t H t       ( )  [ ]  例2 已知系统状态方程为 x  u(t), x(0)  1 求最优控制 ( ) * u t 使性能指标    1 0 2 2 2 J e (x u )dt t 为最小 解 本题为 f t 给定，终端自由的情况 H e x u u t  (  )   2 2 2 正则方程:    H x x H      控制方程  0   u H 得 x  u t xe2   2  t t ue u u e 2 2 2 0 2(2 )         t t xe u u e 2 2  2  2(2  ) 消除u x 2x  x  0 3.用变分法求解最优控制问题 t t x t c e c e (1 2) 2 (1 2) 1 ( )       t t u x c e c e (1 2 ) 2 (1 2 ) 1 (1 2) (1 2)            边界条件与横截条件 0 0 x(t )  x (0) 1, (1) 0 ( ) ( )          x x t t f f 求得 2 2 1 ( 2 1) ( 2 1) 2 1       e c 2 2 2 2 2 ( 2 1) ( 2 1) ( 2 1)        e e c 最后得最优控制 [ ] ( 2 1) ( 2 1) 1 ( ) (1 2) 2 2 (1 2 ) 2 2 * t t e e e e u t              1.7957[ 0.0591 ] 2.4142 t 0.4142 t   e  e  3.用变分法求解最优控制问题 例3 设系统的状态方程为 1 2 x  x x  x  u 2 2  x1 (0)  0 x2 (0)  0 性能指标       2 0 2 2 2 2 1 2 1 [ (2) 2] 2 1 [ (2) 5] 2 1 J x x u dt 终端约束条件 x1 (2)  5x2 (2)  15 试求使 J  min 的最优控制 解 本题为 t f  2给定 终端受约束的 最优解问题 ( ) 2 1 1 2 2 2 2 H  u   x   x  u u x u 1 2 2 2 2 ( ) 2 1        2 2 2 1 [ (2) 2] 2 1 [ (2) 5] 2 1   x   x  M  x1 (2)  5x2 (2) 15  0 3.用变分法求解最优控制问题 正则方程 x x x x u H x         1 2 2 2   ,   1 1 1 1 1 , 0, (t) c x H x H                   2 1 2 2 1 2 2 , (t) c e c x H t              控制方程 2 2 1 0 u 0 u(t) c e c u H t            x 2 (t )   x 2 (t )  u 2 3 2 1 2 1 x (t) c e c e c t t     1 3 2 1 4 2 1 x (t) c e c e c t c t t       ( ) 2 1 1 2 2 2 2 H  u   x   x  u u x u 1 2 2 2 2 ( ) 2 1        2 2 2 1 [ (2) 2] 2 1 [ (2) 5] 2 1   x   x  M  x1 (2)  5x2 (2) 15  0 3.用变分法求解最优控制问题 边界条件和横截条件 (0) 0, 0.5 0 x    c2  c3  c4   c1  0.5c2  c3  0 ) ( ) ( ) ( ( ) ( ) 1 1 1 f T f f f v t x t M x t t         1 1 1  (2)  x (2)  5  v  c ) ( ) ( ) ( ( ) ( ) 2 2 2 f T f f f v t x t M x t t         1 2 2 2 2  ( 2 )  x ( 2 )  2  5 v  c e  c 代入 (2), 1 x ( 2 ) 2 x 2 3 2 1 2 1 x (t) c e c e c t t     1 3 2 1 4 2 1 x (t) c e c e c t c t t       2 2 2 1 [ (2) 2] 2 1 [ (2) 5] 2 1   x   x  M  x1 (2)  5x2 (2) 15  0 3.用变分法求解最优控制问题