
第2章失餐场的微分运算 7 y-xsi血f+ycos0 (2.19) 如果任何一对数字在用这些方程进行变换时,其方式与云和y的变换方式一样,那么它们便 是一个矢量的分量. 现在让我们来看看如图26(b)所选取的那两个邻近点P:和P,上的温度差.若我们 按x和y的坐标计算,该可以写成 -器血 (2.20) 因为刨等于零 在那个加撒的系统上进行计算,应该得出个什么呢?我们必须写出 n-+84. a (2.21) 看-一看图26(6),即可见 4z'=4r 00s (2.22) dy'=-4r sin 0, (2.23) 因为当c为正时为负.把这些代入式(2.21)中去,得: Ar sin (2.24) (2.25) 比较式(2.2)和(2.20),我们得到 -0-血 (2.26) 这个式说明:r/z可从P/x和P/时获得,正如同式(2.18)中的x可以从x和寸获 得那样.因此P/就是一个矢量的分量.同样的论据也该可以证明,/y和P/z 分别为它的和:分量.所以T肯定就是一个矢量,它是从标量场T导出来的一个矢 量场. §2-4算符V 现在我们就能够做出一件非常有趣而又巧妙的事情一并且是使数学绚丽多采的一些 事物的标志.上面对T的陡度或T是一个矢量的论证,并未与我们究竟是在对哪一个标 量场进行微分有关。假若T是由任一种标量场来代替,所有论证也该同样进行.既然不管 我们对之进行微分的是什么,那些变换公式都相同,那就满可以略去T而由一个算符方程 式来代替式(2.26): (2.27) 正如琼斯(Jeans)曾经说过的那样,我们留给算符去“忙于对某一件东西取微分”. 由于这些微分算符本身就已如同一个矢量的分量应该变换的那样进行变换,我们便可 以称之为一个矢量算符的分量,即可以写成: a aa -(品需品) (2.28) 那当然就是意味着

18 费曼物理学讲义(第二卷) (2.29) 已经把T除去而抽象出陡度来了一这是一个绝妙的主意. 当然,你必须始终记住了是个算符.它单独没有什么意义.如果又本身没有什么意 义,那么要是我们乘以一标量一比如T一那乘积T下又会有什么意义呢?(我们总可以 对一失量乘以一标量.)它仍然不具有什么意义.它的工分量是 (2.30) 它并非一个数值,而仍然是某种算符.然而,按照矢量代数,我们仍可以把TT叫作一个矢 量 现在让我们在7的另一边乘以一标量,使之形成乘积()。在一般代数中 TA-AT, (2.31 但我们得要记住,算符代数稍有别于一般的失量代数.用算符时,我们必须时刻保持正确顺 序,以便使算符能够构成适当意义,如果你只是记住算符V会服从与微商记法相同的惯例, 那你就不会有任何困难。凡想要微分的东西一定要放在7的右边。这里,先后次序是重要 的 牢记这个次序问题,我们就懂得了TT是一个算符,但T却不再是一个饥饿的算符 该算符已完全满足了.并且它确实是一个具有意义的物理矢量.它代表了T的空间变率。 P的分量,就是在如方向上T变化得多快。究竞失量T的方向指向哪里呢?我们知 道,在任一方向上,T的变率等于VT在该方向的分量(见式2.16).由此可以推知,T的 方向应该是那个具有尽可能大的分叠的方向—一换句话说,其中T变化得最快的方向。T 的陡度具有(在T上的)最陡峭的斜率的方向. 825V的运算 矢量算符又,能否作其他方面的代数运算?如把它同一个矢量连结起来.可以通过点 乘来连结两个矢量,这可构成这样两种点积: (矢量)或7…(矢量). 这第一个还没有什么意义,因为它仍然是一个算符.最终的含意取决于它所运算的对象如 何.那第二个乘积则是一个标量场.(4B总是一个标量.) 让我们就用一个熟悉的矢量场、比如k,来试试它与又的点积吧.把它写成分量式: V.h-Vha+V/i,+7.ha (2.32) 或 h-陪+警+路 (2.33) 这个和式在坐标变换之下是不变的。假如我们选释一个不同的坐标系(通过加嫩来表明), 则我们会有” k-驰++0, (2.34) 这个值应该与从式(2.33)所得的相回,虽则看起来是不同的.这就是说,对于在空间每一点, ·我们把h设想成一个取决于空间位置的妆理悬,而不是把它设想成一个严格的含有三个自变量的数学函数,当A 对于云、从、或对于公、、。取微分时,4的数半表式过必须先表达为各该自变量组的函数

第?章失量场的微分运到 19 v.h-V.h. 2.35) 因此,了,确是一个标量场,它必须代表某一物理量.你应当体会到,在了,k中,各微商的 结合方式相当特殊.此外,还有许多象h,/c的其他各种结合,那既不是标量,也不是矢量 的分量 标量7(矢量)在物理学中非常有用.它的名称叫做散度.例如, 7,h-divh-rh的散度”. (2.361 就象在上面我们对VT所做的,也可以赋予了一个物理意义.然而,我们将把这项工作 推迟到以后。 首先,我们愿意来看看,是否还有别的东西可以由矢量算符又得到的?我们应当指望 会有这么一种东西: V×h=一个矢量. (2.37) 它是一个矢量,其分量可按照有关叉积的通常规则(见式2.2)来写出: (2.38) 同理, x-hA-跨-器 (2.39) (x,-h-a-0-0 (2.40) 下×h这个结合式叫做h的旋度”.其定名原因及其物理意义都将在以后讨论。 综合起来,同V的结合总共有三种: vT=gradT-失最; V.h=divh+标量: V×h=curlk=矢量. 利用这些结合,就可以按照一种方便方式—一种并不依赖于任一特定坐标轴组的普遍方 式 来写出关于场的空间变化. 作为对失量微分算符又应用的一个例子,不妨写出曾在第一章中用语言表达的那些电 磁定律内容相同的一组失量方程.它们称为麦克斯韦方程组。 麦克斯韦方程组: (四B-6 阅xB-盟 (2.41) (3)7.B=0 国7×B=票+号 式中,ρ代表“电荷密度”,即每单位体积的电量;了代表“电流密度”,即每秒流经单位面积的 电荷流率.这四个方程式包含电磁场的全部经典理论.我们将看到,采用这一套新的记法, 将会得到多么优美而又简洁的形式!
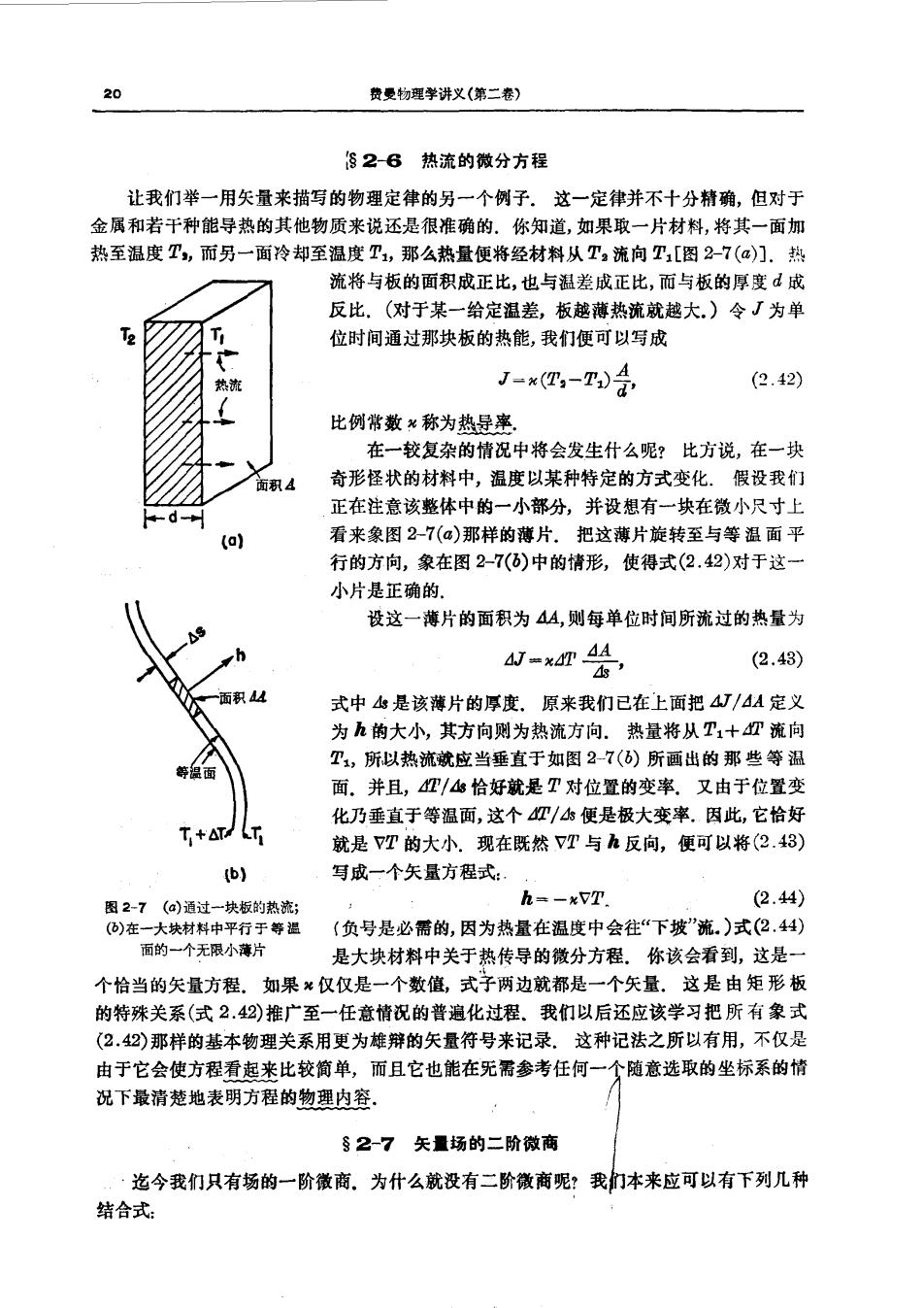
20 费受物现学讲义(第二春) 26热流的微分方程 让我们举一用矢量来描写的物理定律的另一个例子。这一定律并不十分精确,但对于 金属和若干种能导热的其他物质来说还是很准确的.你知道,如果取一片材料,将其一面加 热至温度T,而另一面冷却至温度T,那么热量便将经材料从T。流向T1[图2-7(⑧)门.热 流将与板的面积成正比,也与温差成正比,而与板的厚度d成 反比.(对于某一给定温差,板越薄热流就越大.)令J为单 位时间通过那块板的热能,我们便可以写成 J=四,-T) (2.42) 比例常数%称为热导率 在一较复杂的情况中将会发生什么呢?比方说,在一块 面积4 奇形怪状的材料中,温度以某种特定的方式变化.假设我们 正在注意该整体中的一小部分,并设想有一块在微小尺寸上 (1 看来象图2-7(c)那样的薄片.把这薄片旋转至与等温面平 行的方向,象在图2-7()中的情形,使得式(2.42)对于这 小片是正确的 设这一薄片的面积为44,则每单位时间所流过的热量为 (2.43) 式中s是该薄片的厚度.原来我们已在上面把4J/4A定义 为h的大小,其方向则为热流方向.热量将从T1+垭流向 T,所以热流就应当垂直于如图2-7(6)所画出的那些等温 面.并且,P/恰好就是T对位置的变率.又由于位置变 化乃垂直于等温面,这个/s便是极大变率.因此,它恰好 就是7T的大小.现在既然7T与h反向,便可以将(2.3) (b) 马成一个矢量方程式 h=一VT 图2-7(@)通过-一块板的热流 (2.44) (负号是必需的,因为热量在温度中会往“下坡”流.)式(2.44) 是大块材料中关于热传导的微分方程.你该会看到,这是 个恰当的矢量方程.如果%仅仅是一个数值,式子两边就都是一个矢量.这是由矩形板 的特殊关系(式2.42)推广至一任意情况的普遍化过程.我们以后还应该学习把所有象式 (2.42)那样的基本物理关系用更为雄辩的矢量符号来记录.这种记法之所以有用,不仅是 由于它会使方程看起来比较简单,而且它也能在无需参考任何一个随意选取的坐标系的情 况下最清楚地表明方程的物理内容。 §2-7矢量场的二阶微商 迄今我们只有场的一阶徽商。为什么就没有二阶徽商呢?我们本来应可以有下列几种 结合式:

第名章矢量场的微分运算 21 (a)v.(T): (b)V×(r): (o)7(h): (2.45) (d)v.(×h): ()V×(×). 你可以核实一下,这些是所有的各种可能结合」 让我们首先看一看那第二个式(b).它与下式有相同形状: A×(AT)=(A×A)T=0. 因为A×A总是等于零.因此,我们就应该有: ourl(grad T)-V×(T)=0 (2.46) 如果用分量来计算一遍,便可以看出这个式是怎样产生的: v×(四.-.(四,-,(m,是(买)-(C)》 (2.47) 这会等于零(根据式2.8).对于其他分量也是如此.因此,在任何一种温度分布中(实际上, 对于任何一个标量函数),始终是V×(T)=0. 现在让我们来取另一个例。试看能否找到另一个零.一个矢量与一个其中含有该矢量 的矢积点乘的结果为零,即 A(A×B)=0, (2.48) 因为AXB垂直于A,所以在A方向上就没有AXB的分量.与此相同的一种结合出现 在式(2.45)(d)上,因而我们有: v,(×h)=div(c如rlh)=0. (2.40) 再次用分量进行运算来证明上式为零并不困难。 现在我们将不加证明地陈述两个数学定理.它们是物理学家亟待了解的十分有趣而又 有用的定理。 在一个物理问题中,我们经带会发现某一个量 一比如矢量场A一的旋度为零.如 我们由式(2.46)就看到,一个陡度的旋度为零,这是很容易记住的,因为矢量的特性就是这 样.于是,肯定有可能A本来就是莱一个量的陡度,这样它的旋度才必然等于零.这个有 趣的定理说明,如果culA等于零,则A总是某种东西的陡度 一始终会存在某一标量场 中使得A等于grad中.换句话说,我们有这样一个 定理: 如果V×A=0, 就有一个功 使得A=中: (2.50) 当A的散度为零时,还有一个相似定理.从式(2.49)我们看到,某种东西的旋度之散 度总是零.如果你遇到ivD为零的一个矢量场D,那你就可以下结论说,D是某一矢量 场C的旋度。 定理: 如果7·D=0, 就有一个C