
2 矢量场的微分运算 §2-1对物理学的理解 对物理学家来说,要有从各不同观点去看问题的技巧.因为对实际物理问题的准确分 析往往非带复杂架,任一特定物理情况都可能因过于复杂,以致不能直接通过解微分方程来进 行分析.然而如果人们对于在不同情况下解的特性有某种感触,则对于一个系统的行为仍 可以获得十分良好的概念.如场线、电容、电阻以及电感等概念,对此目的来说都是十分有 用的.因此,我们将花不少时间来进行分析.通过分析,对于在不同情况下所应当发生的事 情我们就会获得一种感觉.另一方面,在比如说场线这类启发式模型中,却没有一种会对所 有情况都是真正充分和准确的,只有一种表达定律的准确方式,那就是通过微分方程.因 为微分方程具有下述两个优点,它既是基本的,就我们所知又是准确的。如果你已学习过那 些微分方程,便可以经常回去复习查对,就不必再重新学习的了 要了解在各种不同情况下会发生什么事情,这将花费你一些时间.你必须求解那些方 程.每次解方程时,就将对解答的性质有所体会。为了把这些解答牢记在心,利用场线及其 他概念来研究解答的意义也是有益的.这就是你将确实“理解”方程式的途径.这也是数学 和物理学的区别所在。数学家,或者具有十分数学修养的人,在“研究”物理学的过程中往往 由于看不见物理学而误入歧途。他们说:“看,这些微分方程一一麦克斯韦方程组一一就是 电动力学的一切;物理学家已经承认,没有什么东西不包含在这些方程式之内了.这些方程 尽管复杂,但毕竞不过是一些数学方程式,要是我能在数学上对它们里里外外都理解透,那 我对物理学也就理解得透彻了”.可惜,事实却并非如此。大凡抱着这种观点研究物理学的 数学家一也确实有不少这样的人一一往往很少会对物理学作出什么贡献,而实际上对数 学的贡献也很可怜。他们之所以失敗,是由于现实世界的实际物理情况意会那么复杂,以致 需要对方程式县有远较为广泛的理解 确实理解一个方程式一 一即不仅在严格的数学意义上的理解一意味着什么,狄喇克 对此就早有所评述,他说:“如果无靥实际解一个方程面对于解答的特性已有二种估计办 法,那我就算已懂得了该方程式的意义.”因此,若我们无需实际解那个方程组而对在特定情 况下会发生什么便已有一种了解的办法,则我们便算“理解”了应用到这些情况上去的那个 方程组了,物理上的理解乃是一种完全非数学性的、不准确的、亦并非严格的东西,但对于 个物理学家来说却是绝对必需的 照常规说,象这样一种课程是通过物理概念的发展过程一即从简单的情况开始逐渐 过渡到越来越复杂的情况 一来编排的.这就要求读者要不断忘记以前所学到的一忘记 在某些情况下正确,而在一般情况下却不正确的那些东西.例如,电力取决于距离的平方那 一条“定律”就不是一贯正确的.而我们在本书中宁可取相反的途径。一开始我们就讨论那 些完整定律,然后才回过头来把它们应用于一些简单情况,从而在这些过程中发展物理概 念。这就是我们将要做的事情

第召章失量场的嫩分运算 13 我们所采取的途径与历史的途径完全相反,人们在后一途径中是用从中获得知识的各 种实验来发展这一过程的.但物理学这一学科在过去约二百年中是由一些十分有发明天才 的人们发展开来的,面如果我们仅以有限时间就要获得我们的知识,那就不可能包括他们曾 经做过的一切事情。可借的是,在这些讲课中我们很可能会丢失的东西之一就是这个历史 的、实验的发展方面.希望在实验室中这个缺陷能够得到某些弥补.你也可以通过阅读大 英百科全书来补充我们所不得不割爱的东西,那里载有一些卓越的历史性专题,涉及电学 及物理学其他部分。你也可以在有关电磁学的许多教科书中找到一些历史知识. §2-2标量场和矢量场一T与h 现在我们要从电磁理论的那种抽象的、数学的观点开始。目的是为了解释第一章中所 给出的那些定律的意义。而要做到这一点,我们必须首先对一种将要用到的崭新而又特殊 的记法加以解释所以就让我们暂时忘却电磁学而转过来讨论矢量场的数学.这不但对于 电磁学而且对于所有各种物理情况都是十分重要的.正如通常微积分学对于所有各物理部 门都那么重要一样,矢量的微分学也是如此.现在我们就转到这么一个课题上来吧。 下面列举一些来自矢量代数的若干项事实,并假定你们都已经学过了. AB-标量-A,B十A,B十A,B。 (2.1) A×B=矢量 (2.2) (A×B).=A,B,-A,B (A×B)=AB.-AB, (A×B)w=AB。-AB A×A=0 (2.3) A.(A×B)=0 (2.4》 A.(B×C=(A×B)C (2.5 A×(B×C)=B(AC)-C(AB) (2.6 我们也要用到从微分学方面得来的下列两个等式: 4f%,g+影4+影 (2.7) 器 (2.8) 这里,第一个等式(27)当然只有当血、似、血都趋于零时才正确. 最可能简单的一种物理场是标量场。你应当记起,我们所说的场是指取决于空间位置 的一个量.所谓标量场,是指每点仅由一个单独数量一一个标量一所标志的那种场」 当然这个数量还可随时间而变,但眼前我们还无需为此操心。我们将只谈论在某一特定时 刻,场看来是个什么样子.作为标量场的一个例子,试考虑一块固体材料,其中某些地方受 热而另一些地方受冷,使得该物体的温度以一种复杂方式逐点改变,于是湿度将是从某 直角坐标系上量得的代表空间每一位置(,头,)的函数.可见温度是一标量场. 考虑标量场的一种办法是去设想一些“恒值面”,即将所有具有相同场量的点都连接起 来而成的一些想象中的面,正如在地图上那些由等高点连成的等高线一样对于一个温度 场来说,这些恒值面被称为“等温面”或等温线.图2-1表示一温度场,并表明在?-0处T
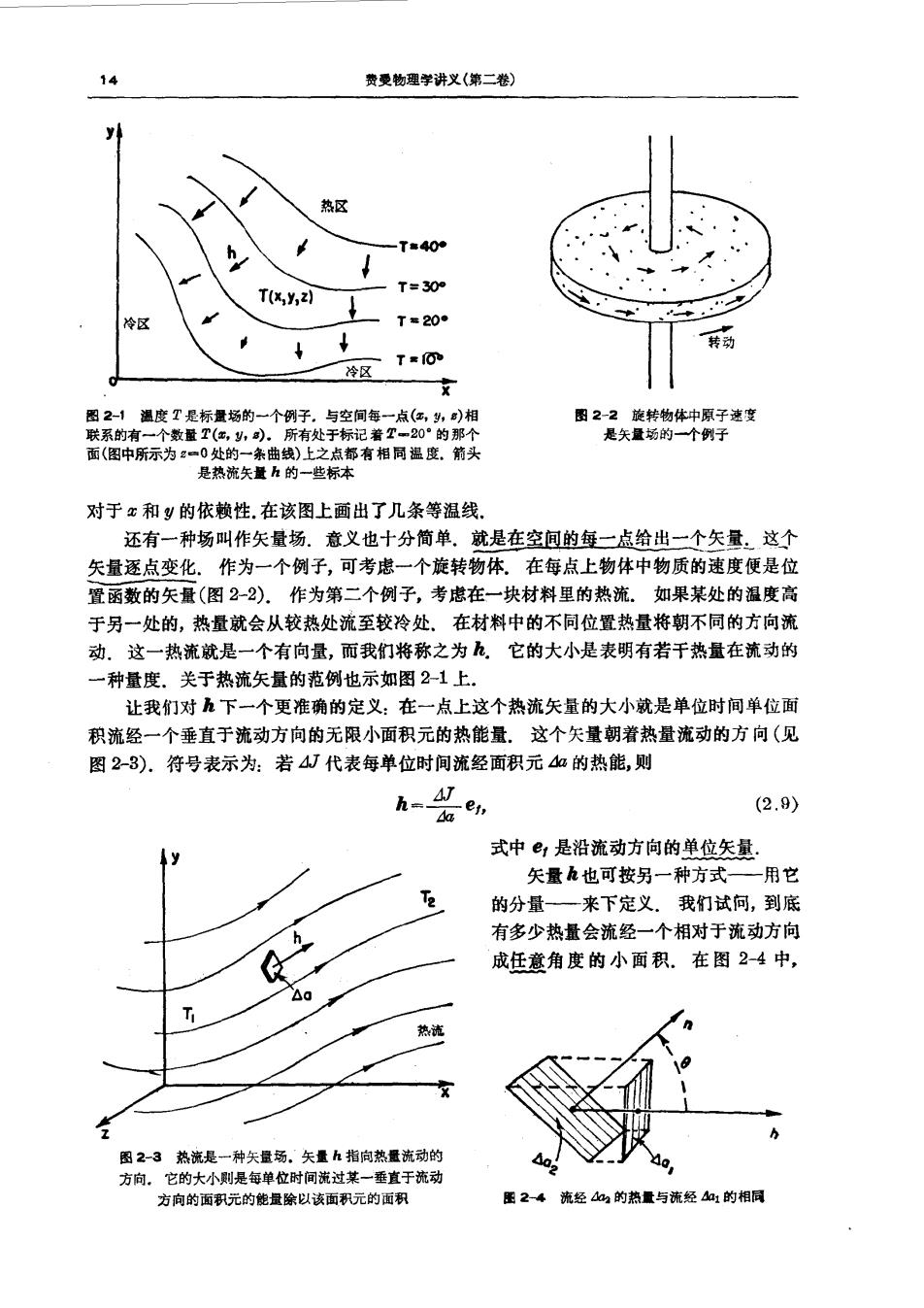
14 费受物理学讲义(第二卷) T(y,2 T- 对于x和y的依赖性.在该图上画出了几条等温线. 还有一种场叫作矢量场.意义也十分简单.就是在空间的每一点给出一个失量,这个 矢量逐点变化.作为一个例子,可考虑一个旋转物体.在每点上物体中物质的速度便是位 置函数的矢量(图22).作为第二个例子,考虑在一块材料里的热流。如果某处的温度高 于另一处的,热量就会从较热处流至较冷处.在材料中的不同位置热量将朝不同的方向流 动.这一热流就是一个有向量,而我们将称之为几.它的大小是表明有若干热量在流动的 一种量度关于热流矢量的范例也示如图21上 让我们对h下一个更准确的定义:在一点上这个热流矢量的大小就是单位时间单位面 积流经一个垂直于流动方向的无限小面积元的热能量.这个矢量朝着热量流动的方向(见 图2-3).符号表示为:若4J代表每单位时间流经面积元4a的热能,则 (2.9) 式中是沿流动方向的单位矢量, 失量九也可按另一种方式—用它 的分量一来下定义.我们试问,到底 有多少热量会流经一个相对于流动方向 成年意角度的小面积.在图24中, 热清 图23热流是一种矢量场,矢量h指向热量流动的 方向。它的大小则是每单位时间花过某一垂直于流动 方向的面积元的能显除以该面积元的面积 匪2-4流经a购的热量与流经的相同

第2章失量场的微分运舞 15 我们所表示的一个小面积,与垂直于热流的另一个小面积4a1作成某一角度.单位矢量 n与面积da,垂直.n与h之间的角度就等于该两面积间的角度(因为k垂直于a).那 么,每单位面积流经4a,的热量有多少呢?流经a,的热量就等于流经4a,的,只不过面积 不同罢了.事实上,4a1=a2co8日.因此,流经a,的热流就是 diaoos 0h.n. (2.10) 我们就此式加以注解:流经任何垂直于单位法线?的面积的热流(单位时间、单位面积)为 hn.同样,我们也可以说:垂直于面积元a,的热流分量为.如果我们愿意,也可以 认为这些说法定义了.我们也将把这些相同概念应用于其他矢量场. §2-3场的微商—陡度 当场随时间变化时,可通过给出场对时间的微商来加以描述。我们希望也按同样办法 来描述场对空间的变化,因为对于例如在一点上的温度与在某一邻近点上的温度间的关系, 我们是感兴趣的.怎样求得温度对位置的微商呢?是否应该对求温度的微商?还是对 y,或是对? 有用的物理定律应当不依赖于坐标系的取向。因此,它们应被写成两边都是标量或两 边都是失量的一种形式.一个标量场的微商,比如说T/,究竟是什么呢?是标量,还是 矢量,或还是其他什么东西?它并不是标量,也不是失量,因为正如你能容易领会的,假如取 另一条x轴,肯定T/x就会改变.可是要注意,微商可能有三个:T/z迎/y和沉/z. 由于有这三种微商,而我们又知道要形成一失量需要三个数量,也许这三个微商就是一个矢 量的分量吧: (器器上失量 (2.11) 当然,一般并非任何三个数量都能构成为一矢量的.只有当我们旋转坐标系,矢量的各 个分量按照正确的方式变换时,这才成立,所以需要分析坐标系旋转时,这些徽商究竟是如 何变换的.我们将证明(2.11)确实是一个矢景。 当坐标系转动了某一角度,这些微商的确 会按正确的方式变换 我们可以从几方面看到这一点.一个途径是,提向的答案是一个与坐标系无关的问题, 而试图用“不变量”的方式来表达这一答案.例如,若S-AB,而且若A和B都是失量, 则我们知道 因为我们已在第一卷第十一章中加以证明一8就是一个标量.不须去审 查是否会随坐标系改变而改变,我们就已知道了8是一个标量.改变是不可能的,因为它是 两个矢量的标积.与此相仿,如果我们知道A是一矢量,而我们又有三个数B:B,、B,并 目找出 A:B1+AyB2+A.B3-S, (2.12) 式中S是对于任何坐标系都相同的数值.那么,这三个数B、B:、B,就应该是某一矢量B 的分量B、B、B了 现在让我们想一想温度场.假设取P1和P,两点,它们之间有一微小距离4R.在P, 上的温度为T而在P,上的为T,彼此间的差值T-T,-T.在这些实际的物理点上温 度肯定不会与为量度其坐标而选取的各条轴有关。具体地说,P是一个与坐标系无关的数
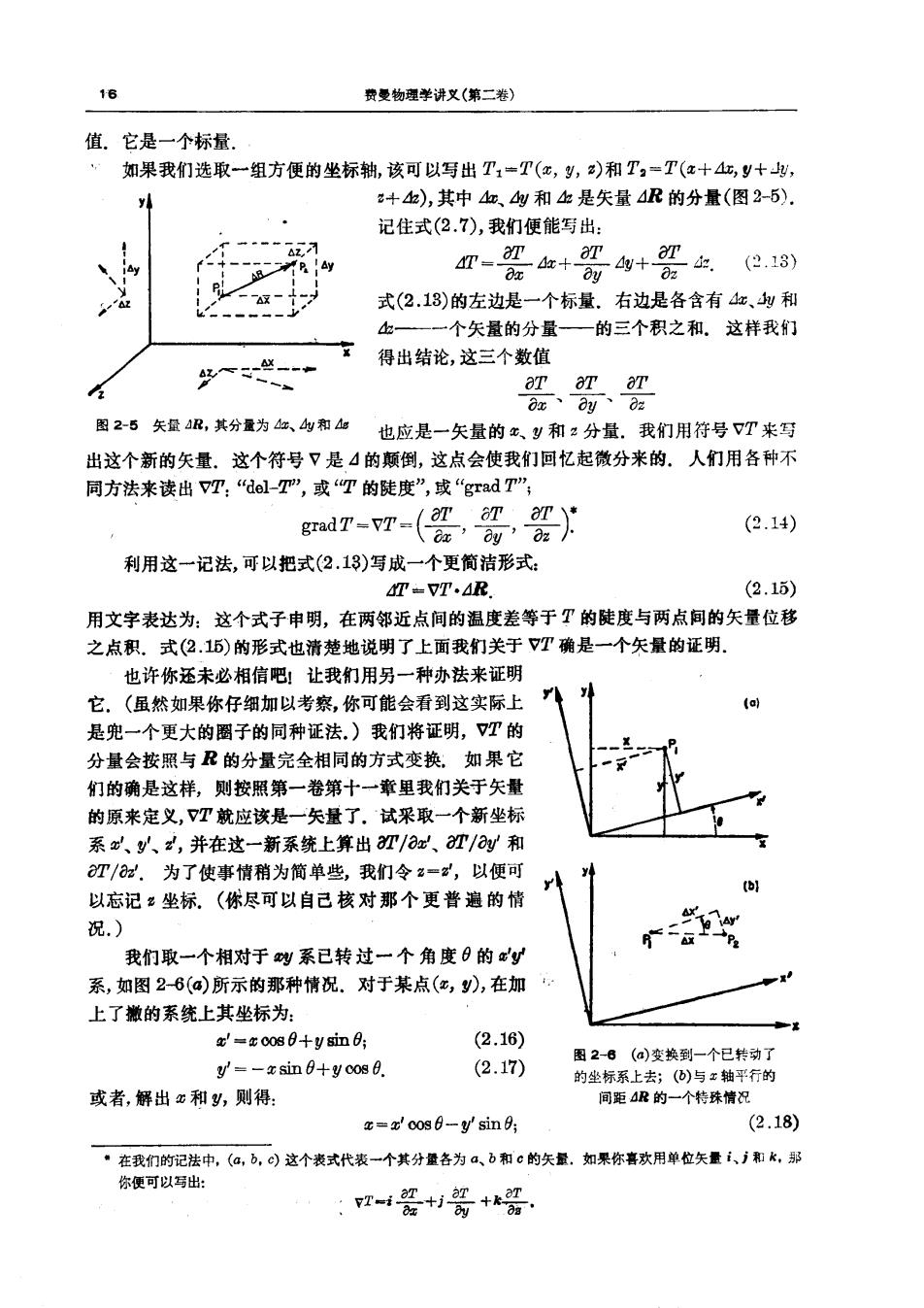
16 费曼物理学讲义(第二卷) 值.它是一个标量, 如果我们选取一组方便的坐标轴,该可以写出T=T(匹,,)和T,=T(z+4血,y+ +),其中红、y和血是矢量4R的分量(图2-5). f----ita 记住式(2.7),我们便能写出: (2.13) 式(2.13)的左边是一个标量.右边是各含有红、y和 一个矢量的分量一 的三个积之和.这样我们 得出结论,这三个数值 图2-5失量B,其分量为、y和恤 也应是一失量的金、和:分量.我们用符号T来写 出这个新的矢量.这个符号7是4的颠倒,这点会使我们回忆起微分来的.人们用各种不 同方法来读出VT:“ol-T”,或T的陡度”,或“grad T”; gradT-T(,av,) (2.14) 利用这一记法,可以把式(2.13)写成一个更简洁形式 T=又T.R (2.15) 用文字表达为:这个式子申明,在两邻近点间的温度差等于T的陡度与两点间的矢量位移 之点积.式(2.15)的形式也清楚地说明了上面我们关于VT确是一个失量的证明. 也许你还未必相信吧!让我们用另一种办法来证明 它 (虽然如果你仔细加以考察,你可能会看到这实际上 兜一个更大的圈子的同种证法)我们将证明,T的 分量会按照与R的分量完全相同的方式变换,如果它 们的确是这样,则按照第一卷第十一章里我们关于矢量 的原来定义,T就应该是一矢量了,试采取一个新坐标 系x、、,并在这一新系统上算出T/x、T/a和 加/以.为了使事情稍为简单些,我们令一云,以便可 (b) 以忘记名坐标.(你尽可以自己核对那个更普避的情 况.) 我们取一个相对于划系已转过一个角度8的' 系,如图26(④)所示的那种情况.对于某点(x,),在加 上了激的系统上其坐标为: x=宝008日十y8n: (2.16) (2.17) 图2-8(@)变换到一个已转动了 y'=-a sin+y cos 0. 的坐标系上去;(®)与x轴平行的 或者,解出x和y,则得 间距4的一个特珠情况 c0s6-y'sin; (2.18) 法中,(@,b,)这个表式代表一个其分量各为a、b和c的矢最.如果你喜欢用单位矢量1、i和k,影 vT-4+i+k第