电子科技大学：《近代天线理论 Modern Antenna Theory》课程教学资源（课件讲稿）07 宽带天线及移动通信天线

近代天线埋论 第四章 宽带天线及移动通信天线 当0→0，R,(0)→0 对(3)进行变换可以得到波特公式 .c)y (4) 定义换能功率增益(Transducer Power Gain) TPG(@)=- =sUof=1-sU®f (5) Sa( Z,(S)-Z,(-) Z(s)+Z(s) (6) 将(1)、(6)带入(5)得到： 4R,(o)R(o) TPG(@)= [R,(o)+R(o)]+[X,(o)+X,(o) (7) 11:51 电子斜枝大学电子工程学院

近代天线理论 第四章 宽带天线及移动通信天线 11:51 电子科技大学电子工程学院 2 2 21 22 ( ) ( ) 1 ( ) in av P S j S j P TPG        22 ( ) ( ) ( ) ( ) ( ) q l s j q l s j Z s Z s S s Z s Z s         2 2 4 ( ) ( ) ( ) [ ( ) ( )] [ ( ) ( )] q l q l q l R R R R X X            TPG dy y y dy dR X q q      0 ln 1 ( ) ( )      对（3）进行变换可以得到波特公式 （4） 定义换能功率增益（Transducer Power Gain) （5） （6） 将（1）、（6）带入（5）得到： （7） 当      , ( ) 0 Rq

近代天线埋论 第四章 宽带天线及移动通信天线 1、用折线逼近待求的R,(o): R,(o)=6+∑a,(o)r °(8) k=1 0k≤0 R(ω） a(0)= 0-00k-1<0<0 0k一0k-i R(w) 9) 0 02 0 0≤0k-1 用折线段逼近一实部函数特性 11:51 电子斜技大学电子工程学院

近代天线理论 第四章 宽带天线及移动通信天线 11:51 电子科技大学电子工程学院 1、用折线逼近待求的 ： 用折线段逼近一实部函数特性 0 1 ( ) ( ) n q k k k R r a r      （8） （9） () Rq ( ) ak  1 1     k k k      k    k1     k  k1 ＝ 1 0

近代天孩埋论 第四章 宽带天线及移动通信天线 应用波特公式求其虚部函数，将(8)代入(4)可得： X(o)=∑b,(@)r (10) k=1 ()lie-)-(-in- (11) -(@x-1+@)In(@i+@)-(@-@-1)In@-@] 11:51 电子斜技大学电子工程学院

近代天线理论 第四章 宽带天线及移动通信天线 11:51 电子科技大学电子工程学院 应用波特公式求其虚部函数，将（8）代入（4）可得 ： 1 ( ) ( ) n k k k X b r      dy y y b k k k k k                1 ln ( ) 1 ( ) 1 1 1 1 1 1 1 ( ) [( )ln( ) ( )ln ( ) ( )ln( ) ( )ln ] k k k k k k k k k k k b                                       （10） （11）

近代天线埋论 第四章 宽带天线及移动通信天线 在频带内取M个频点，并使这些频点对应于实测阻抗数据所 对应的频率，利用最小二乘法，以下式作为目标函数进行优 化，就可以得到对应于最佳TPR(o)的R,(o) F=min 空c,-maor (12) 2、用有理函数Rg(o)逼近折线R,(o): Rg(o)在工程上一般采用 R(0)-j (13) +B,02+.+Bw02w 当网络为低通，k=0;网络为带通，0<k<N;网络为高通， kN。 11:51 电子斜枝大学电子工程骨院

近代天线理论 第四章 宽带天线及移动通信天线 11:51 电子科技大学电子工程学院 在频带内取M个频点，并使这些频点对应于实测阻抗数据所 对应的频率，利用最小二乘法，以下式作为目标函数进行优 化，就可以得到对应于最佳 TPR( )  的 ( ) Rq  2 0 1 min [ ( )] M j F                TPG TPG (12) 2、用有理函数 Rq () 逼近折线 Rq ( )  ： Rq () 2 0 2 2 1 ( ) 1 ... k q N N A R B B         在工程上一般采用 (13) 当网络为低通，k=0；网络为带通， ;网络为高通， k=N。 0 k N

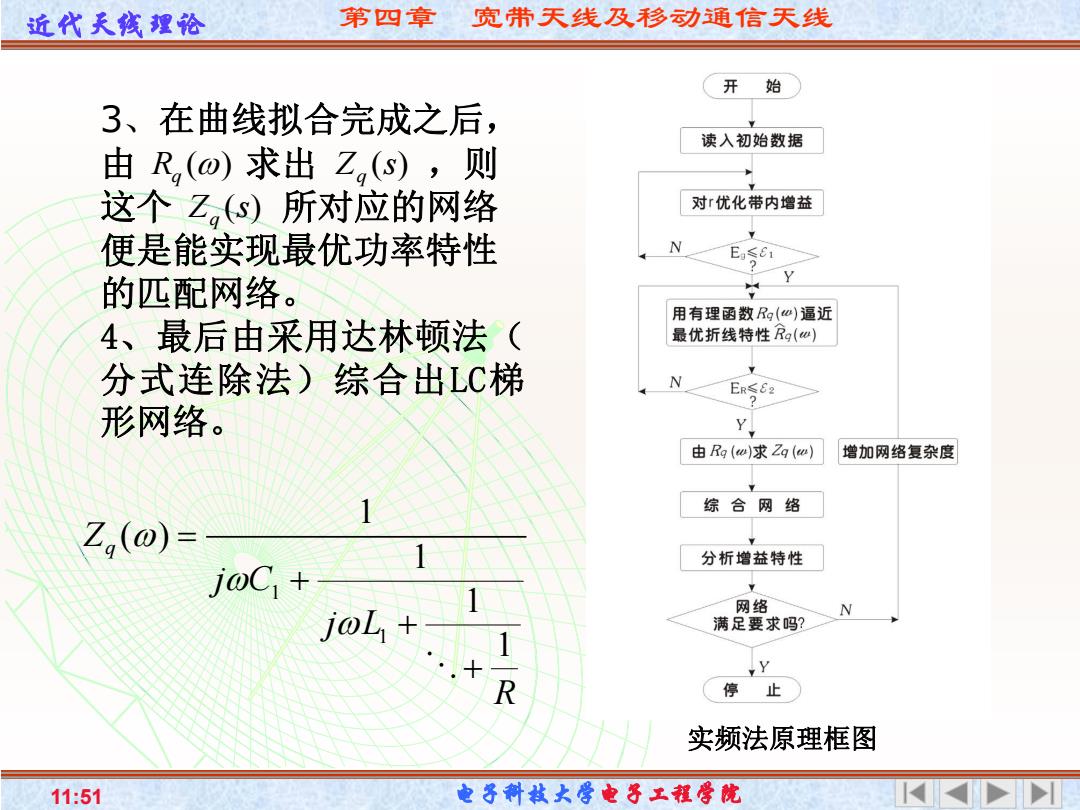
近代天线埋论 第四章 宽带天线及移动通信天线 开始 3、在曲线拟合完成之后， 读入初始数据 由R(o)求出Z,(s),则 这个Z,()所对应的网络 对r优化带内增益 便是能实现最优功率特性 N Eg≤1 的匹配网络。 用有理函数Rg(心)逼近 4、最后由采用达林顿法( 最优折线特性Rg(e) 分式连除法)综合出LC梯 4 ER≤62 形网络。 Y 由Rg(w)求Zg(w) 增加网络复杂度 综合网络 Z(0)= 分析增益特性 j0C1+ 网络 jol 满足要求吗？ R 实频法原理框图 11:51 电子斜枝大学电子工程学院

近代天线理论 第四章 宽带天线及移动通信天线 11:51 电子科技大学电子工程学院 3、在曲线拟合完成之后， 由 求出 ，则 这个 所对应的网络 便是能实现最优功率特性 的匹配网络。 4、最后由采用达林顿法（ 分式连除法）综合出LC梯 形网络。 () Rq Z (s) q Z (s) q 实频法原理框图 1 1 1 ( ) 1 1 1 Zq j C j L R       