
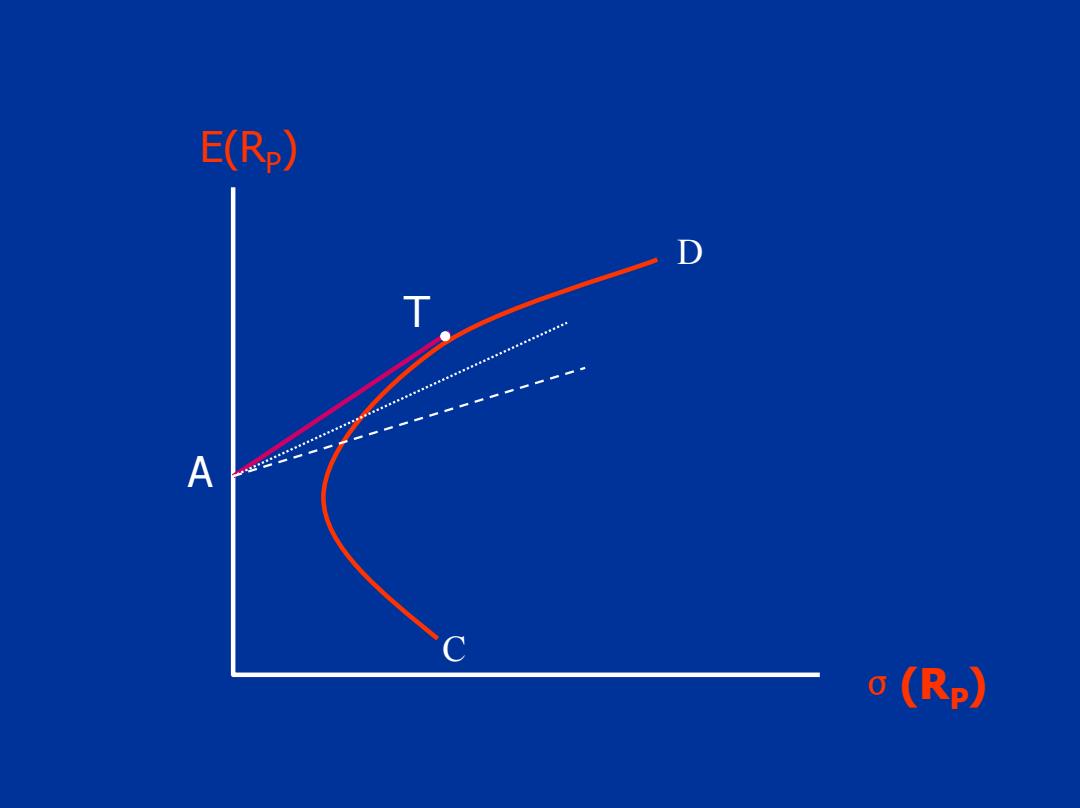
3.无风险贷出对有效集的影响 如前所述,引入无风险贷款后,有效集将 发生重大变化。 图中,弧线CD代表马科维兹有效集,A点 表示无风险资产。我们可以在马科维兹有效集 中找到一点T,使AT直线与弧线CD相切于T点。 T点所代表的组合称为切点处的投资组合
3.无风险贷出对有效集的影响 如前所述,引入无风险贷款后,有效集将 发生重大变化。 图中,弧线CD代表马科维兹有效集,A点 表示无风险资产。我们可以在马科维兹有效集 中找到一点T,使AT直线与弧线CD相切于T点。 T点所代表的组合称为切点处的投资组合

·T点代表马科维兹有效集中众多的有效组合中的一个 但它却是一个很特殊的组合。因为对于所有由风险资 产构成的组合来说,没有哪个点与无风险资产相连接 形成的直线会落在T点与无风险资产的连线的西北方 换句话说,在所有从无风险资产出发到风险资产或是 风险资产组合的连线中,没有哪一条线能比到T点的 线更陡。由于马科维兹有效集的一部分是由这条线所 控制,因而这条线就显得很重要
T点代表马科维兹有效集中众多的有效组合中的一个, 但它却是一个很特殊的组合。因为对于所有由风险资 产构成的组合来说,没有哪个点与无风险资产相连接 形成的直线会落在T点与无风险资产的连线的西北方。 换句话说,在所有从无风险资产出发到风险资产或是 风险资产组合的连线中,没有哪一条线能比到T点的 线更陡。由于马科维兹有效集的一部分是由这条线所 控制,因而这条线 就显得很重要

■从图中可以看出,在引入AT线段之后,即投资者可以投资于 无风险资产时,CT弧将不再是有效集。因为对于T点左边的有 效集而言,在预期收益率相等的情况下,AT线段上风险均小 于马科维兹有效集上的组合的风险,而在风险相同的情况下, AT线段上的预期收益率均大于马科维兹有效集上组合的预期 收益率。按照有效集的定义,CT弧线的有效集将不再是有效 集。由于AT线段上的组合是可行的,因此引入无风险贷款后; 新的有效集由AT线段和TD弧线构成,其中直线段AT代表无风 险资产和T以各种比例结合形成的一些组合
从图中可以看出,在引入AT线段之后,即投资者可以投资于 无风险资产时,CT弧将不再是有效集。因为对于T点左边的有 效集而言,在预期收益率相等的情况下,AT线段上风险均小 于马科维兹有效集上的组合的风险,而在风险相同的情况下, AT线段上的预期收益率均大于马科维兹有效集上组合的预期 收益率。按照有效集的定义,CT弧线的有效集将不再是有效 集。由于AT线段上的组合是可行的,因此引入无风险贷款后, 新的有效集由AT线段和TD弧线构成,其中直线段AT代表无风 险资产和 T 以各种比例结合形成的一些组合
E(Rp) D T A C (Rp)
E(RP) D C T A σ(RP)

4.无风险贷出对投资组合选择的影响 对于不同的投资者而言,无风险贷款的引入对他们的 投资组合选择有不同的影响 对于风险厌恶程度较轻,从而其选择的投资组合位 于DT弧线上的投资者而言,其投资组合的选择将不受影 响。因为只有DT弧线上的组合才能获得最大的满足程度。 对于该投资者而言,他仍将把所有资金投资于风险资产, 而不会把部分资金投资于无风险资产
4.无风险贷出对投资组合选择的影响 对于不同的投资者而言,无风险贷款的引入对他们的 投资组合选择有不同的影响。 对于风险厌恶程度较轻,从而其选择的投资组合位 于DT弧线上的投资者而言,其投资组合的选择将不受影 响。因为只有DT弧线上的组合才能获得最大的满足程度。 对于该投资者而言,他仍将把所有资金投资于风险资产, 而不会把部分资金投资于无风险资产