
7.2.1液体泄漏经管道上的孔洞泄漏一(1)孔洞中流出的液体平均流速为:2g.P(7-4)u=C,va&p定义:新的流出系数Co为:(7-5)C =CiVα孔洞中液体流出速率为:2g.Pgu=CO(7-6)p孔洞面积A已知,则质量流率为:(7-7 )Qm = puA= ACo /2pg.Pg
孔洞中流出的液体平均流速为: gcPg u C 2 = 1 (7-4) 定义: 新的流出系数C0为: 孔洞中液体流出速率为: cPg g u C 2 = 0 (7-6) 孔洞面积A已知,则质量流率为: C0 = C1 (7-5) Qm = uA = AC0 2gcPg (7-7) 7.2.1 液体泄漏——(1) 经管道上的孔洞泄漏

7.2.1液体泄漏一(1)经管道上的孔洞泄漏说明:Co是雷诺数和孔洞直径的复杂函数,为一指导性数据:对锋利的孔洞和Re>30000,Co=0.61,基本上与孔径无关圆滑外形喷嘴,Co=1 ;与容器连接的短管(L/D>3),Co=0.81;C未知时,可取1,释放/泄漏量最大连续操该源模型的适用场合:充满介质的管道作过程的存储容器
说明:C0是雷诺数和孔洞直径的复杂函数,为一指导 性数据: ● 对锋利的孔洞和Re>30000,C0=0.61, 基本上 与孔径无关; ● 圆滑外形喷嘴, C0=1; ● 与容器连接的短管(L/D>3),C0=0.81; ● C0未知时,可取1,释放/泄漏量最大。 该源模型的适用场合:充满介质的管道、连续操 作过程的存储容器 7.2.1 液体泄漏——(1) 经管道上的孔洞泄漏

例 7-1下午1点,工厂的操作人员注意到输送苯的管道中的压力降低了。压力被立即恢复为7atm(表压)。下午2:30,管道中发现了一个直径为0.635cm的小孔并立即进行了修补。请估算流出的苯的总质量。苯的相对密度为878.6kg.m-3.解:A=πd23.165X10-5m2空洞的面积为:4则质量流率为:Qm=ACoV2pg.P.=3.165X10-5X0.61X(2X878.6X1X7X101.325X1000)1/2= 0.682 kg/s则流出的苯的总质量为:Q=0.682X90X60=3683kg
例 7-1 解: 空洞的面积为: • 下午1点,工厂的操作人员注意到输送苯的管道中的压力降低了。压力被立即 恢复为7 atm(表压)。下午2:30,管道中发现了一个直径为0.635 cm的小孔, 并立即进行了修补。请估算流出的苯的总质量。苯的相对密度为878.6kg.m-3 . 则质量流率为: 则流出的苯的总质量为: 3.165×10-5 m2 11 =3.165×10-5×0.61×(2×878.6×1×7×101.325×1000)1/2 = 0.682 kg/s Q= 0.682×90×60=3683 kg
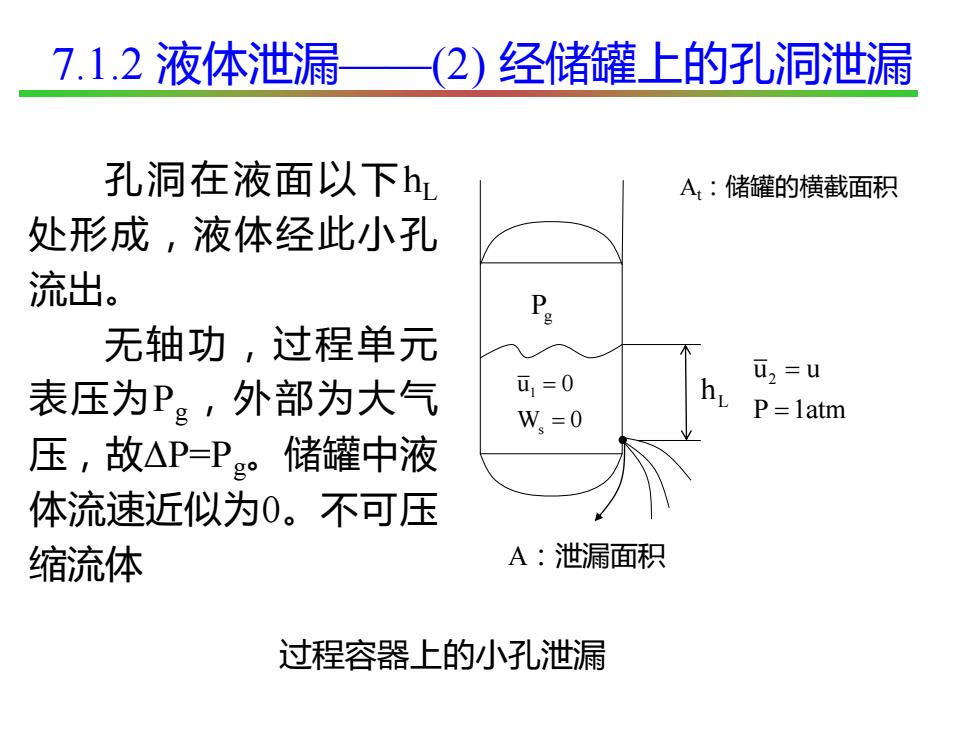
7.1.2液体泄漏(2)经储罐上的孔洞泄漏孔洞在液面以下hrA,:储罐的横截面积处形成,液体经此小孔流出。Po无轴功,过程单元12=uu, =0hy表压为P。,外部为大气P=1atmW.=0压,故△P=P。储罐中液体流速近似为0。不可压A:泄漏面积缩流体过程容器上的小孔泄漏
过程容器上的小孔泄漏 At:储罐的横截面积 A:泄漏面积 1 s u 0 W 0 = = Pg 2 u u P 1atm = = L h 孔洞在液面以下hL 处形成,液体经此小孔 流出。 无轴功,过程单元 表压为Pg,外部为大气 压,故ΔP=Pg。储罐中液 体流速近似为0。不可压 缩流体 7.1.2 液体泄漏——(2) 经储罐上的孔洞泄漏

7.2.1 液体泄漏经储罐上的孔洞泄漏—(2)瞬时(某时刻)释放本源模型可采用机械能守恒:Wdp+8+FS(7-1)m2agcgc无轴功,过程单元表压为P。,外部为大气压,故△P=Pg。储罐中液体流速为0。流出系数G定义为:△P△P60gAZ-H(7-8)7pg.g.P确定孔洞中流出的液体瞬时平均流速为:gclu=CVαgh(7-9)p
瞬时(某时刻)释放 本源模型可采用机械能守恒: (7-8) − − − = − − z g P g z F C g P g c c 2 1 确定孔洞中流出的液体瞬时平均流速为: = + l c g gh g P u C 1 2 (7-9) 流出系数C1定义为: (7-1) m W z F g g ag dP u s c c + + = − + 2 2 无轴功,过程单元表压为Pg,外部为大气压,故ΔP=Pg。储 罐中液体流速为0。 7.2.1 液体泄漏——(2) 经储罐上的孔洞泄漏