第3章受弯构件正截面承载为计算 第三阶段 钢筋塑流阶段,Ⅲa状态:计算Mn的依据 M/M 1.0 M 0.8 内 I a 0.6 0.4 Mer a >5 0 Ⅲa阶段截面应力和应变分布 ◆超过M后,承载力将有所降低,直至压区混凝土压酥。 M称为极限弯矩,此时的受压边缘混凝土的压应变称为极限 压应变u,对应截面受力状态为“Ⅲa状态”。 ◆60.003~0.005,超过该值,压区混凝土开始压坏,梁达 到极限承载力。因此该应变值为计算极限弯矩M的标志。 3.3受弯构件正截面的试验研究
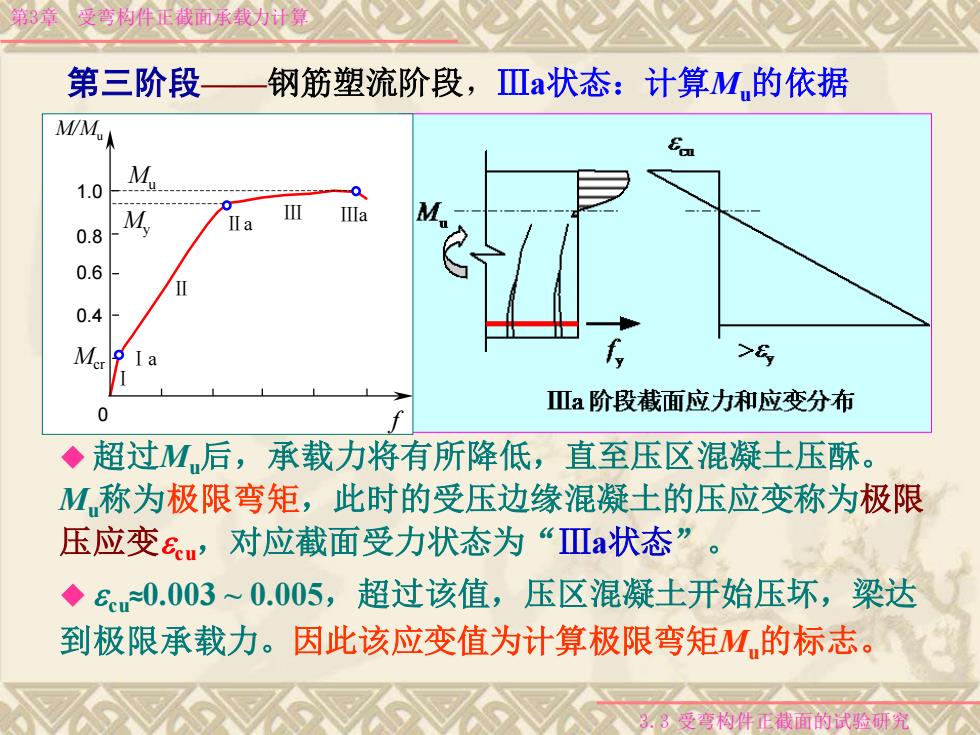
第3章 受弯构件正截面承载力计算 3.3 受弯构件正截面的试验研究 ◆ 超过Mu后,承载力将有所降低,直至压区混凝土压酥。 Mu称为极限弯矩,此时的受压边缘混凝土的压应变称为极限 压应变ecu,对应截面受力状态为“Ⅲa状态”。 ◆ e cu ≈0.003 ~ 0.005,超过该值,压区混凝土开始压坏,梁达 到极限承载力。因此该应变值为计算极限弯矩Mu的标志。 第三阶段——钢筋塑流阶段,Ⅲa状态:计算Mu的依据 0.4 0.6 0.8 1.0 Ⅰa Ⅱa Ⅲa Ⅰ Ⅱ Ⅲ Mcr My Mu 0 f M/Mu
第三阶段 钢筋塑流阶段,Ⅲa状态:计算M的依据 M/M. 1.0 M 0 M a 0.8 0.6 0.4 M a > Ⅲa阶段截面应力和应变分布 配筋合适的钢筋混凝土梁在屈服阶段这种承载力基本 保持不变,变形可以持续很长的现象,表明在完全破坏以 前具有很好的变形能力,有明显的预兆,这种破坏称为 “延性破坏
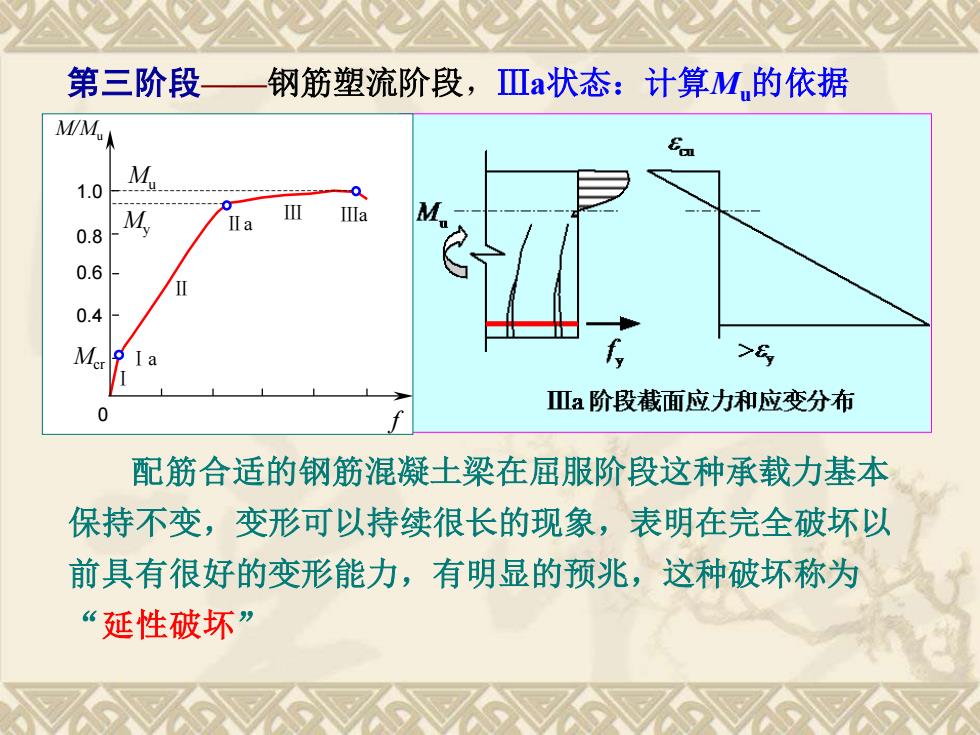
配筋合适的钢筋混凝土梁在屈服阶段这种承载力基本 保持不变,变形可以持续很长的现象,表明在完全破坏以 前具有很好的变形能力,有明显的预兆,这种破坏称为 “延性破坏” 第三阶段——钢筋塑流阶段,Ⅲa状态:计算Mu的依据 0.4 0.6 0.8 1.0 Ⅰa Ⅱa Ⅲa Ⅰ Ⅱ Ⅲ Mcr My Mu 0 f M/Mu

第3章受弯构件正截面承载为计算 T=fA Πa 钢筋混凝土梁三个阶段 .3受弯构件正截面的试验研究
第3章 受弯构件正截面承载力计算 3.3 受弯构件正截面的试验研究
第3竟受弯构件正截而承载力计算 Ia状态:计算Mc的依据 Ⅱ阶段:计算裂缝、刚度的依据 M/M Cu 1.0 Ia状态截面应力和应变分布 M Ⅲa 0.8 0.6 0.4 I a 0 Ⅱ阶段截面应力和应变分布 3.3受弯构件正截面的试验研究
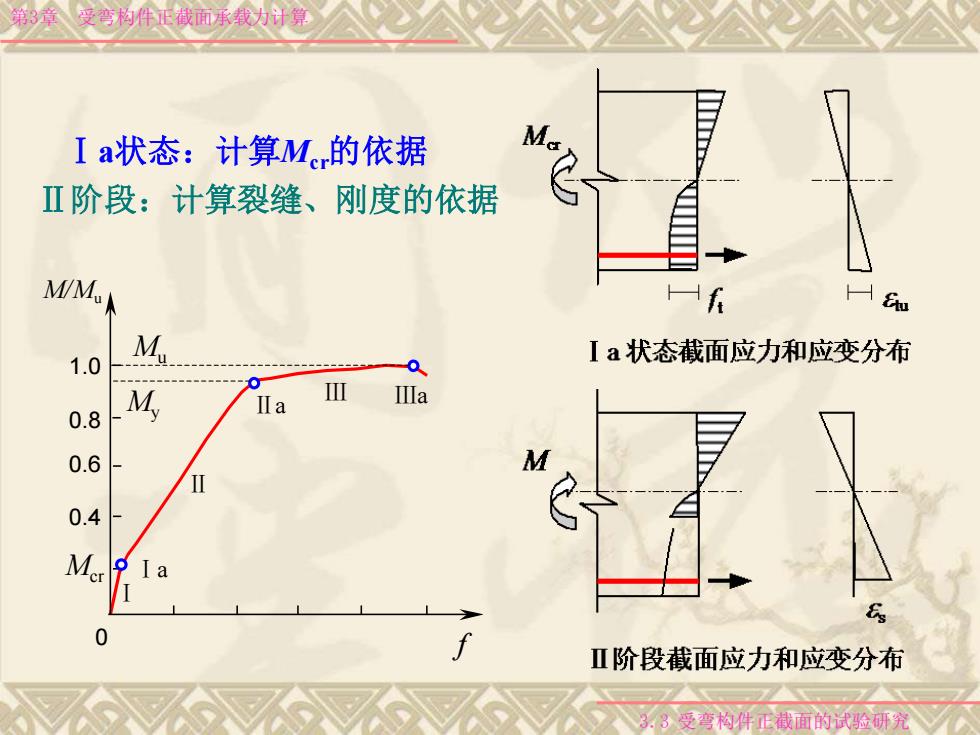
第3章 受弯构件正截面承载力计算 3.3 受弯构件正截面的试验研究 Ⅰa状态:计算Mcr的依据 Ⅱ阶段:计算裂缝、刚度的依据 0.4 0.6 0.8 1.0 Ⅰa Ⅱa Ⅲa Ⅰ Ⅱ Ⅲ Mcr My Mu 0 f M/Mu
第部3章受弯构件正截面承载为计算 M IⅡa状态:计算M,的依据 Ⅲa状态:计算M的依据 MM 04 M Ⅱa状态截面应力和应变分布 1.0 0 0.8 M Ⅱa Ⅲ IIIa 0.6 0.4 >8 0 Ia阶段截面应力和应变分布 33受弯构件正截面的试验研究
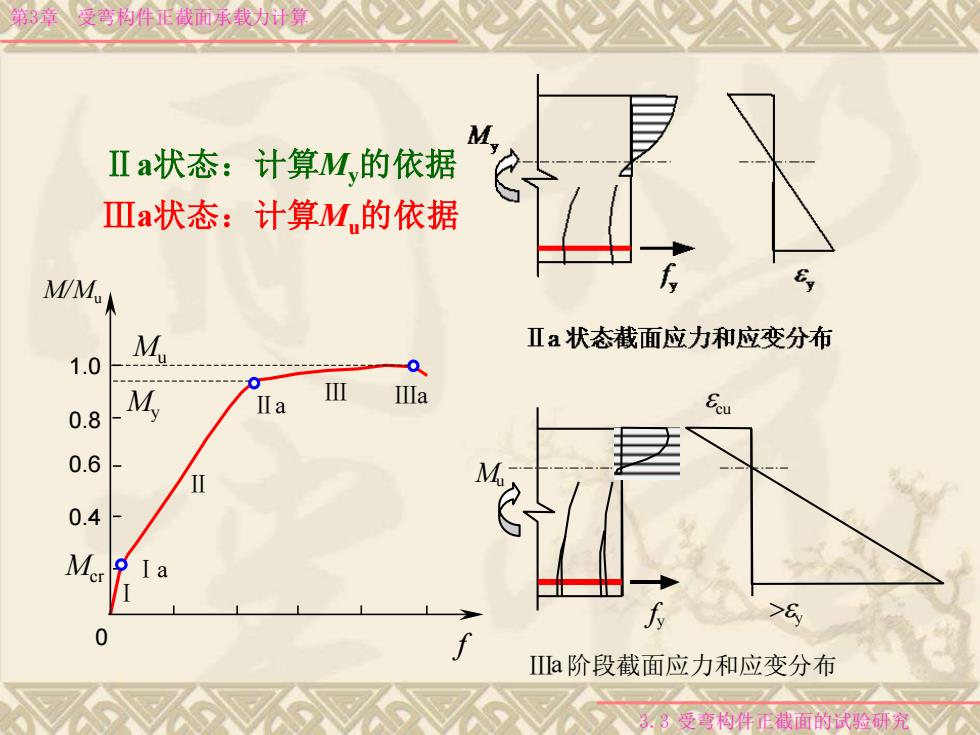
第3章 受弯构件正截面承载力计算 3.3 受弯构件正截面的试验研究 Ⅱa状态:计算My的依据 Ⅲa状态:计算Mu的依据 Mu >ey Ⅲa 阶段截面应力和应变分布 fy ecu 0.4 0.6 0.8 1.0 Ⅰa Ⅱa Ⅲa Ⅰ Ⅱ Ⅲ Mcr My Mu 0 f M/Mu