第竟受弯构件正截面承载力计算 2.弯矩与挠度、曲率、应变及受压区高度的关系 M/M MM 1.0 1.0 0.8 M Ⅲ a 0.8 M 0.6 0 04 I a Per 3.3受弯构件正截面的试验研究
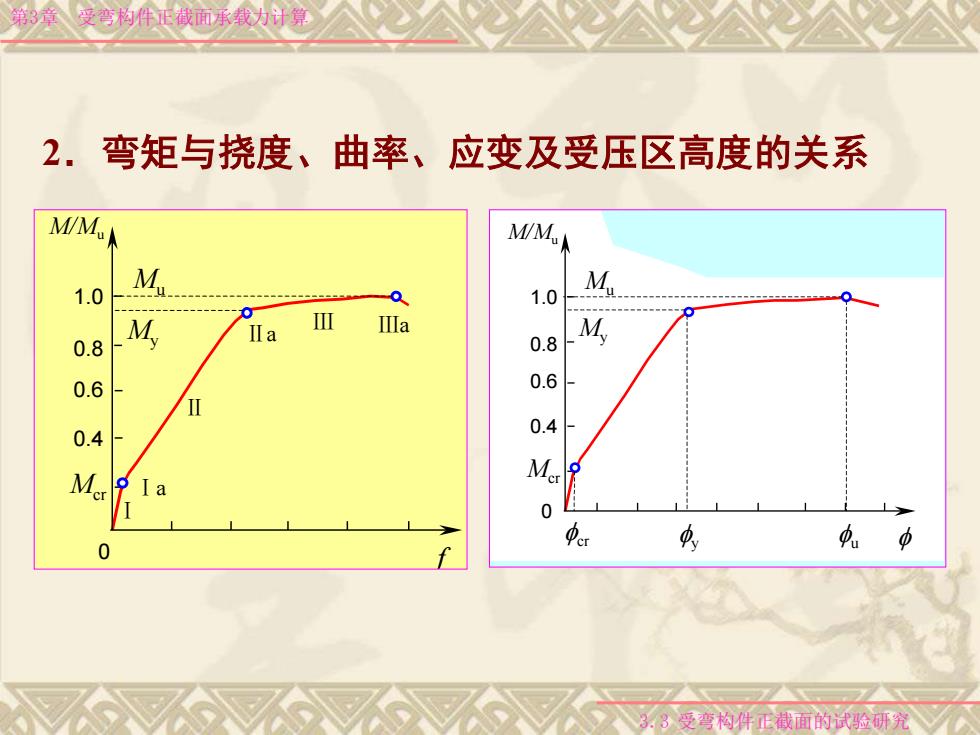
第3章 受弯构件正截面承载力计算 3.3 受弯构件正截面的试验研究 2.弯矩与挠度、曲率、应变及受压区高度的关系 0.4 0.6 0.8 1.0 Ⅰa Ⅱa Ⅲa Ⅰ Ⅱ Ⅲ Mcr My Mu 0 f M/Mu 0.4 0.6 0.8 1.0 Mcr My Mu 0 f M/Mu fcr fy fu
第3章受弯构件正截面承载为计算 2.弯矩与挠度、曲率、应变及受压区高度的关系 M/M M/M M 1.0 0 1.0 II a Ⅲ a 0.8 0.8 M 0.6 0.6 0.4 0.4 a M Sn-x/ho 0 6 00.10.20.30.40.5 3.3受弯构件正截面的试验研究
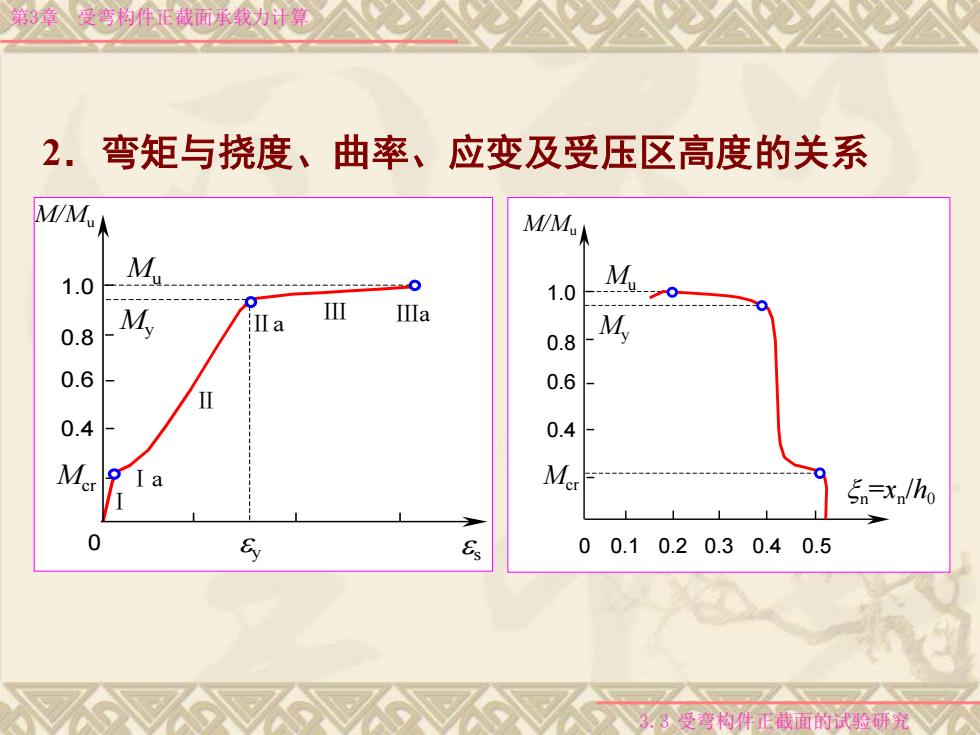
0.4 0.6 0.8 1.0 Ⅰa Ⅱa Ⅲa Ⅰ Ⅱ Ⅲ Mcr My Mu 0 es M/Mu ey 第3章 受弯构件正截面承载力计算 3.3 受弯构件正截面的试验研究 0.4 0.6 0.8 1.0 Mcr My Mu 0 M/Mu 0.1 0.2 0.3 0.4 0.5 x n =xn /h0 2.弯矩与挠度、曲率、应变及受压区高度的关系
第竟受弯构件正截而承载力计算 3.配筋率的影响 钢筋混凝土构件是由钢筋和混凝土两种材料组 成,随着它们的配比变化,将对其受力性能和破坏 形态有很大影响。 配筋率 A bho 3.3受弯构件正截面的试验研究
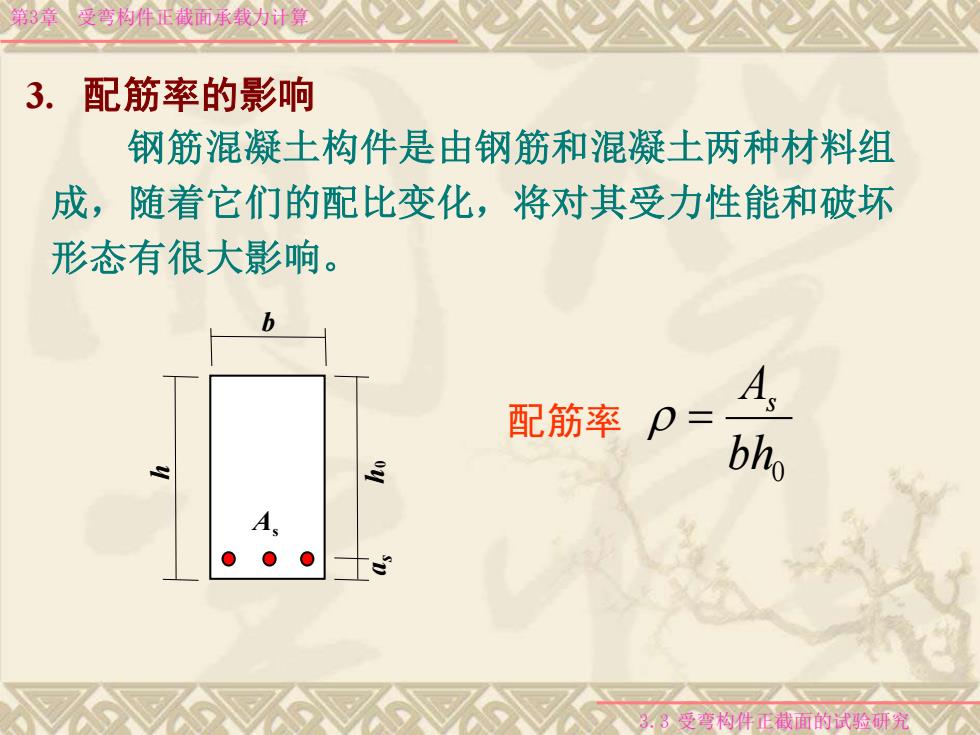
第3章 受弯构件正截面承载力计算 3. 配筋率的影响 钢筋混凝土构件是由钢筋和混凝土两种材料组 成,随着它们的配比变化,将对其受力性能和破坏 形态有很大影响。 配筋率 0 bh As = h 0 h a s As b 3.3 受弯构件正截面的试验研究
第3章受弯构件正截面承载为计算 (1)界限配筋率P MM 配筋率p增大,屈服弯矩 1.0 M增大;屈服时,C增大,xo Ⅲa 0.8 增加,e也相应增大;M→M? 0.6 6一6cu的过程缩短,第阶段 0.4 的变形能力减小。 I a 当p=p时,M,=Ma “a状态”与“a状态”重合。 钢筋屈服与压区混凝土的 M,-M 压坏同时达到,无第Ⅲ阶段, 梁在M,后基本没有变形能力。 界限破坏;界限弯矩M; 界限配筋率p, Ⅱa状态=Ⅲa状态 3:3受弯构件正截面的试验研究
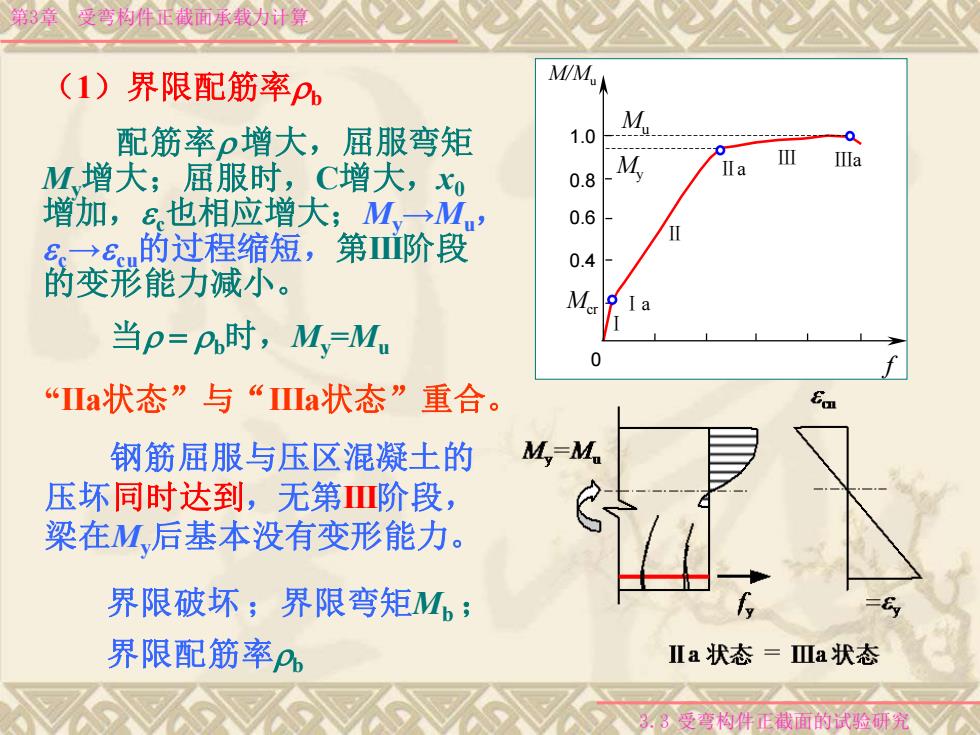
第3章 受弯构件正截面承载力计算 (1)界限配筋率b 配筋率 增大,屈服弯矩 My增大;屈服时,C增大,x0 增加,e c也相应增大;My→Mu, e c→e cu的过程缩短,第III阶段 的变形能力减小。 C xn ec 当 = b时,My =Mu “IIa状态”与“IIIa状态”重合。 钢筋屈服与压区混凝土的 压坏同时达到,无第III阶段, 梁在My后基本没有变形能力。 界限破坏 ;界限弯矩Mb ; 界限配筋率b 3.3 受弯构件正截面的试验研究 0.4 0.6 0.8 1.0 Ⅰa Ⅱa Ⅲa Ⅰ Ⅱ Ⅲ Mcr My Mu 0 f M/Mu
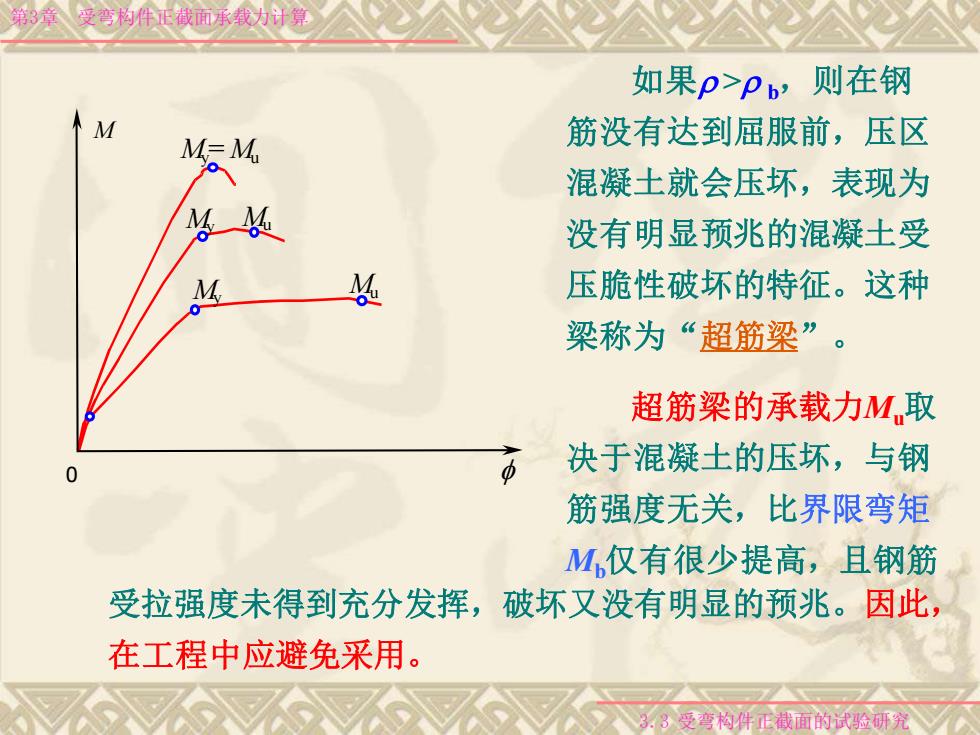
第竟受弯构件正截而承载力计算 如果p>pb,则在钢 MM 筋没有达到屈服前,压区 混凝土就会压坏,表现为 没有明显预兆的混凝土受 压脆性破坏的特征。这种 梁称为“超筋梁”。 超筋梁的承载力M取 决于混凝土的压坏,与钢 筋强度无关,比界限弯矩 M仅有很少提高,且钢筋 受拉强度未得到充分发挥,破坏又没有明显的预兆。因此, 在工程中应避免采用。 3.3受弯构件正截面的试验研究
第3章 受弯构件正截面承载力计算 My Mu 0 f M Mu My My= Mu 如果 > b,则在钢 筋没有达到屈服前,压区 混凝土就会压坏,表现为 没有明显预兆的混凝土受 压脆性破坏的特征。这种 梁称为“超筋梁”。 超筋梁的承载力Mu取 决于混凝土的压坏,与钢 筋强度无关,比界限弯矩 Mb仅有很少提高,且钢筋 受拉强度未得到充分发挥,破坏又没有明显的预兆。因此, 在工程中应避免采用。 3.3 受弯构件正截面的试验研究