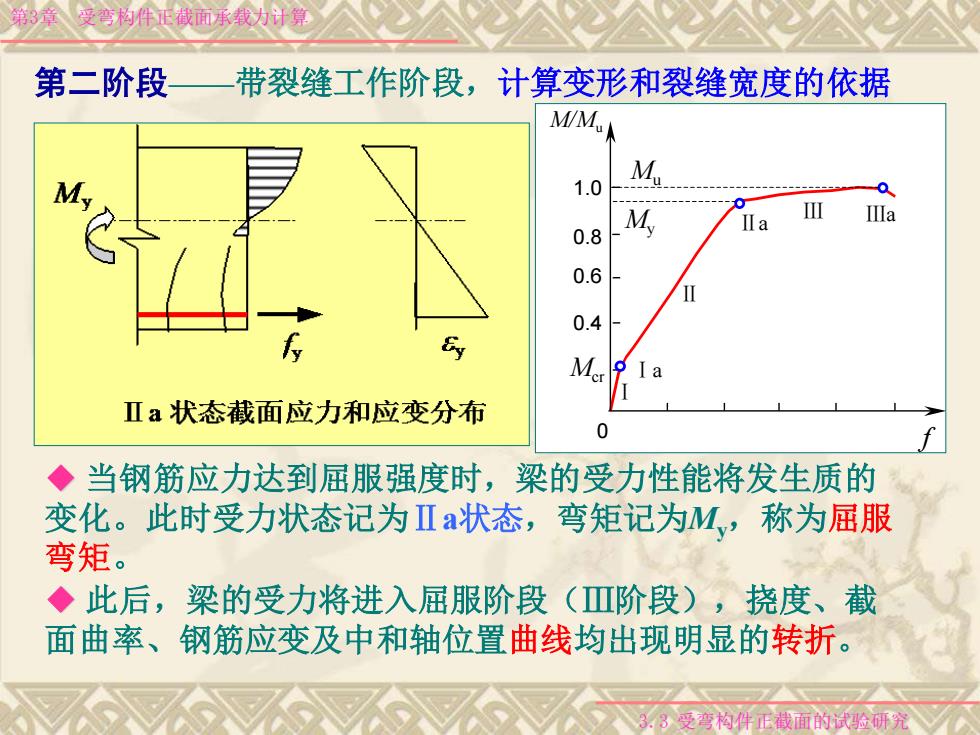
第3章受弯构件正截面承载为计算 第二阶段 带裂缝工作阶段,计算变形和裂缝宽度的依据 M/M.) 1.0 0.8 0.6 0.4 M a Ⅱa状态截面应力和应变分布 ◆当钢筋应力达到屈服强度时, 梁的受力性能将发生质的 变化。此时受力状态记为Ⅱa状态,弯矩记为M,称为屈服 弯矩。 ◆此后,梁的受力将进入屈服阶段(Ⅲ阶段),挠度、截 面曲率、钢筋应变及中和轴位置曲线均出现明显的转折。 3,3受弯构件正截面的试验研究
第3章 受弯构件正截面承载力计算 3.3 受弯构件正截面的试验研究 ◆ 当钢筋应力达到屈服强度时,梁的受力性能将发生质的 变化。此时受力状态记为Ⅱa状态,弯矩记为My,称为屈服 弯矩。 ◆ 此后,梁的受力将进入屈服阶段(Ⅲ阶段),挠度、截 面曲率、钢筋应变及中和轴位置曲线均出现明显的转折。 ◆ 由于受压区混凝土压 应力不断增大,其弹塑 性特性表现得越来越显 著,受压区应力图形逐 渐呈曲线分布。 第二阶段——带裂缝工作阶段,计算变形和裂缝宽度的依据 0.4 0.6 0.8 1.0 Ⅰa Ⅱa Ⅲa Ⅰ Ⅱ Ⅲ Mcr My Mu 0 f M/Mu
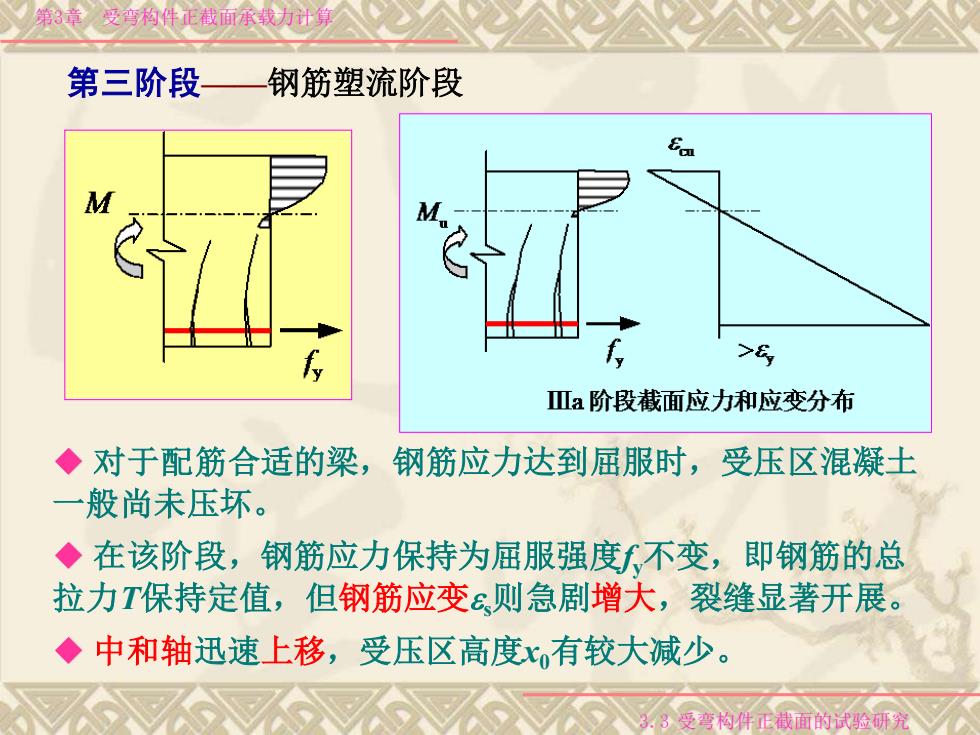
第3章受弯构件正截面承载力计算 第三阶段 —钢筋塑流阶段 >5 Ⅲa阶段截面应力和应变分布 ◆对于配筋合适的梁,钢筋应力达到屈服时,受压区混凝士 一般尚未压坏。 ◆在该阶段,钢筋应力保持为屈服强度不变,即钢筋的总 拉力T保持定值,但钢筋应变ε则急剧增大,裂缝显著开展。 ◆中和轴迅速上移,受压区高度x有较大减少。 .3受弯构件正截面的试验研究
第三阶段——钢筋塑流阶段 第3章 受弯构件正截面承载力计算 ◆ 对于配筋合适的梁,钢筋应力达到屈服时,受压区混凝土 一般尚未压坏。 ◆ 在该阶段,钢筋应力保持为屈服强度fy不变,即钢筋的总 拉力T保持定值,但钢筋应变es则急剧增大,裂缝显著开展。 ◆ 中和轴迅速上移,受压区高度x0有较大减少。 3.3 受弯构件正截面的试验研究
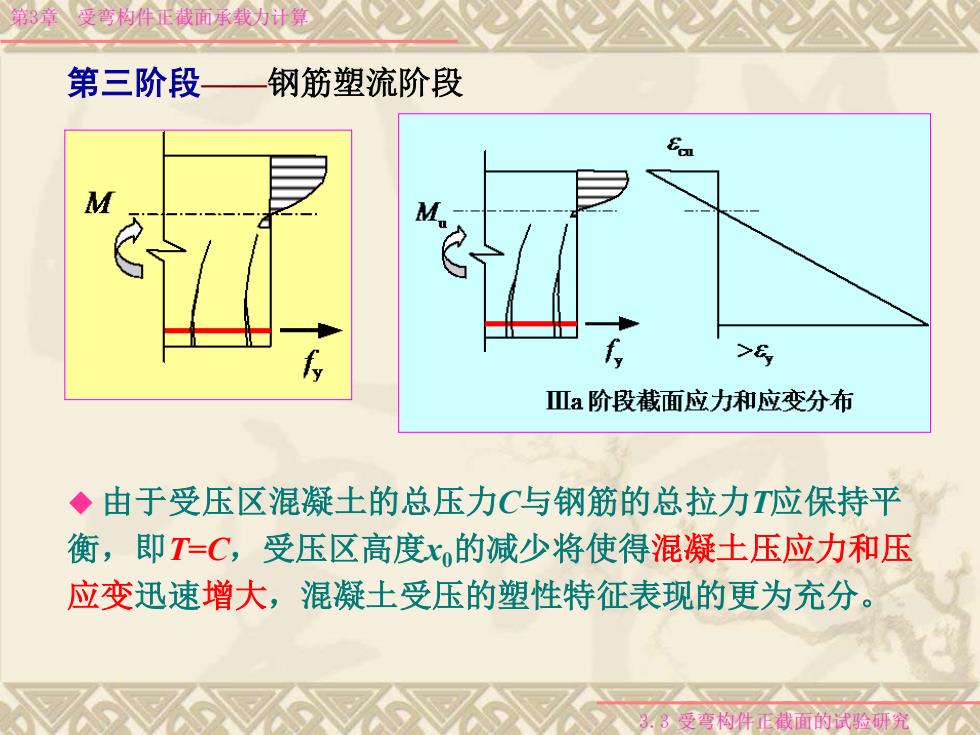
第3章受弯构件正截面承载为计算 第三阶段 钢筋塑流阶段 > Ⅲa阶段截面应力和应变分布 ◆由于受压区混凝土的总压力C与钢筋的总拉力T应保持平 衡,即T=C,受压区高度x的减少将使得混凝土压应力和压 应变迅速增大,混凝土受压的塑性特征表现的更为充分 d 33受弯构件正截面的试验研究
第3章 受弯构件正截面承载力计算 3.3 受弯构件正截面的试验研究 ◆ 由于受压区混凝土的总压力C与钢筋的总拉力T应保持平 衡,即T=C,受压区高度x0的减少将使得混凝土压应力和压 应变迅速增大,混凝土受压的塑性特征表现的更为充分。 第三阶段——钢筋塑流阶段
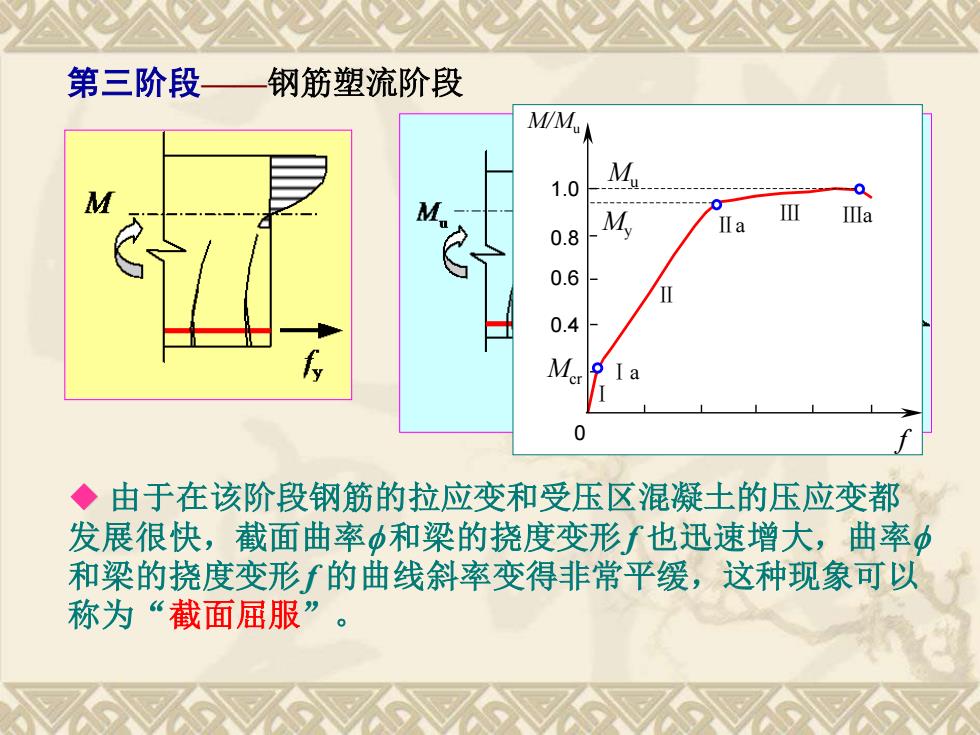
第三阶段 钢筋塑流阶段 M/M 1.0 M M M a 0.8 II a 0.6 0.4 a 0 ◆由于在该阶段钢筋的拉应变和受压区混凝土的压应变都 发展很快,截面曲率和梁的挠度变形f也迅速增大,曲率 和梁的挠度变形f的曲线斜率变得非常平缓,这种现象可以 称为“截面屈服
第三阶段——钢筋塑流阶段 ◆ 由于在该阶段钢筋的拉应变和受压区混凝土的压应变都 发展很快,截面曲率f 和梁的挠度变形f 也迅速增大,曲率f 和梁的挠度变形f 的曲线斜率变得非常平缓,这种现象可以 称为“截面屈服”。 0.4 0.6 0.8 1.0 Ⅰa Ⅱa Ⅲa Ⅰ Ⅱ Ⅲ Mcr My Mu 0 f M/Mu
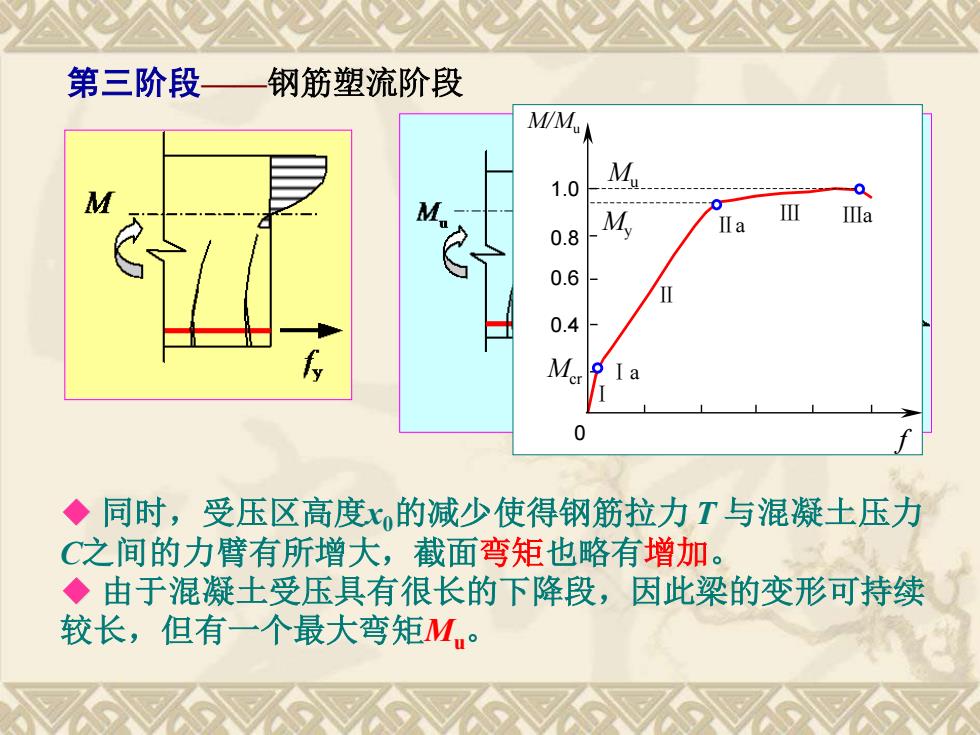
第三阶段 钢筋塑流阶段 M/Mu 1.0 0.8 M Ⅱa Ⅲa 0.6 0.4 a 0 ◆同时,受压区高度x的减少使得钢筋拉力T与混凝土压力 C之间的力臂有所增大,截面弯矩也略有增加。 ◆由于混凝土受压具有很长的下降段,因此梁的变形可持续 较长,但有一个最大弯矩M
◆ 同时,受压区高度x0的减少使得钢筋拉力 T 与混凝土压力 C之间的力臂有所增大,截面弯矩也略有增加。 ◆ 由于混凝土受压具有很长的下降段,因此梁的变形可持续 较长,但有一个最大弯矩Mu。 第三阶段——钢筋塑流阶段 0.4 0.6 0.8 1.0 Ⅰa Ⅱa Ⅲa Ⅰ Ⅱ Ⅲ Mcr My Mu 0 f M/Mu