上海交通大学：《热力系统设计与实践 Design and Practice of Thermodynamic System》课程教学资源（课件讲稿）第09讲 实际气体性质及热力学一般关系式 Behavior of real gases and generalized thermodynamic relationships（压缩因子与范德瓦尔方程等）

第6章 实际气体性质及热力学一做关系式 (Behavior of real gases and generalized thermodynamic relationships) 上游充通大学 2019年3月23日 2 SHANGHAI JLAO TONG UNIVERSIT

2019年3月23日 2 第 6 章 实际气体性质及热力学一般关系式 (Behavior of real gases and generalized thermodynamic relationships)

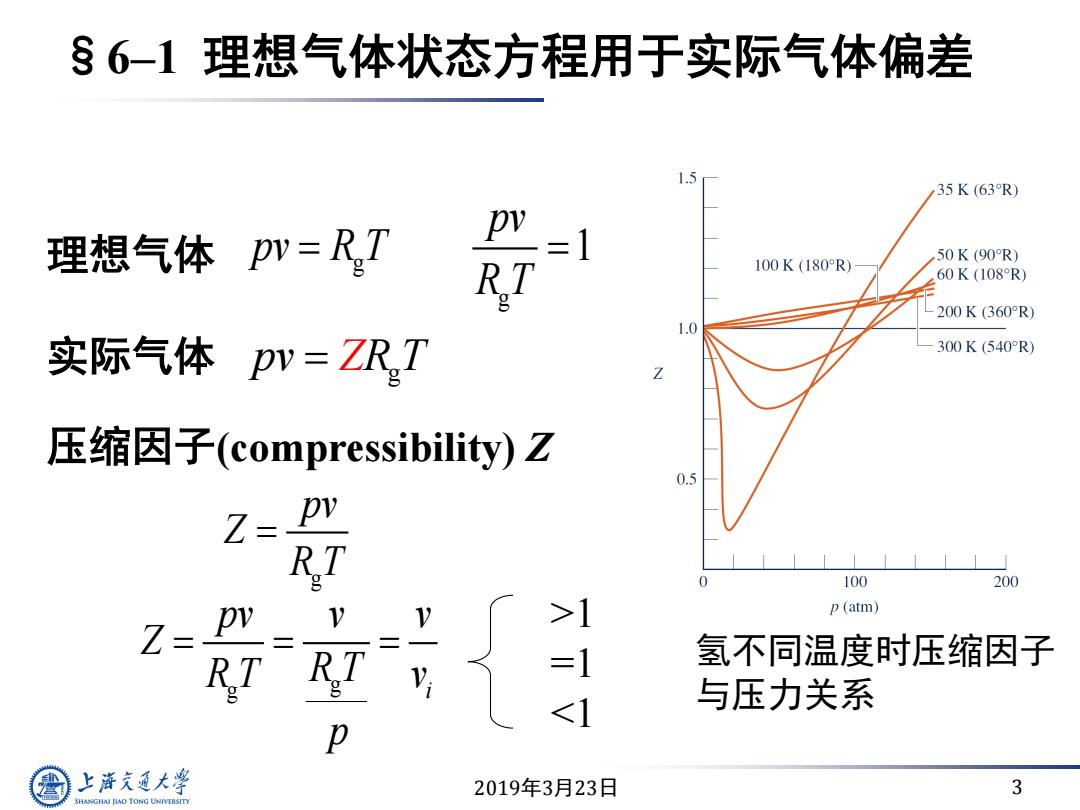
6-1理想气体状态方程用于实际气体偏差 1.5 35K(63R) 理想气体pN=RT =1 50K(90R) R.T 100K(180R) 60K(108R) 200K(360°R) 1.0 实际气体pv=ZRT 300K(540R) 压缩因子(compressibility)Z Z= R 100 200 >1 p (atm) Z 氢不同温度时压缩因子 1 与压力关系 p 上游通大学 2019年3月23日 3 SHANGHAI JLAO TONG UNIVERSITY

2019年3月23日 3 §6–1 理想气体状态方程用于实际气体偏差 理想气体 g g 1 pv pv R T R T   实际气体 g pv T  ZR 压缩因子(compressibility) Z g g i pv v v Z R T v R T p    >1 =1 <1 g pv Z R T  氢不同温度时压缩因子 与压力关系

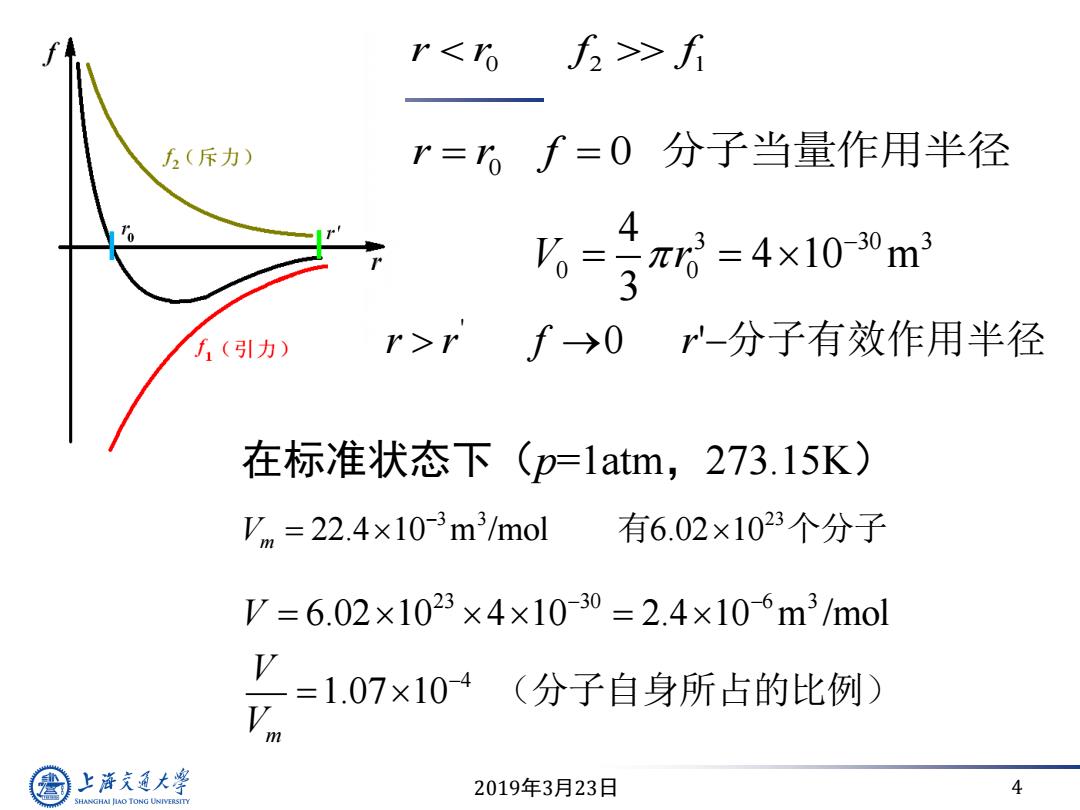
r<r f>>f 方（斥力） r=6f=0分子当量作用半径 4 %=1π=4×100m3 3 方1（引力） r>rf→01 -分子有效作用半径 在标准状态下(p-1atm,273.15K) Vm=22.4×10-3m3/mol 有6.02×1023个分子 V=6.02×1023×4×10-30=2.4×106m3/mol =1.07×10 (分子自身所占的比例) m 上游充通大学 2019年3月23日 4 SHANGHAI JIAO TONG UNIVERSITY

2019年3月23日 4 0 2 1 r r f f   在标准状态下（p=1atm，273.15K） 3 3 23 22.4 10 m /mol 6.02 10 Vm     有 个分子 23 30 6 3 4 6.02 10 4 10 2.4 10 m /mol 1.07 10 m V V V            （分子自身所占的比例） r r f   0 0 分子当量作用半径 3 30 3 0 0 4 4 10 m 3 V r      r  r ' f 0 r'分子有效作用半径

§6-2范德瓦尔方程和R-K方程 一.范德瓦尔方程 (Jahanns Diderik Van der Waals,1873) m-8r一e.小r RT a,b物性常数 或p=V-b a 气态物质较小； 内压力 液态，如水20C时1.05×108Pa (分子引力引起，气体实际施加于壁面的压力比理想气体压力小) (Vmb)一分子自由活动的空间 b-气体体积V中包含气体分子本身的总体积 又称协体积(Covolume) 上游充通大粤 2019年3月23日 5 SHANGHAI JLAO TONG UNIVERSITY

2019年3月23日 5 §6–2 范德瓦尔方程和R-K方程 一.范德瓦尔方程 V b RT V a p m m            2 a, b—物性常数 2 Vm a 内压力 （分子引力引起，气体实际施加于壁面的压力 比 理想气体压力小） 气态物质较小； 液态，如水20℃时1.05×108Pa (Vm–b)—分子自由活动的空间 b – 气体体积V中包含气体分子本身的总体积 又称协体积（Covolume） g pv R T  (Jahanns Diderik Van der Waals, 1873) 2 m m RT a p V b V    或

范氏方程的评价 范氏方程： 1)定性反映气体 p-y-T关系； 范氏方程展开后是体积的立方型方程 2)远离液态时， 即使压力较高，计 算值与实验值误差 C02 323K 较小。如N,常温下 10 350K 100MPa时无显著误 8 304 ed,Ol/d 差。在接近液态时， 误差较大，如C0,常 温下5MPa时误差约 273.16K 4%,100MPa时误差 35%; 0.2 0.4 0.6 3)巨大理论意义 'm/(10-3m3.mol-l ap a >0没有物理意义 上泽充通大 2019年3月23日 6 SHANGHAI JIAO TONG UNIVERSITY

2019年3月23日 6 范氏方程： 1）定性反映气体 p - v - T关系； 2）远离液态时， 即使压力较高，计 算值与实验值误差 较小。如N2常温下 100MPa时无显著误 差。在接近液态时， 误差较大，如CO2常 温下5MPa时误差约 4%，100MPa时误差 35%； 3）巨大理论意义 范氏方程展开后是体积的立方型方程 范氏方程的评价 V b RT V a p m m            2 没有物理意义 𝜕𝑝 𝜕𝑉 𝑇 >0