上海交通大学：《热力系统设计与实践 Design and Practice of Thermodynamic System》课程教学资源（课件讲稿）第10讲 实际气体性质及热力学一般关系式 Behavior of real gases and generalized thermodynamic relationships（对应态原理与通用压缩因子图）

§6-4对应态原理与通用压缩因子图 一，对应态原理(principle of corresponding states) 对比参数(reduced properties):p,=P T,= T T 把对比参数P, T Vw 及 27R2T2 a= b= RT R= .m 64 8Pc 3 T 代入范氏方程： p+ 可导得 是e你 范德瓦尔对比态方程 上游气通大学 2019年3月23日 3 HANGHAI JLAO TONG UNIVERSITY

2019年3月23日 3 §6–4 对应态原理与通用压缩因子图 一.对应态原理(principle of corresponding states) m mr c,m r r c c p T V p T V p T V    代入范氏方程： V b RT V a p m m            2 可导得   m r r m r r V T V p 3 1 8 3 2            范德瓦尔对比态方程 对比参数(reduced properties)： 2 2 27 8 c,m 64 8 3 r r mr c c c c c c p T V R T RT p V a b R p p T    把对比参数 及

n.G 1)sr. 讨论： 1)对比态方程中没有物性常数，所以是通用方程； 2)从对比态方程中可看出 相同的p,T下，不同气体的v不同 相同的p,T下，不同气体的v相同，即 各种气体在对应状态下有相同的比体积 对应态原理f,Ty)=0 3)对大量流体研究表明，对应态原理大致是正确的， 若采用“理想对比体积”一Vm', 能提高计算精度。 m m.i.c 其中Vm.c一临界状态作理想气体计算的摩尔体积 上游充通大学 2019年3月23日 4 HANGHAI JLAO TONG UNIVERSITY

2019年3月23日 4 讨论： 1）对比态方程中没有物性常数，所以是通用方程； 2）从对比态方程中可看出 相同的p，T下，不同气体的v不同 相同的pr，Tr下，不同气体的vr相同，即 各种气体在对应状态下有相同的比体积—— 对应态原理 f(pr ,Tr ,vr )=0 3）对大量流体研究表明，对应态原理大致是正确的， 若采用“理想对比体积”—Vm '，能提高计算精度。 m i c m m V V V , , '  其中 Vm,i,c 临界状态作理想气体计算的摩尔体积   m r r m r r V T V p 3 1 8 3 2           

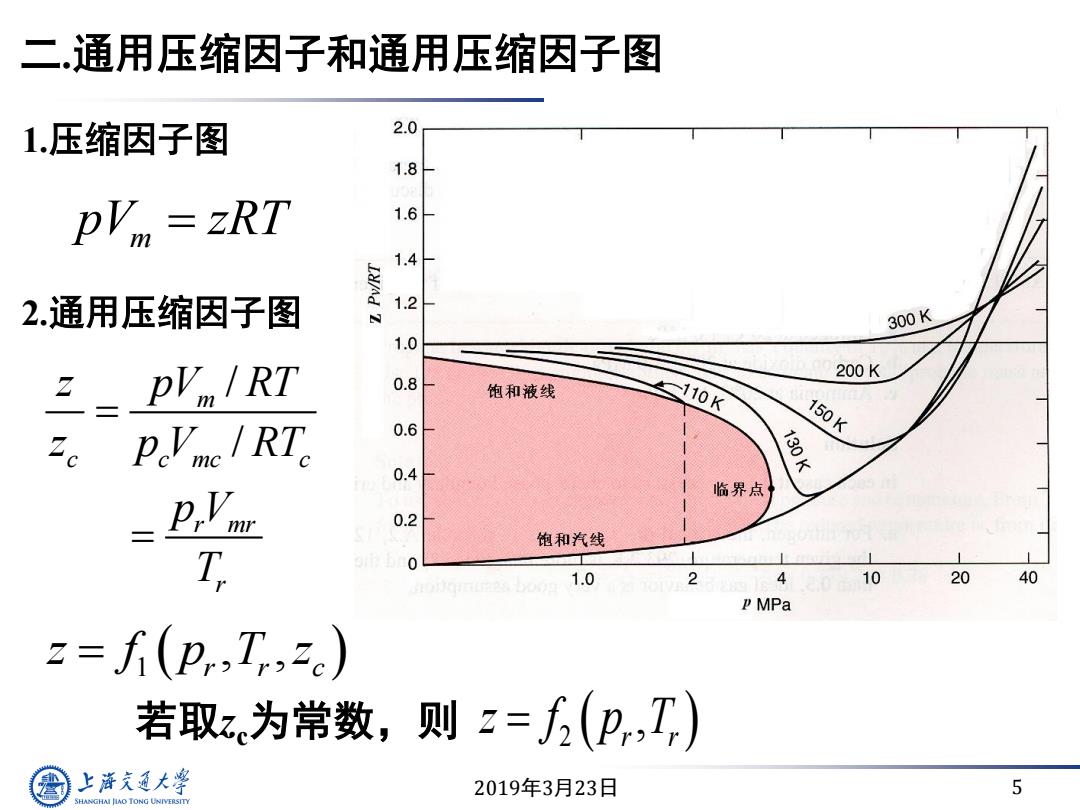
二.通用压缩因子和通用压缩因子图 1.压缩因子图 2.0 1.8 pVn zRT 1.6 1.4- 2.通用压缩因子图 1.2 N 300K 1.0 E=pVn/RT 200K 0.8 饱和液线 110K 0.6 150K Ze PoVmnc/RT 130K 0.4- 临界点 0.2 饱和汽线 T 0 1.0 4 0 10 20 40 P MPa =f(p.T,zc) 若取z为常数，则z=(p,T,) 上游充通大 2019年3月23日 5 SHANGHAI JLAO TONG UNIVERSITY

2019年3月23日 5 二.通用压缩因子和通用压缩因子图 m pV zRT  2.通用压缩因子图 / / m c c mc c r mr r z pV RT z p V RT p V T   若取zc为常数，则   2 , r r z f p T  1.压缩因子图 z f p T z  1  r r c , , 

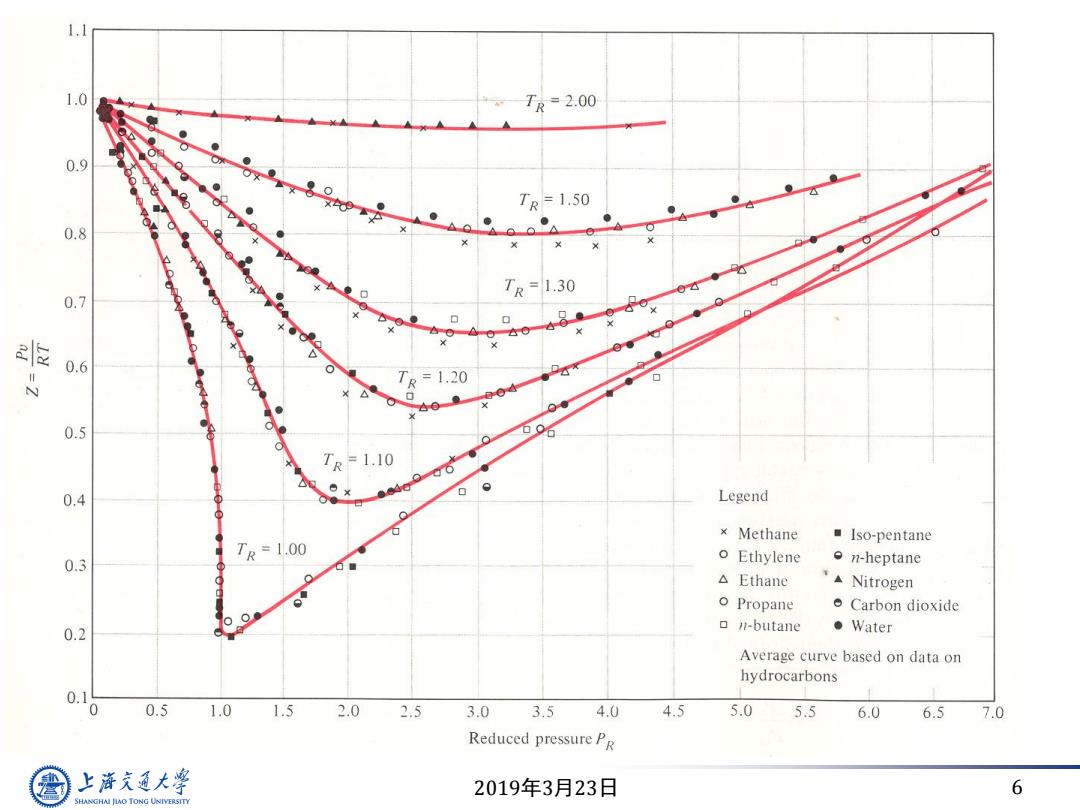
1.0 TR=2.00 0.9 TR=1.50 ● 0.8 TR=1.30 0.7 e 0.6 TR=1.20 ● 0.5 TR=1.10 0.4 Legend × Methane ■lso-pentane Tr=1.00 O 0.3 Ethylene o n-heptane △Ethane Nitrogen o Propane Carbon dioxide 0.2 ▣-butane ● Water Average curve based on data on hydrocarbons 0.1 0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 5.5 6.0 6.5 7.0 Reduced pressure PR 上文通大学 2019年3月23日 6 SHANGHAI JIAO TONG UNIVERSITY

2019年3月23日 6

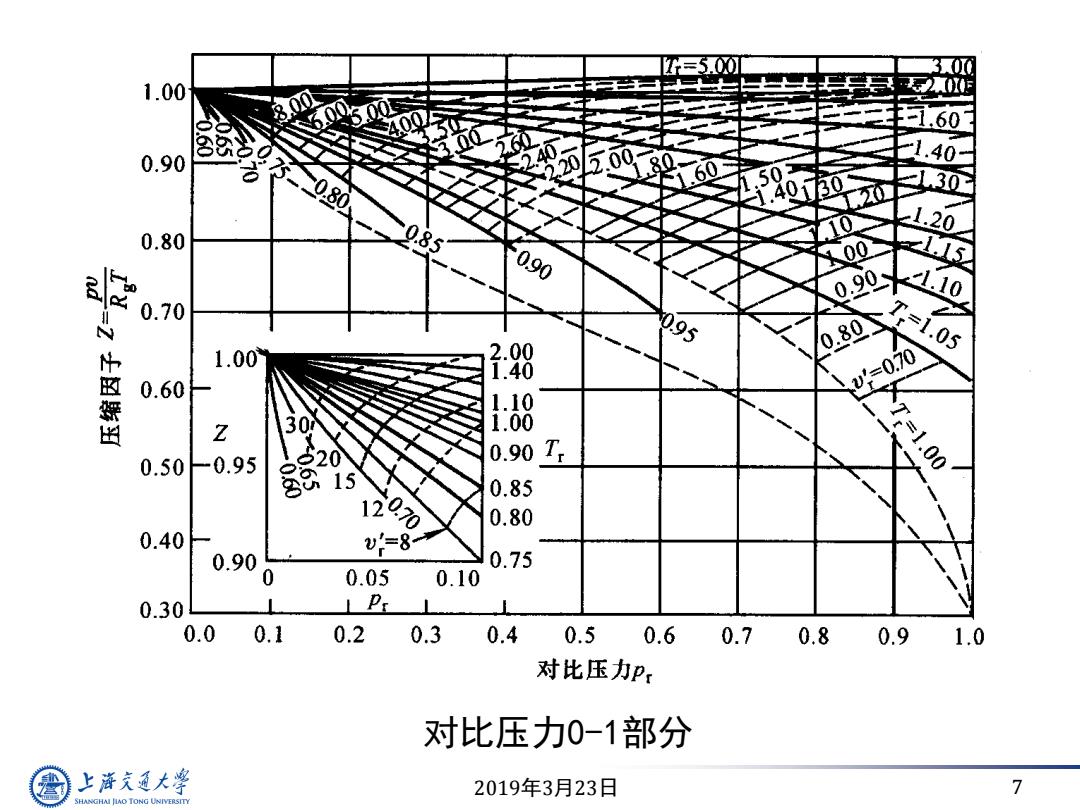
r=300 00 1.00 800 0.90 30 0.80 -0.85 20 090 00 .L5 0.70 0 10 2 0.95 1.05 1.00 0.80 0.60 u070 稻 Z 0.95 0.90T 0.50 =1.00 3 15 20% 0.85 0.80 0.40 v=8 0.90 0.75 0 0.05 0.10 0.30 IPr 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.91.0 对比压力pr 对比压力0-1部分 上游究通大学 2019年3月23日 7 SHANGHAI JLAO TONG UNIVERSITY

2019 年 3 月23 日 7 对比压力 0 - 1部分