
桥梁计算的一般规定 3)车轮在板的支承处时 a=(a1+2h)+t (4.1.3-4) 4)车轮在板的支承附近,距支点的距离为x时 a=(a1+2h)+t+2x (4.1.3-5) 但不大于车轮在板的跨径中部的分布宽度; 5)按本条算得的所有分布宽度,均不得大于板的全宽度; 6)彼此不相连的预制板,车轮在板内分布宽度不得大于预制板宽度。 式中一板的计算跨径; h- 铺装层厚度; t 一板的厚度; d一多个车轮时外轮之间的中距; 41、b1一一垂直于板跨和平行于板跨方向的车轮着地尺寸。 4.1.4当整体式斜板桥的斜交角(板的支承轴线的垂直线与桥纵轴线的夹角)不大于 15时,可按正交板计算,计算跨径为:当l/b≤1.3时,按两支承轴线间垂直距离的正跨径 计算;当/b>1.3时,按顺桥向纵轴线的斜跨径计算;以上1为斜跨径,b为垂直于桥纵 轴线的板宽。 装配式铰接斜板桥的预制板块,可按宽为两板边垂直距离,计算跨径为斜跨径的正交 板计算。 4.1.5垂直于悬臂板跨径方向的车轮荷载分布宽度,当c值(图4.1.5)不大于2.5m 时,可按下列公式计算: a=(a1+2h)+2c (4.1.5) 式中 垂直于悬臂板跨径的车轮荷载分布宽度; aj- -垂直于悬臂板跨径的车轮着地尺寸; 平行于悬臂板跨径的车轮着地尺寸的外缘,通过铺装层45°分布线的外边线 至腹板外边缘的距离; h 铺装层厚度。 4.1.6与梁肋整体连接且具有承托的板(图4.1.6),当进行承托内或肋内板的截面验 算时,板的计算高度可按下式计算: h。=hf+s'tana (4.1.6) 式中h。 一自承托起点至肋中心线之间板的任一验算截面的计算高度; (—不计承托时板的厚度; -自承托起点至肋中心线之间的任一验算截面的水平距离: -承托下缘与悬臂板底面夹角,当tana大于1/3时,取1/3。 15

公路铜筋混凝土及预应力混凝土桥涵设计规范(心D62一2004) 图4.1.5车轮荷载在悬臂板上的分布 图4.1.6承托处板的计算高度 1-桥面装:2-腹板:3悬臂板 4.2梁的计算 4.2.1结构的作用(或荷载)效应可按弹性理论进行计算。对超静定结构,在进行作用 (荷载)效应分析时,结构构件的抗弯刚度可采用:允许开裂的构件0.8E1,不允许开裂的 构件E。I;其中1为混凝土毛截面惯性矩。 4.2.2T形截面梁的翼缘有效宽度br',应按下列规定采用 1内梁的翼缘有效宽度取下列三者中的最小值: 1)对于简支梁,取计算跨径的1/3。对于连续梁,各中间跨正弯矩区段,取该计算 跨径的0.2倍:边跨正弯矩区段,取该跨计算跨径的0.27倍;各中间支点负弯矩 区段,取该支点相邻两计算跨径之和的0.07倍: 2)相邻两梁的平均间距; 3)(b+2b+12h),此处,b为梁腹板宽度,b为承托长度,h为受压区翼缘悬出 板的厚度。当h/bh<1/3时,上式b,应以3hh代替,此处h为承托根部厚度。 2外梁翼缘的有效宽度取相邻内梁翼缘有效宽度的一半,加上腹板宽度的1/2,再 加上外侧悬臂板平均厚度的6倍或外侧悬臂板实际宽度两者中的较小者。 预应力混凝土梁在计算预加力引起的混凝土应力时,预加力作为轴向力产生的应力可 按实际翼缘全宽计算;由预加力偏心引起的弯矩产生的应力可按翼缘有效宽度计算。 对超静定结构进行作用(或荷载)效应分析时,T形截面梁的翼缘宽度可取实际全宽。 4.2.3箱形截面梁在腹板两侧上、下翼缘的有效宽度b可按下列规定计算(图4.2.3 1、图4.2.3-2和表4.2.3): 1 简支梁和连续梁各跨中部梁段,悬臂梁中间跨的中部梁段 bmi =prbi (4.2.31) 2简支梁支点,连续梁边支点及中间支点,悬臂梁悬臂段 bmi=p,bi (4.2.3-2) 式中 bm一腹板两侧上、下各翼缘的有效宽度,i=1,2,3,…见图4.2.3-1; bi -腹板两侧上、下各翼缘的实际宽度,i=1,2,3,…见图4.2.31; —16
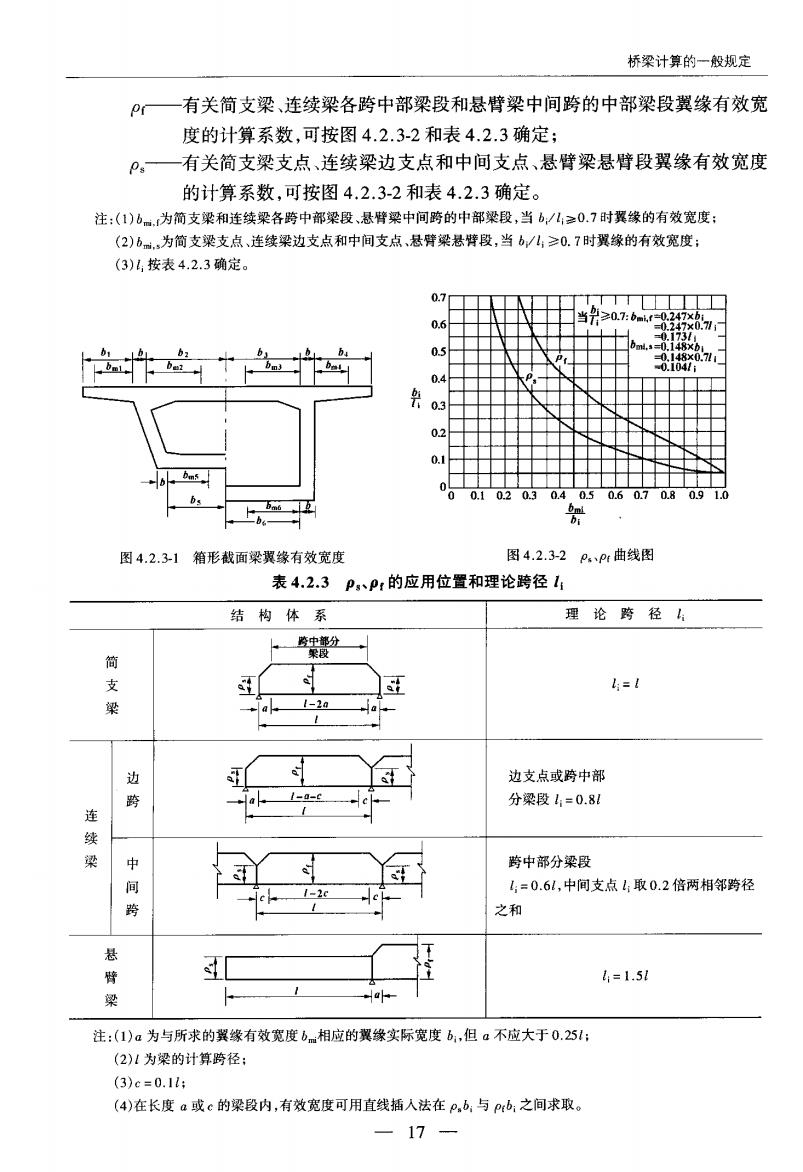
桥梁计算的一般规定 一有关简支梁、连续梁各跨中部梁段和悬臂梁中间跨的中部梁段翼缘有效宽 度的计算系数,可按图4.2.3-2和表4.2.3确定; P. 一有关简支粱支点、连续梁边支点和中间支点、悬臂梁悬臂段翼缘有效宽度 的计算系数,可按图4.2.3-2和表4.2.3确定。 注:(1)b。为简支梁和连续梁各跨中部梁段,悬臂梁中间骑的中部梁段,当b儿,≥0.7时翼缘的有效宽度: (2)6。为简支梁支点、连续梁边支点和中问支点、悬臂梁悬特段,当6/儿,≥0.7时翼缘的有效宽度: (3)儿,按表4.23确定。 0.6 0.1483 上 图4.2.31箱形截面梁翼缘有效宽度 图4.2.3-2A,P曲线图 表4.2.3pP:的应用位置和理论跨径1 结构体系 理论跨径 支 k=1 梁 a a 边 边支点或跨中部 =a-fc 分梁段1=0.81 连 跨中部分梁段 间 ,=0.6l,中间支点1取0.2倍两相邻骑径 之和 起 4=1.51 注:(1)a为与所求的翼缘有效宽度bm相应的翼缘实际宽度b,但a不应大于0,25: (2)1为梁的计算畸径: (3)c=0.1h: (4)在长度a或c的梁段内,有效宽度可用直线括人法在P,.d,与prb:之间求取。 -17

公路钢筋混凝土及预应力混凝土桥涵设计规范(J心D62一2004) 当梁高h≥b/0.3时,翼缘有效宽度应采用翼缘实际宽度。 预应力混凝土梁在计算预加力引起的混凝土应力时,预加力作为轴向力产生的应力 可按实际翼缘全宽计算;由预加力偏心引起的弯矩产生的应力可按翼缘有效宽度计算。 对超静定结构进行作用(或荷载)效应分析时,箱形截面梁的翼缘宽度可取实际全宽。 4.2.4计算连续梁中间支承处的负弯矩时,可考虑支座宽度对弯矩折减的影响:折减 后的弯矩按下列公式计算(图4.2.4):但折减后的弯矩不得小于未经折减的弯矩的0.9 倍c M。=M-M (4.2.4-1) M=8q02 (4.2.4-2) 式中M。一折减后的支点负弯矩; M- 按理论公式或方法计算的支点负弯矩: M'- 折减弯矩: 梁的支点反力R在支座两侧向上按45分布于梁截面重心轴GG的荷载强 度,g=R/a; 梁支点反力在支座两侧向上按45°扩散交于重心轴GG的长度(圆形支座 可换算为边长等于0.8倍直径的方形支座)。 图4.2.4中间支承处折减弯矩计算图 4.2.5设有承托的连续梁,其承托竖向与纵向之比不宜大于1/6。变高度或等高度但 支点设有承托的连续梁,计算作用(或荷载)效应时应考虑截面惯性矩的变化:但当支点截 面惯性矩与跨径中点截面惯性矩之比等于或小于2时,可不考虑其截面惯性矩变化的影 响。 4.2.6当连续梁中间支承处设有横隔梁时,支座上的计算截面可采用横隔梁侧面的连 续梁截面。 4.2.7计算变高度梁(包括等高度梁设有承托的梁段)的剪应力时,应考虑弯矩、轴向 力引起的附加剪应力。 18

桥梁计算的一般规定 4.2.8计算连续梁或其他超静定结构的作用(或荷载)效应时,应根据情况考虑温度 混凝土收缩和徐变、基础不均匀沉降等作用影响。对于预应力混凝土连续梁等超静定结 构,还应考虑预加力引起的次效应。 4.2.9计算混凝土徐变时,可假定徐变与混凝土应力呈线性关系。当缺乏符合当地实 际条件的数据和计算方法时,混凝土徐变系数,可按本规范表6.2.7采用或按附录F计 算。 混凝土的收缩应变可按本规范表6.2.7采用或按附录F计算。 4.2.10由于日照正温差和降温反温差引起的梁截面应力,可按附录B计算。竖向日 照温差梯度曲线可按《公路桥涵设计通用规范》(JTGD60一2004)取用。 4.2.11若预应力混凝土连续梁在施工过程中不转换结构体系,在混凝土徐变完成后, 由预加力引起的总的次效应(包括弹性变形和徐变),可由预加应力时引起的弹性变形次 效应乘以预应力钢筋张拉力的平均有效系数C求得。平均有效系数按下式计算: C=P/P (4.2.11 式中P。—预应力损失全部完成后,预应力钢筋平均张拉力; P 一预应力瞬时(第一批)损失完成后,预应力钢筋平均张拉力。 4.2.12若连续梁在施工过程中转换结构体系(如先期结构在τo时同时加载的简支梁 或其他结构体系,在π时同时转换为后期结构的连续梁),由于混凝土徐变影响,后期结 构上弯矩可按下列规定计算: 】在先期结构上由于结构自重产生的弯矩,经过混凝土徐变重分配,在后期结构中 t时的弯矩M,可按下式计算: Mg=M1g+(M2g-Me)l-e-[.-,5川小 (4.2.12-1) 式中Mg 一在先期结构自重作用下,按先期结构体系计算的弯矩; M2g一在先期结构自重作用下,按后期结构体系计算的弯矩; (t,to)- -从先期结构加载龄期τo至后期结构计算所考虑时间:时的徐变系数,当 缺乏符合当地实际条件的数据时,可按本规范附录F计算; (,0)- 一从先期结构加载龄期o至t时转换为后期结构的徐变系数。 2在先期结构上由预加力产生的弯矩,经过混凝土徐变重分配,在后期结构中,时 的弯矩M,可按下式计算: Mn=Me+(M-MD1-e-)-]月 (4.2.12-2) MiptMipt Mim (4.2.12-3) 式中M1m一在先期结构中的预加力作用下,按先期结构体系计算的弯矩; 19