
Chapter 2 Bearing capacity of foundation 承载力) In lesson of soil mechanics,we've learned Allowable bearing capacity of shallow foundations based on depth of plastic zone(从塑性区的深度计算浅基础地基 容许承载力) Design value of bearing capacity(地基承 载力的设计值)
Chapter 2 Bearing capacity of foundation (基础 承载力) In lesson of soil mechanics, we’ve learned ▪ Allowable bearing capacity of shallow foundations based on depth of plastic zone (从塑性区的深度计算浅基础地基 容许承载力) ▪ Design value of bearing capacity (地基承 载力的设计值)
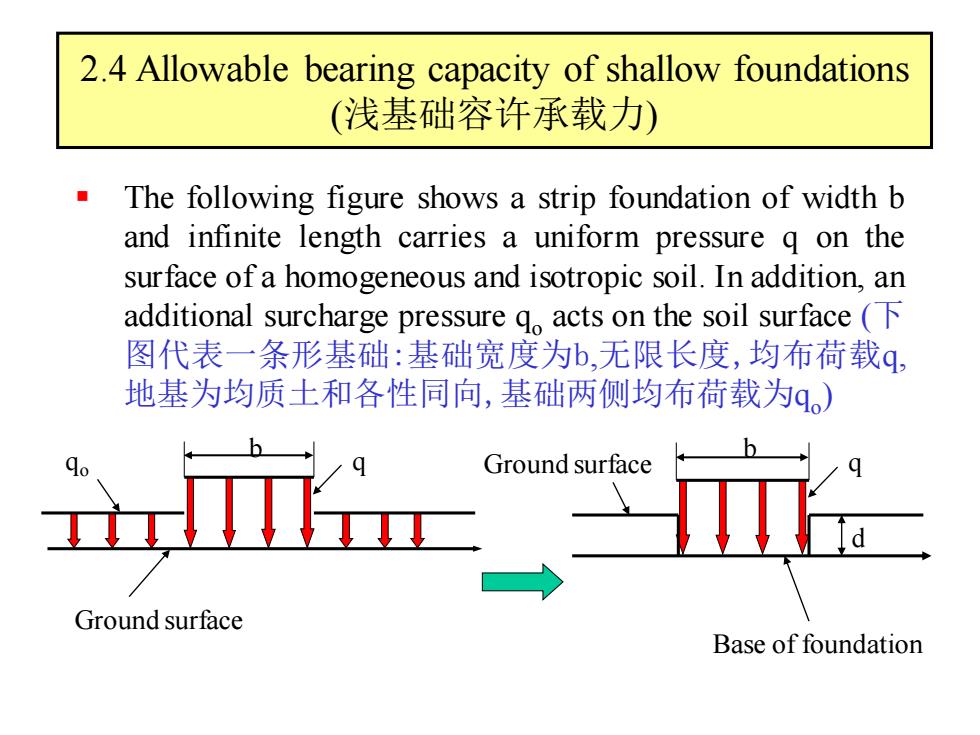
2.4 Allowable bearing capacity of shallow foundations (浅基础容许承载力) The following figure shows a strip foundation of width b and infinite length carries a uniform pressure q on the surface of a homogeneous and isotropic soil.In addition,an additional surcharge pressure qo acts on the soil surface 图代表一条形基础:基础宽度为b,无限长度,均布荷载q, 地基为均质土和各性同向,基础两侧均布荷载为q。) Ground surface Ground surface Base of foundation
2.4 Allowable bearing capacity of shallow foundations (浅基础容许承载力) ▪ The following figure shows a strip foundation of width b and infinite length carries a uniform pressure q on the surface of a homogeneous and isotropic soil. In addition, an additional surcharge pressure qo acts on the soil surface (下 图代表一条形基础:基础宽度为b,无限长度,均布荷载q, 地基为均质土和各性同向,基础两侧均布荷载为qo ) Ground surface q b qo Ground surface q b d Base of foundation
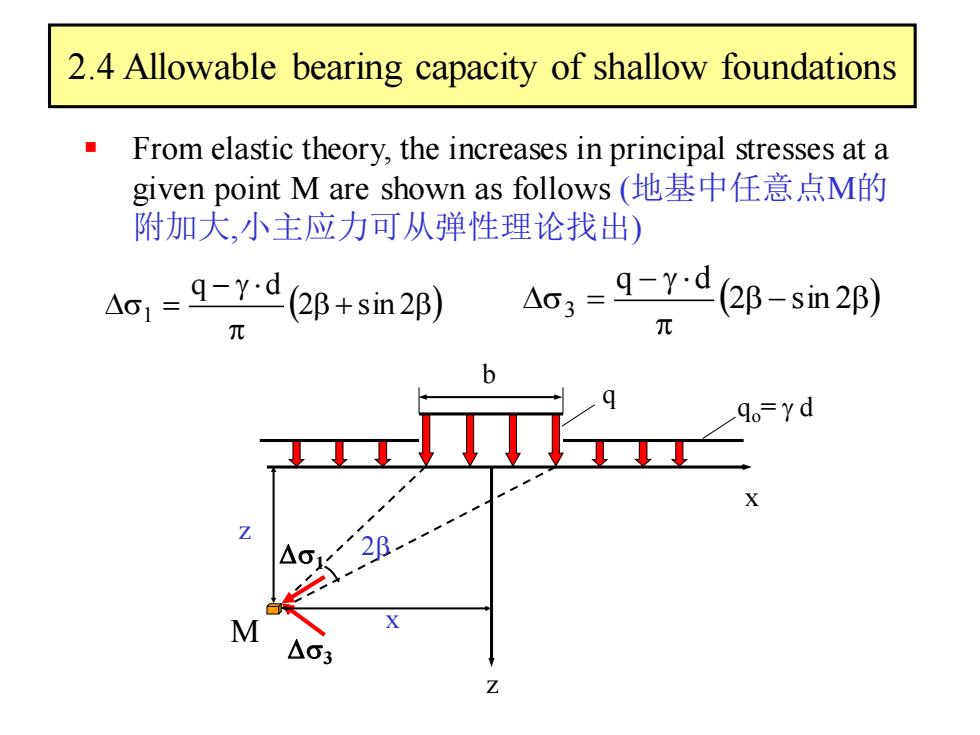
2.4 Allowable bearing capacity of shallow foundations From elastic theory,the increases in principal stresses at a given point M are shown as follows(地基中任意点M的 附加大,小主应力可从弹性理论找出) -dB+sin2B) Ac3=9-Y:d(2B-sin2B) 元 元 03
2.4 Allowable bearing capacity of shallow foundations ▪ From elastic theory, the increases in principal stresses at a given point M are shown as follows (地基中任意点M的 附加大,小主应力可从弹性理论找出) b x z z 2b q 1 3 x qo= d M ( b + b) − = 2 sin 2 q d 1 ( b − b) − = 2 sin 2 q d 3

2.4 Allowable bearing capacity of shallow foundations Assume the coefficient of earth pressure at-rest(K)is 1, the increments in principal stresses can be superimposed to the principal stresses.The final principal stresses at depth z are(假设静止土压力系数K=l,这样自重应力 与附加应力可以在任意方向叠加,地基中任意点M的大 小主应力可从以下公式找出) o-9p+sn2p++d c;-9-Y-d(2B-sin2p)+y(z+d)
2.4 Allowable bearing capacity of shallow foundations ▪ Assume the coefficient of earth pressure at-rest (Ko ) is 1, the increments in principal stresses can be superimposed to the principal stresses. The final principal stresses at depth z are (假设静止土压力系数Ko =1,这样自重应力 与附加应力可以在任意方向叠加,地基中任意点M的大 小主应力可从以下公式找出 ) (2 sin 2 ) (z d) q d 1 b + b + + − = (2 sin 2 ) (z d) q d 3 b − b + + − =

2.4 Allowable bearing capacity of shallow foundations When the stresses in point M reach the limiting equilibrium,o and o3 at failure are related by the following expression from Mohr-Coulomb failure criteria (当M点达到极限平衡状态时,大小主应力必需满足以 下公式) =a5+2如m5号》 z is depth of the plastic zone and is expressed as a function of B(z为塑性区深度,是β的函数) z=9-Yd sin2B --d Y·π sinφ y.tanΦ
2.4 Allowable bearing capacity of shallow foundations ▪ When the stresses in point M reach the limiting equilibrium, 1 and 3 at failure are related by the following expression from Mohr-Coulomb failure criteria (当M点达到极限平衡状态时,大小主应力必需满足以 下公式) + + = + 2 2c tan 45 2 tan 45 2 1 3 d tan c 2 sin q d sin 2 z − − − b b − = ▪ z is depth of the plastic zone and is expressed as a function of b (z为塑性区深度,是b的函数)