
Section 3.1 Norms and System Gains Computation of System Norms Suppose that T(s)is strictly proper and has no poles on the imaginary axis.We have Irs服=2 ITGuP d. T(-s)T(s)ds 手T-re6 By residue theorem,T(s)equals the sum of the residues of T(-s)T(s)at its poles in the LHP. 4口,+@,4定4=定0C Zhang.W.D..CRC Press.2011 Version 1.0 7/69
Section 3.1 Norms and System Gains Computation of System Norms Suppose that T(s) is strictly proper and has no poles on the imaginary axis. We have kT(s)k 2 2 = 1 2π Z ∞ −∞ |T(jω)| 2 dω = 1 2πj Z j∞ −j∞ T(−s)T(s) ds = 1 2πj I T(−s)T(s) ds By residue theorem, kT(s)k 2 2 equals the sum of the residues of T(−s)T(s) at its poles in the LHP. Zhang, W.D., CRC Press, 2011 Version 1.0 7/69
Section 3.1 Norms and System Gains Example Take T(s)=1/(s+1).The LHP pole of T(-s)T(s)is at s=-1.The residue at this pole equals +号 11 Hence lT(s)ll2=1/V2 The oo-norm can be computed by search.Choose a series of frequency points for T(s): ,n} The estimate for T(s)is max [T(wk)引 1<k<n 4口,+@,4定4=定0C Zhang.W.D..CRC Press.2011 Version 1.0 8/69
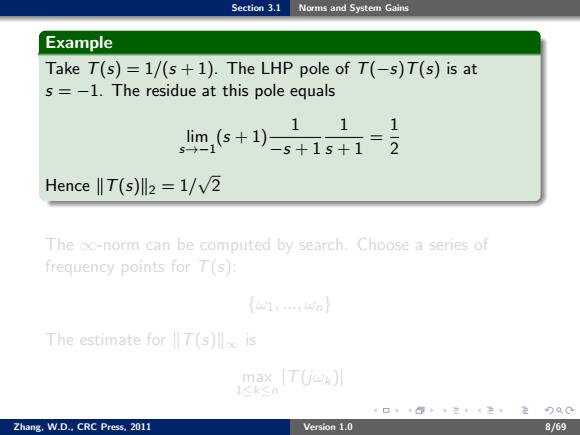
Section 3.1 Norms and System Gains Example Take T(s) = 1/(s + 1). The LHP pole of T(−s)T(s) is at s = −1. The residue at this pole equals lim s→−1 (s + 1) 1 −s + 1 1 s + 1 = 1 2 Hence kT(s)k2 = 1/ √ 2 The ∞-norm can be computed by search. Choose a series of frequency points for T(s): {ω1, ..., ωn} The estimate for kT(s)k∞ is max 1≤k≤n |T(jωk )| Zhang, W.D., CRC Press, 2011 Version 1.0 8/69

Section 3.1 Norms and System Gains Example Take T(s)=1/(s+1).The LHP pole of T(-s)T(s)is at s=-1.The residue at this pole equals +号 11 Hence lT(s)ll2 =1/V2 The oo-norm can be computed by search.Choose a series of frequency points for T(s): {w1,,wn} The estimate for T(s)loo is max IT(jwk)I 1≤k≤n 4口,+@,4定4=定0C Zhang.W.D..CRC Press.2011 Version 1.0 8/69
Section 3.1 Norms and System Gains Example Take T(s) = 1/(s + 1). The LHP pole of T(−s)T(s) is at s = −1. The residue at this pole equals lim s→−1 (s + 1) 1 −s + 1 1 s + 1 = 1 2 Hence kT(s)k2 = 1/ √ 2 The ∞-norm can be computed by search. Choose a series of frequency points for T(s): {ω1, ..., ωn} The estimate for kT(s)k∞ is max 1≤k≤n |T(jωk )| Zhang, W.D., CRC Press, 2011 Version 1.0 8/69
Section 3.1 Norms and System Gains Properties of System Norms Property 1 of 2-norm: If T(s)is stable,by Parseval's theorem: lIT(s)ll2 IIT(t)ll2 Property 2 of 2-norm: Assume that the complex conjugate of c=a+bi is c=a-bi Theorem If Ti(s)does not have poles in Re s>0 while Ta(s)does not have poles in Re s<0,then (S+T2s修=(s修+T(⑤呢 4口,+@,4定4定0C Zhang,W.D..CRC Press.2011 Version 1.0 9/69
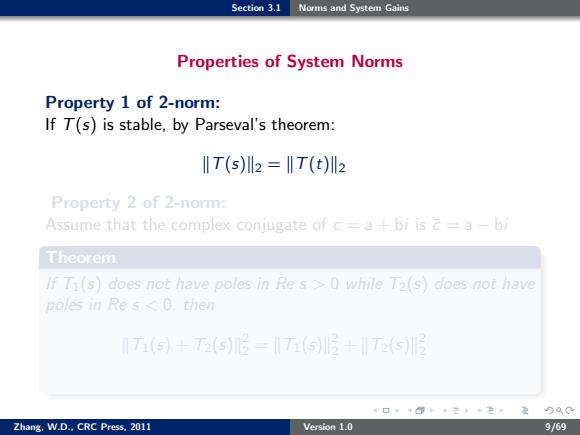
Section 3.1 Norms and System Gains Properties of System Norms Property 1 of 2-norm: If T(s) is stable, by Parseval’s theorem: kT(s)k2 = kT(t)k2 Property 2 of 2-norm: Assume that the complex conjugate of c = a + bi is ¯c = a − bi Theorem If T1(s) does not have poles in Re s > 0 while T2(s) does not have poles in Re s < 0, then kT1(s) + T2(s)k 2 2 = kT1(s)k 2 2 + kT2(s)k 2 2 Zhang, W.D., CRC Press, 2011 Version 1.0 9/69

Section 3.1 Norms and System Gains Properties of System Norms Property 1 of 2-norm: If T(s)is stable,by Parseval's theorem: ‖T(s)l2=‖T(t)2 Property 2 of 2-norm: Assume that the complex conjugate of c=a+bi is c=a-bi Theorem If Ti(s)does not have poles in Res>0 while T2(s)does not have poles in Re s <0,then IT1(s)+T2(s)3=T五1(s)3+川T2(s)2 4口,484定4生,定QC Zhang.W.D..CRC Press.2011 Version 1.0 9/69
Section 3.1 Norms and System Gains Properties of System Norms Property 1 of 2-norm: If T(s) is stable, by Parseval’s theorem: kT(s)k2 = kT(t)k2 Property 2 of 2-norm: Assume that the complex conjugate of c = a + bi is ¯c = a − bi Theorem If T1(s) does not have poles in Re s > 0 while T2(s) does not have poles in Re s < 0, then kT1(s) + T2(s)k 2 2 = kT1(s)k 2 2 + kT2(s)k 2 2 Zhang, W.D., CRC Press, 2011 Version 1.0 9/69