1±e/√1-2之间,如图32所示。包络线收敛速率取决于50。(特征根实部之模) 响应的阻尼振荡频率取决于√1-20。(特征根虚部)。响应的初始值h(0)=0,初始斜率 h'(0)=0,终值h(o)=1。 2.3.4.5.6.7.8,1.0 图3-11二阶系统单位阶跃响应 >图311的绘制程序 zta=00.1020.30.40.50.60.70.81.02.01 for i= ( xlabel('wnt).ylabel(h(t)); title'zeta=0,1,2,3,45,.6.7,8,1.0,2.0,gmid 一12欠阻尼二阶系饶单位跃响应及包
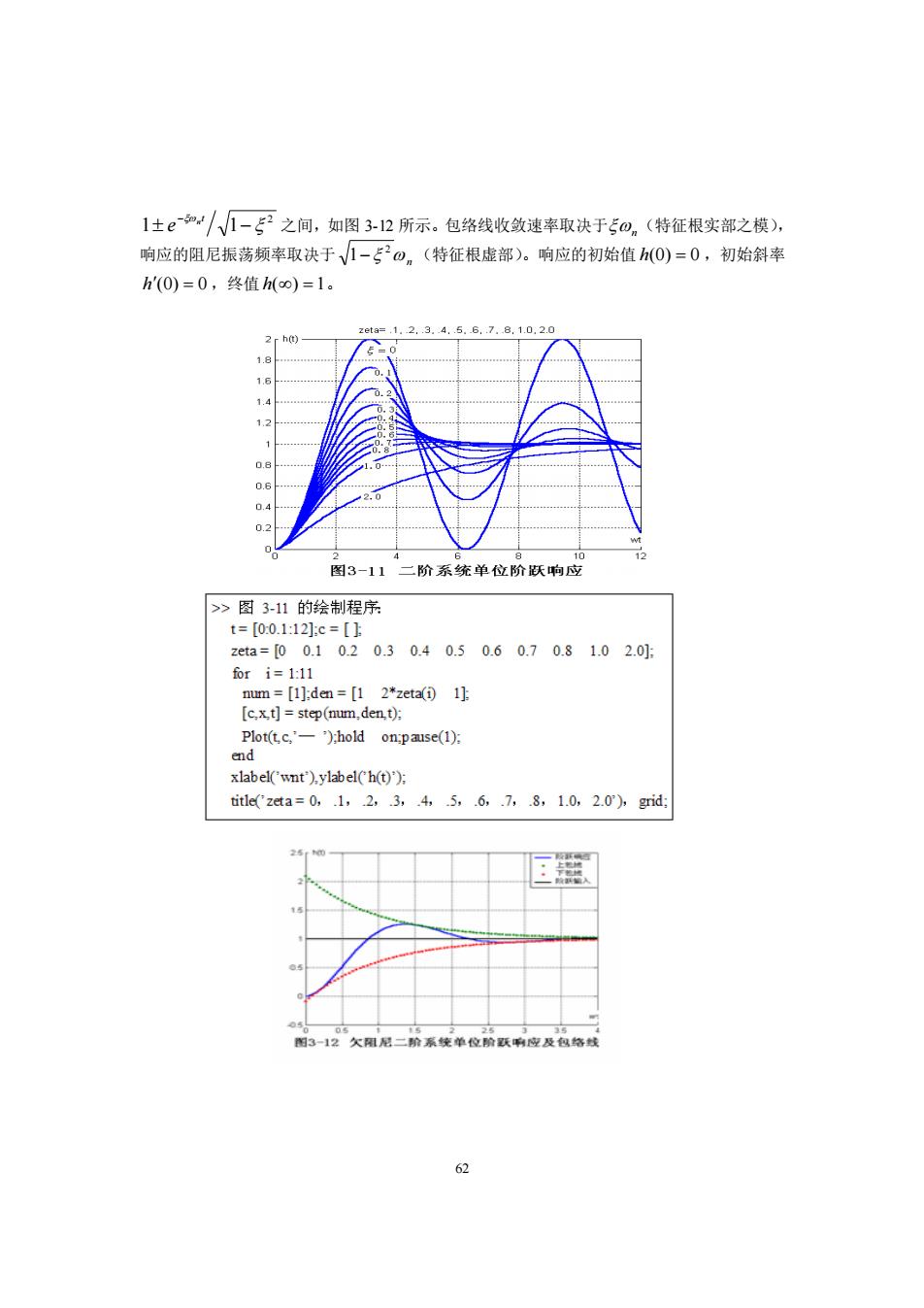
62 2 1 1 − − t n e 之间,如图 3-12 所示。包络线收敛速率取决于 n (特征根实部之模), 响应的阻尼振荡频率取决于 n 2 1− (特征根虚部)。响应的初始值 h(0) = 0 ,初始斜率 h(0) = 0 ,终值 h() = 1

>图3-12的绘制程序: m=2.5:zeta=0.4;te[0:0.05:4] t1 acos(zeta)*ones(1,length(t)). al =(1/sqrt(1-zeta"2)); hl 1-al*exp(-zeta*m*t).*sin(wn*sqrt(1-zeta"2)*t+t1); bu al*exp(-zetatwmn*t)+1;b1=2-bu; plot(t,hi,'-',t,bu,'.',t,bl,'.',t,ones(size(t)),'k-');grid xlabel('mt'),ylabel('h(t)'); 3 欠阻尼二阶系统动态性能指标计算 (1)峰值时间1。:令h)=k()=0,利用式(3-11)可得 snV1-5o,1=0 即有 V1-5201=0,π,2元,3π,… 由图3-1,并根据峰值时间定义,可得 ,-50 (3-12) (2)超调量σ%:将式(3-12)代入式(3-10)整理后可得 h(tp)=1+e a%-,)-Mox100%=e/Fx100% (3-13) h(co) 可见,典型欠阻尼二阶系统的超调量σ只与阻尼比5有关,两者的关系如图313所示
63 . 3 欠阻尼二阶系统动态性能指标计算 (1)峰值时间 p t :令 h(t) = k(t) = 0 ,利用式(3-11)可得 sin 1 0 2 − n t = 即有 1− 2 n t = 0, , 2, 3 , 由图 3-1,并根据峰值时间定义,可得 n p t 2 1− = (3-12) (2)超调量 0 0 :将式(3-12)代入式(3-10)整理后可得 2 1 ( ) 1 − − h t = + e p % 100 ( ) ( ) ( ) − = h h t p h % 2 − 1− = e 100 % (3-13) 可见,典型欠阻尼二阶系统的超调量 0 0 只与阻尼比 有关,两者的关系如图 3-13 所示