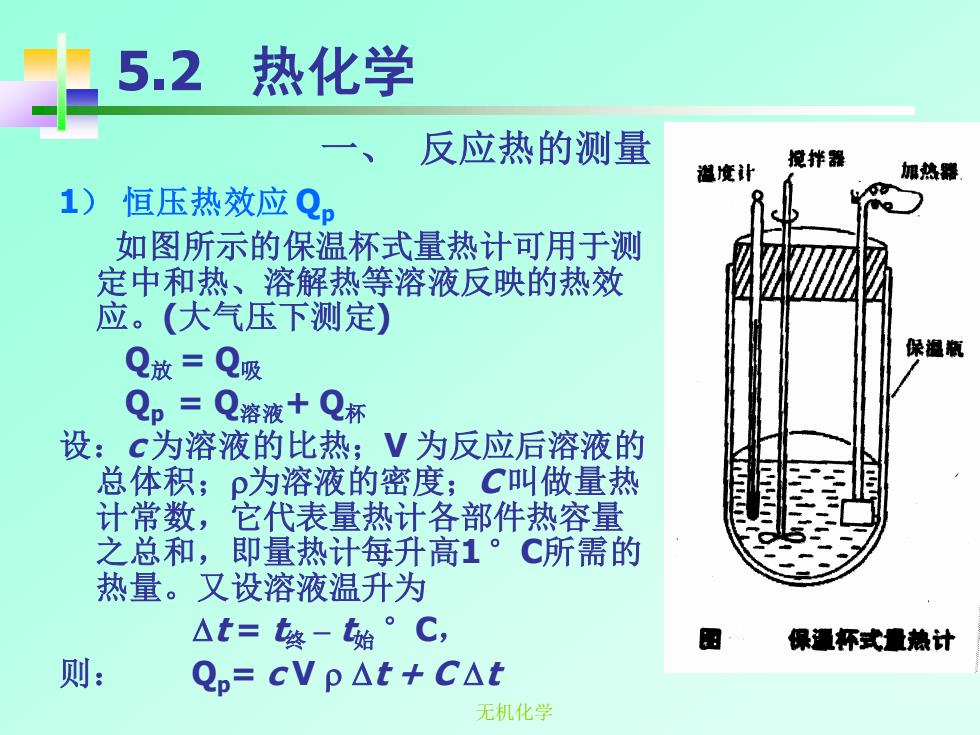
5.2 热化学 反应热的测量 搅拌器 湛度让 加热器 1) 恒压热效应Qp 如图所示的保温杯式量热计可用于测 定中和热、溶解热等溶液反映的热效 应。(大气压下测定) Q放=Q吸 Qp=Q溶液十Q标 设:c为溶液的比热;V为反应后溶液的 总体积;p为溶液的密度;,C叫做量热 计常数,它代表量热计各部件热容量 之总和,即量热计每升高1°C所需的 热量。又设溶液温升为 △t=终-始°C, 保通杯式量热计 则: Qp=cVp△t+CAt 无机化学
无机化学 5.2 热化学 1) 恒压热效应 Qp 如图所示的保温杯式量热计可用于测 定中和热、溶解热等溶液反映的热效 应。(大气压下测定) Q放 = Q吸 Qp = Q溶液+ Q杯 设:c 为溶液的比热;V 为反应后溶液的 总体积;为溶液的密度;C 叫做量热 计常数,它代表量热计各部件热容量 之总和,即量热计每升高1 °C所需的 热量。又设溶液温升为 t = t终 – t始 °C, 则: Qp= c V t + C t 一、 反应热的测量
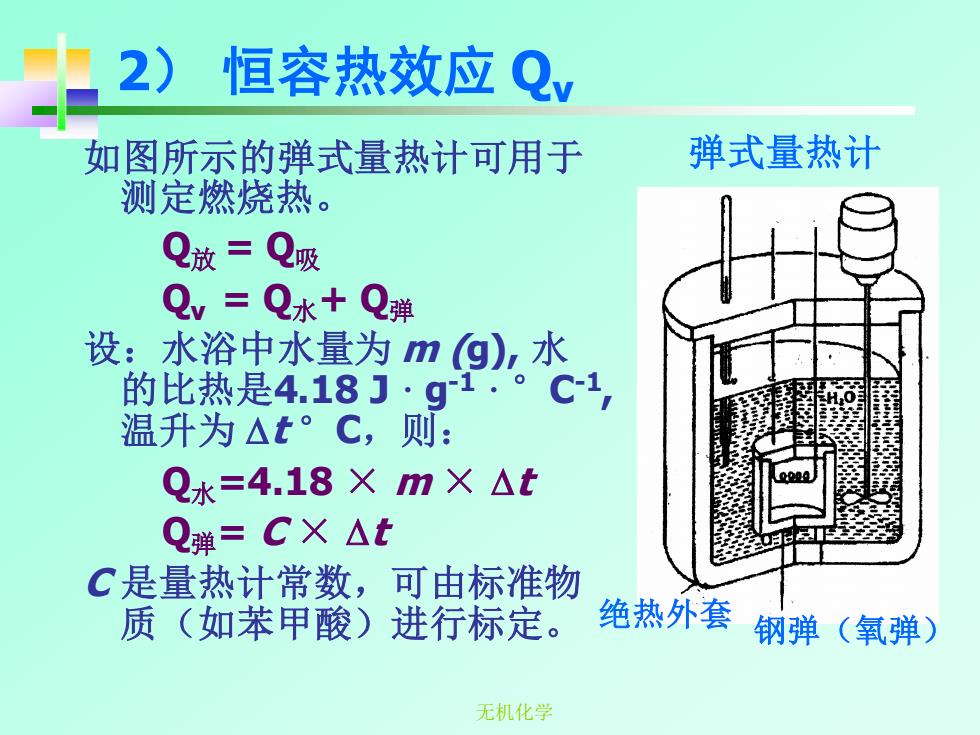
2)1 恒容热效应Qy 如图所示的弹式量热计可用于 弹式量热计 测定燃烧热。 Q放=Q吸 Qv=Q水+Q弹 设:水浴中水量为mg)水 的比热是4.18·g 1·9 1, 温升为△t。C,则: Q水=4.18×m×△t Q弹=CX△t C是量热计常数,可由标准物 质(如苯甲酸)进行标定。 绝热外套 钢弹(氧弹) 无机化学
无机化学 2) 恒容热效应 Qv 如图所示的弹式量热计可用于 测定燃烧热。 Q放 = Q吸 Qv = Q水+ Q弹 设:水浴中水量为 m (g), 水 的比热是4.18 J ·g-1 ·°C-1 , 温升为 t °C,则: Q水=4.18 × m × t Q弹= C × t C 是量热计常数,可由标准物 质(如苯甲酸)进行标定。 绝热外套 钢弹(氧弹) 弹式量热计

二、焓(H)与焓变(△H)(Enthalpy) 在恒压条件下,只做体积功时,W=P△V, 则有: AU=Qp-PAV 或 Qp=△U+P△V =(U2U1)+PV2V) =(U2+PV2)-(U1+PV1) 定义:H=U+PV(焓的定义) 得:Qp=H2-H1=△H 即:△H=Qp(在数值上) (封闭体系、等压过程、只做体积功) 无机化学
无机化学 二、 焓(H)与焓变(H) (Enthalpy) ◼ 在恒压条件下,只做体积功时,W = P V, 则有: U = Qp – P V 或 Qp = U + P V = (U2 –U1) + P(V2 –V1) = (U2 + PV2) – (U1 + PV1) ◼ 定义:H U + PV (焓的定义) 得:Qp = H2 – H1 = H 即:H = Qp (在数值上) (封闭体系、等压过程、只做体积功)

焓与焓变 ■△H,H为状态函数。 △H反映了化学反应的热效应。 △H为广度量(容量性质),即与物质的量有关系的量。 (强度量:与物质的量无关系的量,无加合性。如温度) ■在恒容条件下,△V=0,体系不做体积功(也不 做其它功),即W=O, 此时,热力学第一定律可表示为: △U=Qy 在此条件下,体系吸收的热量,只用于改变内能。 无机化学
无机化学 焓与焓变 ◼ H,H 为状态函数。 H 反映了化学反应的热效应。 H 为广度量(容量性质),即与物质的量有关系的量。 (强度量:与物质的量无关系的量,无加合性。如温度) ◼ 在恒容条件下, V = 0, 体系不做体积功(也不 做其它功), 即 W = 0, 此时,热力学第一定律可表示为: U = QV 在此条件下,体系吸收的热量,只用于改变内能

三、利用焓变计算内能改变量 ■在101.3kPa和100°C条件下,反应: H2(g)+02(g)=H20(g) 的△H=-241.8kJ/mol,求△U. ■解:△U=△H-P△V 恒温、恒压过程,PAV=△ngRT △ng为产物和反应物气体的量之差。 △U=AH-△ngRT =-241.8-[(1-1.5)×8.31×10-3×373] =-241.8-(-1.50)=-240(kJ/mol) ■可以看出,△n。RT项相对于△H项数值小得多,一般来 说可以用△H来近似估算AU。(Qp≈Qv) 无机化学
无机化学 三、利用焓变计算内能改变量 ◼ 在101.3 kPa 和100 °C 条件下,反应: H2(g) + O2(g) = H2O(g) 的 H = -241.8 kJ/mol, 求U. ◼ 解:U = H – PV 恒温、恒压过程, PV = ng RT ng 为产物和反应物气体的量之差。 U = H – ng RT = -241.8 –[(1 –1.5)×8.31 ×10-3 ×373] = -241.8 – (-1.50) = -240 (kJ/mol) ◼ 可以看出, ng RT项相对于H 项数值小得多,一般来 说可以用H 来近似估算U。(Qp Qv)