
国家重点实验室 Symmetry assumption and Capacity o Assume that the channel has "input-output symmetry. (Example:BSC,BEC) BEC(c) 0 1-9 0 (Symmetric)Capacity 1 1-c For channels with I/O symmetry,the capacity is given by C(W)≌I(X;Y) with X unif.(0,1) =∑∑)W0y川x)log W(yx) eeX2 W(y川0)+,W0y1D) 2 Use base-2 logarithms: 0≤C(W)≤1 6
Symmetry assumption and Capacity Assume that the channel has “input-output symmetry.” (Example: BSC, BEC) (Symmetric) Capacity For channels with I/O symmetry, the capacity is given by Use base-2 logarithms: 6 ( ) ( ; ) with unif. {0,1} 1 (|) ( | )log 2 1 1 ( | 0) ( |1) 2 2 y Yx X CW I X Y X Wyx Wyx W y W y ∈ ∈ = + 0 ()1 ≤ ≤ C W

国家重点实验室 Symmetry assumption and Capacity o Bhattacharyya parameter Z(wW)兰∑√W(y10)w(y1西 o The parameters C(W)and Z(W)are used as measures of rate and reliability. Define the decision region for message m,D=yAIf(y)=m For codes with two codewords,the error probability,when message 2 is transmitted,is P.(eI2)=∑Pw(ylx2) yeD For yeD1,Py(ylx)P(ylx2)for ML decoding 。经过简单处理,有P.(2)≤∑VRyx)R) yeD 进而P,(em)≤∑VP(yIx)P(y) known as the Bhattacharyya bound on error probability 7
Symmetry assumption and Capacity Bhattacharyya parameter The parameters C(W) and Z(W) are used as measures of rate and reliability. Define the decision region for message m, For codes with two codewords, the error probability, when message 2 is transmitted, is 经过简单处理,有 进而 7 ( ) ( | 0) ( |1) y Y ZW W y W y ∈ { | () } N m Y =∈ = y y f m 1 2 ( | 2) ( | ) Pe P B N ∈ = y y x For y ∈ 1, for ML decoding 1 2 (| ) (| ) P P N N yx yx ≥ 1 1 2 ( | 2) ( | ) ( | ) Pe P P B NN ∈ ≤ y y x y x 1 2 ( | ) ( | ) ( | ) P em P P B NN ≤ y y x y x known as the Bhattacharyya bound on error probability

国家重点实验室 Main idea for channel polarization Channel coding problem trivial for two types of channels Perfect:C(W)=1 Useless:C(W)=0 Transform ordinary W into such extreme channels >Perfect channels:C(W)=1,the output Y determines the input X Useless channels:C(W)=0,the output Y is independent of the input X o Channel polarization is a technique to convert any binary-input channel into a mixture of binary-input extreme channels
Main idea for channel polarization Perfect channels: C(W)=1, the output Y determines the input X Useless channels: C(W)=0, the output Y is independent of the input X Channel polarization is a technique to convert any binary-input channel into a mixture of binary-input extreme channels 8
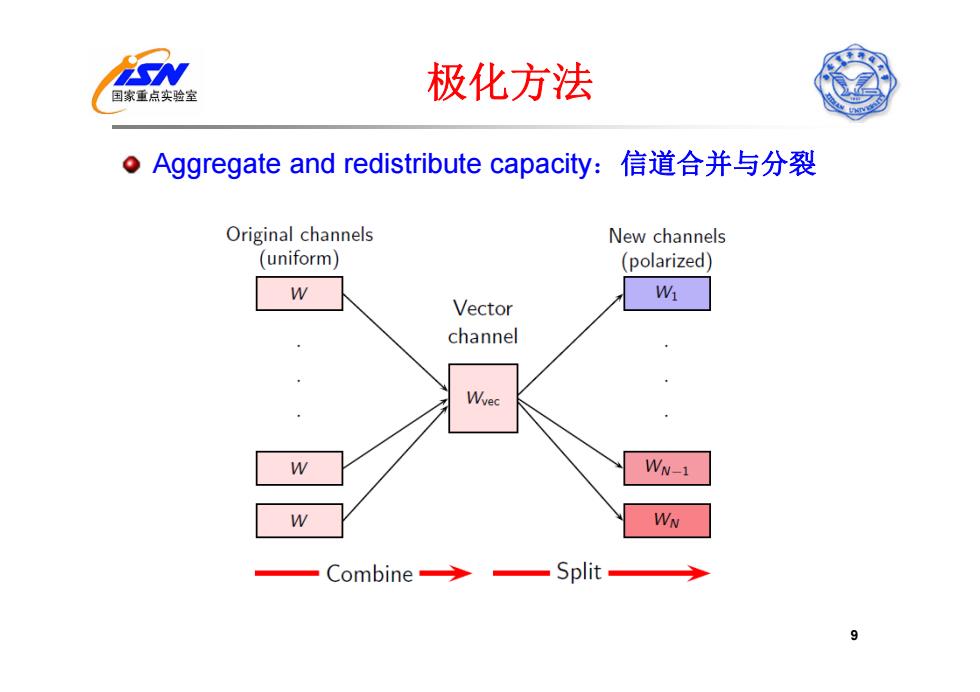
国家重点实验室 极化方法 。Aggregate and redistribute capacity:信道合并与分裂 Original channels New channels (uniform) (polarized) Wi Vector channel Wvec W WN-1 W WN Combine→ Split 9
极化方法 Aggregate and redistribute capacity:信道合并与分裂 9

国家重点实验室 Channel Combining 0 Begin with N copies of W >Use a 1-1 mapping Gw:{0,1W→{0,1} UNA IN-1 >to create a vector channel UN W:UN→YW oCombining operation is lossless: >Let U.Uv i.i.d.-Unif.01 then X,.Xy i.i.d.~Unif.(01) >and C(W)=I(UN;YN) =I(XN:YN) =NC(W) 10
Channel Combining Begin with N copies of W Use a 1-1 mapping to create a vector channel Combining operation is lossless: Let then and 10 :{0,1} {0,1 } N N GN → : N N WU Y N → 1,., i.i.d. Unif. {0,1} U UN 1,., i.i.d. Unif. {0,1} X X N () (;) ( ; ) ( ) N N N N N CW IU Y I X Y NC W = = =