
clMSc5706TopicsinTheoreticalcomputerScience Week 2:Linear Programming Instructor:Shengyu Zhang 1
Instructor: Shengyu Zhang 1

LP Motivating examples Introduction to algorithms Simplex algorithm On a particular example General algorithm Duality An application to game theory 2
LP ◼ Motivating examples ◼ Introduction to algorithms ◼ Simplex algorithm ❑ On a particular example ❑ General algorithm ◼ Duality ◼ An application to game theory 2

Example 1:profit maximization A company has two types of products:P,Q. ■Profit:P--$1each; Q---$6 each ■Constraints: Daily productivity (including both P and Q)is 400 Daily demand for P is 200 Daily demand for Q is 300 Question:How many P and O should we produce to maximize the profit? x1 units of P,xz units of Q 3
Example 1: profit maximization ◼ A company has two types of products: P, Q. ◼ Profit: P --- $1 each; Q --- $6 each. ◼ Constraints: ❑ Daily productivity (including both P and Q) is 400 ❑ Daily demand for P is 200 ❑ Daily demand for Q is 300 ◼ Question: How many P and Q should we produce to maximize the profit? ❑ 𝑥1 units of P, 𝑥2 units of Q 3

How to solve? ■x1 units of P Variables: x2 units of Q 口x1andx2. Constraints: Constraints: Daily productivity (including 口x1+x2≤400 both P and Q)is 400 x1≤200 Daily demand for P is 200 口 x2≤300 Daily demand for Q is 300 x1,X2≥0 Question:how much P Objective: and Q to produce to max x1+6x2 maximize the profit? 4
How to solve? ◼ 𝑥1 units of P 𝑥2 units of Q ◼ Constraints: ❑ Daily productivity (including both P and Q) is 400 ❑ Daily demand for P is 200 ❑ Daily demand for Q is 300 ◼ Question: how much P and Q to produce to maximize the profit? ◼ Variables: ❑ 𝑥1 and 𝑥2. ◼ Constraints: ❑ 𝑥1 + 𝑥2 ≤ 400 ❑ 𝑥1 ≤ 200 ❑ 𝑥2 ≤ 300 ❑ 𝑥1, 𝑥2 ≥ 0 ◼ Objective: max 𝑥1 + 6𝑥2 4
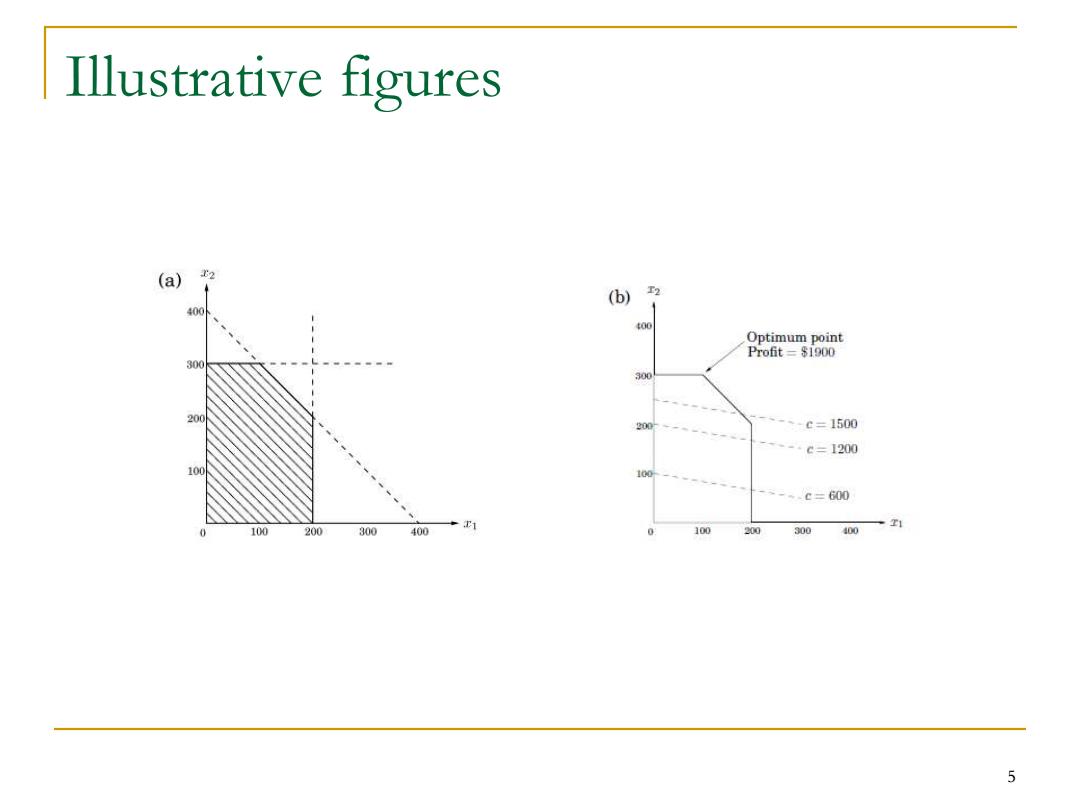
Illustrative figures (a) 2 (b) T2 400 400 Optimum point Profit=$1900 300 300 200 200 -、-、-c=1500 ----c=1200 5-.c=600 E1 100 200 300 400 100 200 300 400 1 5
Illustrative figures 5