
Deterministic Policy and Stochastic Policy Deterministic Policy:S-A,(s)=a Stochastic Policy:π:S×A→[0,1],π(a|s)∈0,1] ~Dynamic programming algorithms初始输入可以是stochastic policy但返回总是一个deterministic policy ~有没有可能存在optimal policyπ*,它是stochastic policy, 并且对所有deterministic policy',Vx*>Vx? "Markov Decision Process-Discrete Stochastic Dynamic Programming"by Martin L.Puterman(John Wilson and Sons Ed.).It is proved that if the reward function is deterministic, the optimal policy exists and is also deterministic. ~反证法,假定一个stochastic policyπ*是最优的,并且不存 在deterministic policy大于等于它的期望效用。当π*在用概 率选择两个行动时,总可以选后续效用较大的那个行动:当 两者后续效用相等,就固定的选一个 口46t1三+1=,是9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Deterministic Policy and Stochastic Policy ▶ Deterministic Policy: π : S → A, π(s) = a ▶ Stochastic Policy: π : S × A → [0, 1], π(a | s) ∈ [0, 1] ▶ Dynamic programming algorithms 初始输入可以是 stochastic policy 但返回总是一个 deterministic policy ▶ 有没有可能存在 optimal policy π ∗,它是 stochastic policy, 并且对所有 deterministic policy π ′,Vπ∗ > Vπ′? ▶ “Markov Decision Process – Discrete Stochastic Dynamic Programming” by Martin L. Puterman (John Wilson and Sons Ed.). It is proved that if the reward function is deterministic, the optimal policy exists and is also deterministic. ▶ 反证法,假定一个 stochastic policy π ∗ 是最优的,并且不存 在 deterministic policy 大于等于它的期望效用。当 π ∗ 在用概 率选择两个行动时,总可以选后续效用较大的那个行动;当 两者后续效用相等,就固定的选一个
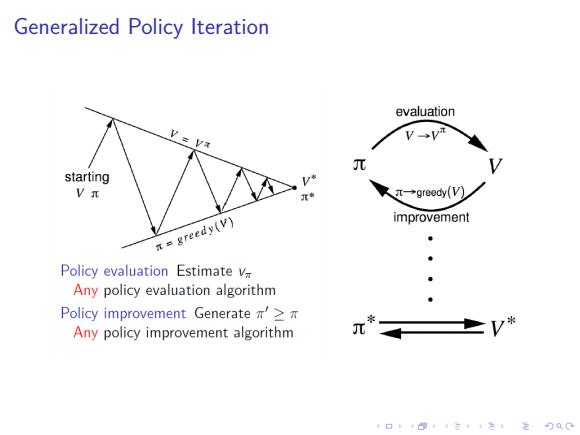
Generalized Policy Iteration evaluation 元 starting V t→greedy(V) improvement as greedy(v) Policy evaluation Estimate v Any policy evaluation algorithm Policy improvement Generate ' Any policy improvement algorithm 口卡回·三4色,是分Q0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Generalized Policy Iteration

Table of Contents 背景 MDPs 强化学习问题 蒙特卡洛方法(Monte Carlo Methods 蒙特卡洛预测(Monte Carlo Prediction】 蒙特卡洛控制(Monte Carlo Control) 时序差分学习(Tempora-Difference Learning 时序差分预测(TD Prediction 时序差分控制(TD Control Sarsa:on-policy Q-learning:off-policy 策略梯度(Policy Gradient Monte-Carlo Policy Gradient Actor-Critic Policy Gradient 深度强化学习 Deep Q-Networks (DQN Policy Gradients for Deep Reinforcement Learning 4口卡404三·1怎生0C
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Table of Contents 背景 MDPs 强化学习问题 蒙特卡洛方法 (Monte Carlo Methods) 蒙特卡洛预测(Monte Carlo Prediction) 蒙特卡洛控制(Monte Carlo Control) 时序差分学习 (Temporal-Difference Learning) 时序差分预测(TD Prediction) 时序差分控制(TD Control) Sarsa:on-policy Q-learning : off-policy 策略梯度 (Policy Gradient) Monte-Carlo Policy Gradient Actor-Critic Policy Gradient 深度强化学习 Deep Q-Networks (DQN) Policy Gradients for Deep Reinforcement Learning
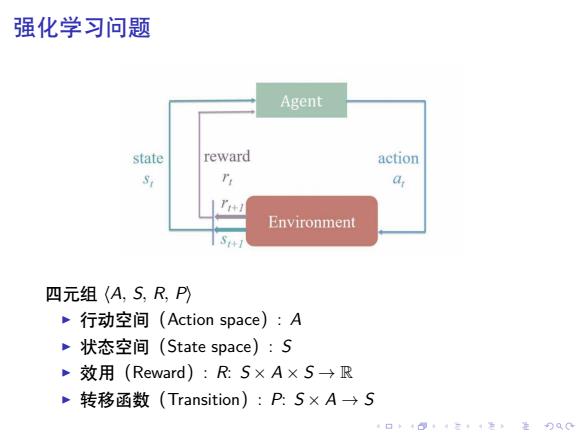
强化学习问题 Agent state reward action a Environment S 四元组(A,S,R,P) P行动空间(Action space):A ,状态空间(State space):S 子 效用(Reward):R:S×A×S→R 转移函数(Transition):P:S×A→S 口◆401三1,是90C
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 强化学习问题 四元组 ⟨A, S, R, P⟩ ▶ 行动空间(Action space): A ▶ 状态空间(State space): S ▶ 效用(Reward): R: S × A × S → R ▶ 转移函数(Transition): P: S × A → S

强化学习问题 Agent's policy:T(a s)=P[At=a St=s π:S×A→R, ∑x(a|s)=1 a∈A 对于确定策略,π:S)A Agent's view: s0,a0,1,51,a1,2,S2,a2,3,53,. π*(s)→a,i20 Agent's goal:learn a policy to maximize long-term total reward T-step: 0 discounted: t=1 4口◆4⊙t1三1=,¥9QC
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 强化学习问题 ▶ Agent’s policy: π(a | s) = P[At = a | St = s] π : S × A → R, ∑ a∈A π(a | s) = 1 对于确定策略,π : S → A ▶ Agent’s view: s0, a0,r1,s1, a1,r2,s2, a2,r3,s3, . . . π ∗ (si) → ai , i ≥ 0 ▶ Agent’s goal: learn a policy to maximize long-term total reward T-step: ∑ T t=1 rt discounted: ∑∞ t=1 γ t rt