State-Value Function and Action-Value Function (con't) V(s)与Q(s,a)之间的关系 V.(s=∑π(als)Qx(s,a) aEA Q(s,a)=Rs,a)+∑Ts,a,s)V.(⑤) sES qr(s,a)8,a U(s)←Hs qm(s,a)←-a● u(s)HsC 4口◆4⊙t1三1=,¥9QC
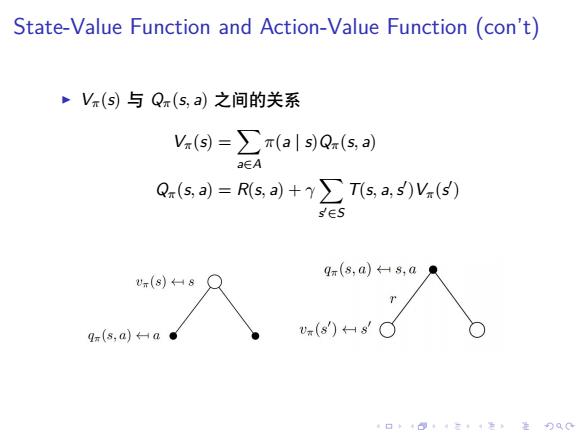
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . State-Value Function and Action-Value Function (con’t) ▶ Vπ(s) 与 Qπ(s, a) 之间的关系 Vπ(s) = ∑ a∈A π(a | s)Qπ(s, a) Qπ(s, a) = R(s, a) + γ ∑ s ′∈S T(s, a,s ′ )Vπ(s ′ )
Bellman Equations ~Vπ自身的递推关系 -ga19(so+会sa网) a∈A ·Q。自身的递推关系: Q(s,)=Rs,a)+y∑Tsa,s)∑π(a'1s)Q(5,a) s∈S a∈A gm(8,a)8,a .(88 q(s,d)a 4口◆4⊙t4三1=,¥9QC
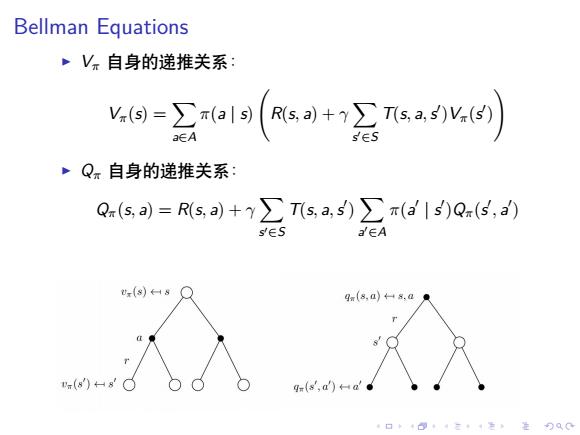
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bellman Equations ▶ Vπ 自身的递推关系: Vπ(s) = ∑ a∈A π(a | s) ( R(s, a) + γ ∑ s ′∈S T(s, a,s ′ )Vπ(s ′ ) ) ▶ Qπ 自身的递推关系: Qπ(s, a) = R(s, a) + γ ∑ s ′∈S T(s, a,s ′ ) ∑ a ′∈A π(a ′ | s ′ )Qπ(s ′ , a ′ )

Bellman Equations(con't) ,最优状态值函数:最优值函数V(S)是在所有策略上的最大 值函数: V(s)=max V(s) 最优行为值函数:最优行为值函数Q*(s,a)是在所有策略上 的最大行为值函数 Q*(s,a)=max Q(s,a) V(s与Q*(s,a)之间的关系 V(s)=max V(s) =max∑x(als)Q.(s,a) aEA =max Q*(s,a) aEA 因为:MDP的optimal policy是deterministic policy,i.e, π*(S)=a 口◆4日1三1=,是90C
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bellman Equations (con’t) ▶ 最优状态值函数:最优值函数 V ∗ (s) 是在所有策略上的最大 值函数: V ∗ (s) = max π Vπ(s) ▶ 最优行为值函数:最优行为值函数 Q∗ (s, a) 是在所有策略上 的最大行为值函数 Q ∗ (s, a) = max π Qπ(s, a) ▶ V ∗ (s) 与 Q∗ (s, a) 之间的关系 V ∗ (s) = max π Vπ(s) = max π ∑ a∈A π(a | s)Qπ(s, a) = max a∈A Q ∗ (s, a) 因为:MDP 的 optimal policy 是 deterministic policy, i.e., π ∗ (s) = a

Bellman Equations(con't) V(s)与Q(s,a)之间的关系 Q*(s,a)=max Qr(s,a) =(风s+头sa) =Rs,a)+y∑Ts,a,s)V(s ·V(S)自身的递推关系 V(s)=max a∈A )+2.(4) E Q*(s,a)自身的递推关系 Q"(s,a)=R(s,a)+(s.a.5)mxs) a∈A sES
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Bellman Equations (con’t) ▶ V ∗ (s) 与 Q∗ (s, a) 之间的关系 Q ∗ (s, a) = max π Qπ(s, a) = max π ( R(s, a) + γ ∑ s ′∈S T(s, a,s ′ )Vπ(s ′ ) ) = R(s, a) + γ ∑ s ′∈S T(s, a,s ′ )V ∗ (s ′ ) ▶ V ∗ (s) 自身的递推关系 V ∗ (s) = max a∈A ( R(s, a) + γ ∑ s ′∈S T(s, a,s ′ )V ∗ (s ′ ) ) ▶ Q∗ (s, a) 自身的递推关系 Q ∗ (s, a) = R(s, a) + γ ∑ s ′∈S T(s, a,s ′ ) max a ′∈A Q ∗ (s ′ , a ′ )

Dynamic Programming Algorithm Iterative Policy Evaluation Policy Iteration Value lteraton iHa○ n)。 8 Bellman Beliman Expectation Bellman Expectation Bellman Optimality E中uation Equation Equation Policy Iteration+ Equation Greedy Policy Improvement Problem Prediction Control Control 口卡B·三4色进分双0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Dynamic Programming