
P260 二因素随机区组设计的平方和与均方 变异来源 DF SS MS 区组 r-1 ∑T MS ab 处理组合 ab-1 SS ∑T _C MSt A a-1 SSA ∑T MSA -C B b-1 rb MSB ∑T AXB (a-1)b-1) SSB .-C ra MSAXB 误差 (r-1)(ab-1) SSAB =SS,-SSA-SSB MSe SS。=SSr-SS,-SS, 总变异 rab-1 SS,=∑x2M-C
P260 二因素随机区组设计的平方和与均方 变异来源 DF SS MS 区组 r -1 MSr 处理组合 ab -1 MSt A a -1 MSA B b - 1 MSB A×B (a-1)(b-1) MSA×B 误差 (r-1)(ab-1) MSe 总变异 rab-1 SS x C SS SS SS SS SS SS SS SS C ra T SS C rb T SS C r T SS C ab T SS hij T e T r t A B t A B B B A A t t r r = − = − − = − − = − = − = − = − 2 2 2 2 2

二因素随机区组的期望均方 变异 期望均方 来源 固定模型 随机模型 区组 o2e+abr2B σ2e+abo2B A G 2+rbk2 G2e+ro(x+rbo2 B G2+rak2g 2。+ro2A×B+rao2B AXB c2et rK2(AXB) c2e+roaXB 误差 o2e c2e
变异 期望均方 来源 固定模型 随机模型 区组 σ 2e+abκ2 β σ 2e+abσ2 β A σ 2 e+rbκ2 A σ 2e+rσ2 (A×B) +rbσ2 A B σ 2 e + raκ2 B σ 2 e+rσ2 (A×B) +raσ2 B A×B σ 2e+ rκ2 (A×B) σ 2e+rσ2 A×B 误差 σ 2e σ 2e 二因素随机区组的期望均方

对固定模型来说: F被测项 MS被测项 MS。 但对随机模型来说,区组变异和互作变异用误 差均方进行F测验;而A、B的变异则应用互作项的 均方进行F测验
对固定模型来说: 但对随机模型来说,区组变异和互作变异用误 差均方进行F测验;而A 、B的变异则应用互作项的 均方进行F测验。 e MS F MS 被测项 被测项 =

二因素随机区组与单因素随机区组的差别: 二因素试验的处理项可以再分解为A因素水平间、 B因素水平间和AB互作三部分: SSt=SSA+SSB+SSAXB (ab-1)=(a-1)+(b-1)+(a-1)b-1) 其中,SSt为处理平方和;SSA×B为互作项平 方和;SSA为A因素平方和;SSB为B因素平方和
二因素随机区组与单因素随机区组的差别: 二因素试验的处理项可以再分解为A因素水平间、 B因素水平间和AB互作三部分: SSt = SSA + SSB + SSA×B (ab-1)=(a-1)+(b-1)+(a-1)(b-1) 其中,SSt 为处理平方和;SSA×B 为互作项平 方和 ;SSA为A因素平方和; SSB为B因素平方和
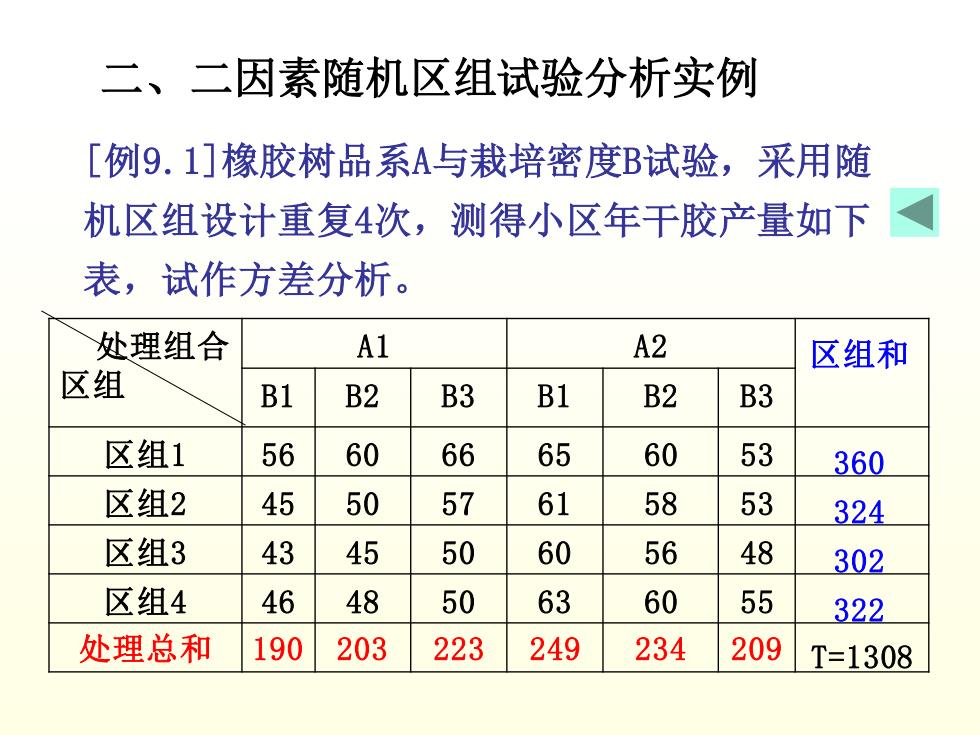
二、二因素随机区组试验分析实例 [例9.1]橡胶树品系A与栽培密度B试验,采用随 机区组设计重复4次,测得小区年干胶产量如下 表,试作方差分析。 处理组合 A1 A2 区组和 区组 B1 B2 B3 B1 B2 B3 区组1 56 60 66 65 60 53 360 区组2 45 50 57 61 58 53 324 区组3 43 45 50 60 56 48 302 区组4 46 48 50 63 60 55 322 处理总和 190 203 223 249 234 209 T=1308
[例9.1]橡胶树品系A与栽培密度B试验,采用随 机区组设计重复4次,测得小区年干胶产量如下 表,试作方差分析。 处理组合 区组 A1 A2 B1 B2 B3 B1 B2 B3 区组1 56 60 66 65 60 53 区组2 45 50 57 61 58 53 区组3 43 45 50 60 56 48 区组4 46 48 50 63 60 55 处理总和 190 203 223 249 234 209 区组和 360 324 302 322 T=1308 二、二因素随机区组试验分析实例