
Content Continuous Random Variables and PDFs Cumulative Distribution Functions Normal Random Variables Joint PDFs of Multiple Random Variables Conditioning The Continuous Bayes'Rule
Content Continuous Random Variables and PDFs Cumulative Distribution Functions Normal Random Variables Joint PDFs of Multiple Random Variables Conditioning The Continuous Bayes’ Rule

Cumulative distribution Function The cumulative distribution function,or CDF, of a random variable X is Fx(x)=P(X≤x) I∑ksx Px(k), discrete fx)dy, continuous The CDF Fx(x)“accumulates”probability“up to”the value x
Cumulative Distribution Function The cumulative distribution function, or CDF, of a random variable 𝑋 is 𝐹𝑋 𝑥 = 𝑃 𝑋 ≤ 𝑥 = 𝑘≤𝑥 𝑝𝑋 𝑘 , discrete 𝑓𝑋 𝑦 𝑑𝑦 𝑥 −∞ , continuous The CDF 𝐹𝑋 𝑥 “accumulates” probability “up to” the value 𝑥

CDF for discrete case APMF Px(x) CDF Fx(z) 1 Px(2) 0十1234 1234 PMF Px(x) CDF Fx() 1 0 0
CDF for discrete case
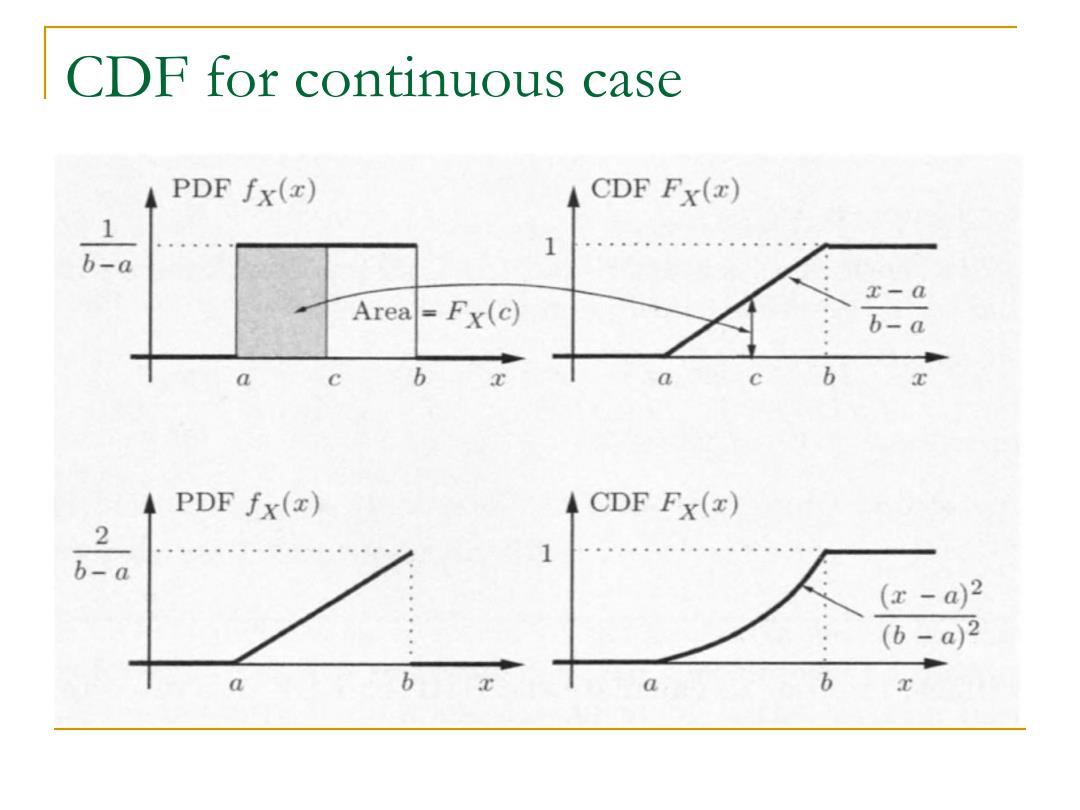
CDF for continuous case PDF fx() CDF Fx(z) 1 1 b-a x-a Area=Fx(c) b-a a b a c b PDF fx(z) CDF Fx(z) 2 1 b-a (x-a)2 (b-a)2 a b a b
CDF for continuous case

Properties Fx is monotonically increasing: ifx≤y,then Fx(x)≤Fxy): lim Fx(x)=0,lim Fx(x)=1 X→一00 X→十00 If X is discrete,Fx is piecewise constant. If X is continuous,Fx is continuous and Fx(x)= fx(t)dt, fx(x)= dFx 00
Properties 𝐹𝑋 is monotonically increasing: if 𝑥 ≤ 𝑦, then 𝐹𝑋(𝑥) ≤ 𝐹𝑋(𝑦). lim 𝑥→−∞ 𝐹𝑋(𝑥) = 0, lim 𝑥→+∞ 𝐹𝑋(𝑥) = 1 If 𝑋 is discrete, 𝐹𝑋 is piecewise constant. If 𝑋 is continuous, 𝐹𝑋 is continuous and 𝐹𝑋 𝑥 = 𝑓𝑋 𝑡 𝑑𝑡 𝑥 −∞ , 𝑓𝑋 𝑥 = 𝑑𝐹𝑋 𝑑𝑥 𝑥