
Example:Uniform Consider a uniform random variable with PDF 1 1)- ifa≤x≤b 0, otherwise 即x刘=xk=。x2 a+b 2 Ex]=☆器adx=品。x8l8 a2+ab+b2 3 Var[X]E[X2]-E[X]2 =(b-a)2 12
Example: Uniform Consider a uniform random variable with PDF 𝑓𝑋 𝑥 = 1 𝑏 − 𝑎 , if 𝑎 ≤ 𝑥 ≤ 𝑏 0, otherwise 𝐄 𝑋 = 𝑥 ∙ 1 𝑏−𝑎 𝑑𝑥 𝑏 𝑎 = 1 𝑏−𝑎 ∙ 1 2 𝑥 2 𝑏 𝑎 = 𝑎+𝑏 2 . 𝐄 𝑋 2 = 𝑥 2 𝑏−𝑎 𝑑𝑥 𝑏 𝑎 = 1 𝑏−𝑎 ∙ 1 3 𝑥 3 𝑏 𝑎 = 𝑎 2+𝑎𝑏+𝑏 2 3 . 𝐕𝐚𝐫 𝑋 = 𝐄 𝑋 2 − 𝐄 𝑋 2 = (𝑏−𝑎) 2 12
Example:Exponential An exponential random variable has PDF f=6. e-, ifx≥0 otherwise ■Note:fx(0)=λ. A fx(x) fx(x) 入 入 small入 large入 0 x
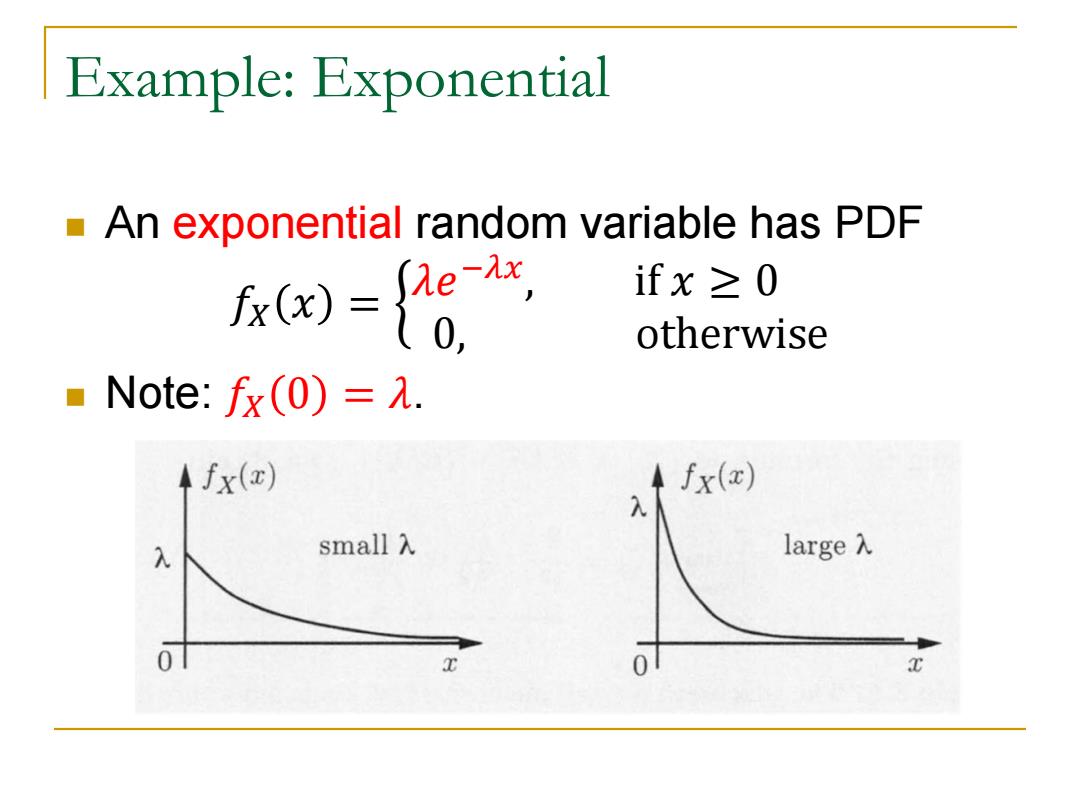
Example: Exponential An exponential random variable has PDF 𝑓𝑋 𝑥 = 𝜆𝑒 −𝜆𝑥 , if 𝑥 ≥ 0 0, otherwise Note: 𝑓𝑋 0 = 𝜆
Example:Exponential ■Note:exdx=-ex|=1. 口d(e-x)/dx=-λe-x. Tail:P(X z a)=f e-Axdx=-e=e-Aa A fx(x) Afx(a) 入 small入 large入 0 x
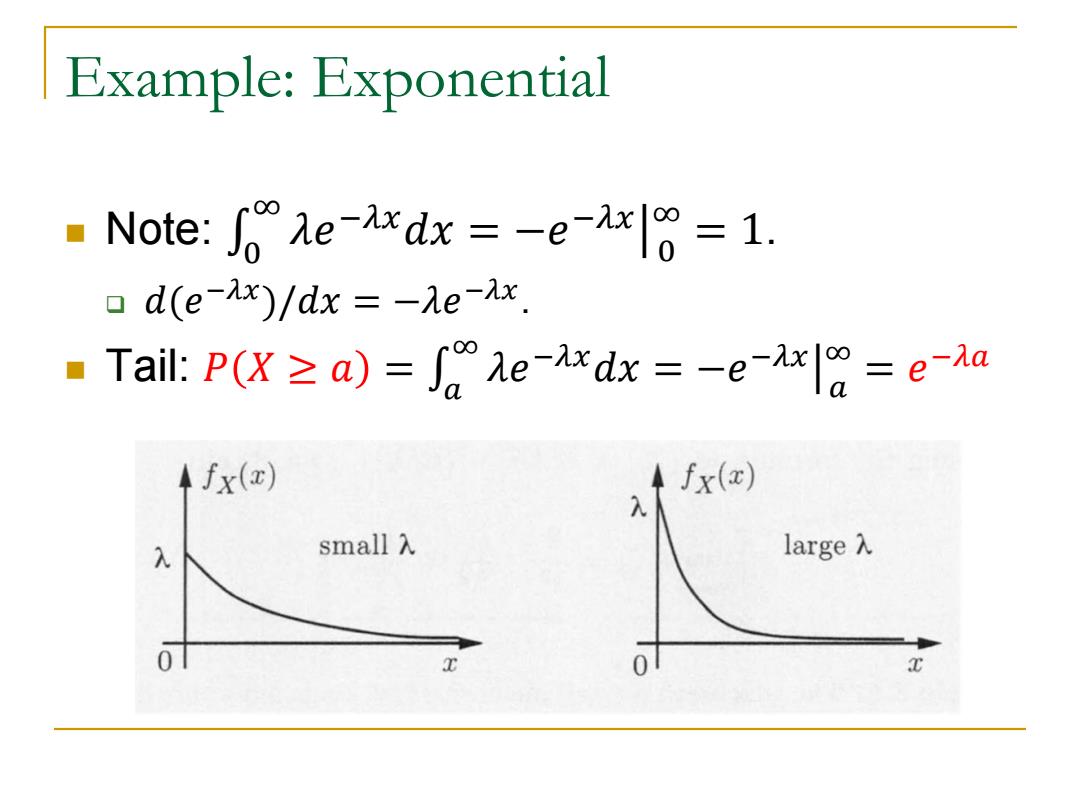
Example: Exponential Note: 𝜆𝑒 −𝜆𝑥𝑑𝑥 ∞ 0 = −𝑒 −𝜆𝑥 ∞ 0 = 1. 𝑑(𝑒 −𝜆𝑥)/𝑑𝑥 = −𝜆𝑒 −𝜆𝑥 . Tail: 𝑃 𝑋 ≥ 𝑎 = 𝜆𝑒 −𝜆𝑥𝑑𝑥 ∞ 𝑎 = −𝑒 −𝜆𝑥 ∞ 𝑎 = 𝑒 −𝜆𝑎

Example:Exponential ■E[X=xhe-Axdx=-xde-x =-xe-ix e +ewt=0 gn 1 元 0 Recall integral by parts:∫udv=uw-∫vdu. ■E[x2]=0x2ne-xdx -e28+ 2 2xe-xdx=E[X]= 2 2 ·Var[X]=E[x2]-E[X]2=1/2
Example: Exponential 𝐄 𝑋 = 𝑥𝜆𝑒 −𝜆𝑥𝑑𝑥 ∞ 0 = − 𝑥 𝑑𝑒 ∞ −𝜆𝑥 0 = −𝑥𝑒 −𝜆𝑥 ∞ 0 + 𝑒 −𝜆𝑥𝑑𝑥 ∞ 0 = 0 − 𝑒 −𝜆𝑥 𝜆 ∞ 0 = 1 𝜆 Recall integral by parts: 𝑢𝑑𝑣 = 𝑢𝑣 − 𝑣𝑑𝑢. 𝐄 𝑋 2 = 𝑥 2𝜆𝑒 −𝜆𝑥𝑑𝑥 ∞ 0 = −𝑥 2𝑒 −𝜆𝑥 ∞ 0 + 2𝑥𝑒−𝜆𝑥𝑑𝑥 ∞ 0 = 2 𝜆 𝐄 𝑋 = 2 𝜆 2 𝐕𝐚𝐫 𝑋 = 𝐄 𝑋 2 − 𝐄 X 𝟐 = 1/𝜆 2

Example Time X of a meteorite first lands in Sahara An exponential r.v.with mean of 10 days. Since E[X]=1/λ,we have=/1o- Question:What's the probability of it first lands in 6am-6pm of the first day? nP(≤X≤)=P(X≥)-P(X≥) 1 3 e 40-e40=0.0476
Example Time 𝑋 of a meteorite first lands in Sahara. An exponential r.v. with mean of 10 days. Since 𝐄 𝑋 = 1/𝜆, we have 𝜆 = 1 10. Question: What’s the probability of it first lands in 6am – 6pm of the first day? 𝑃 1 4 ≤ 𝑋 ≤ 3 4 = 𝑃 𝑋 ≥ 1 4 − 𝑃 𝑋 ≥ 3 4 = 𝑒 − 1 40 − 𝑒 − 3 40 = 0.0476