
A quantum protocol for sampling correlated equilibria unconditionally and without a mediator lordanis Kerenidis,LIAFA,Univ Paris 7,and CNRS Shengyu Zhang,The Chinese University of Hong Kong
A quantum protocol for sampling correlated equilibria unconditionally and without a mediator Iordanis Kerenidis, LIAFA, Univ Paris 7, and CNRS Shengyu Zhang, The Chinese University of Hong Kong

Normal-form games 。k players:P1y,Pk 。P,has a set S;of strategies 。P,has a utility SCISSORS function u:S→R -S=S1×S2×…×Sk strategic(normal)form
Normal-form games strategic (normal) form • k players: P1 , …, Pk • Pi has a set Si of strategies • Pi has a utility function ui : S→ℝ – S = S1 S2 ⋯ Sk
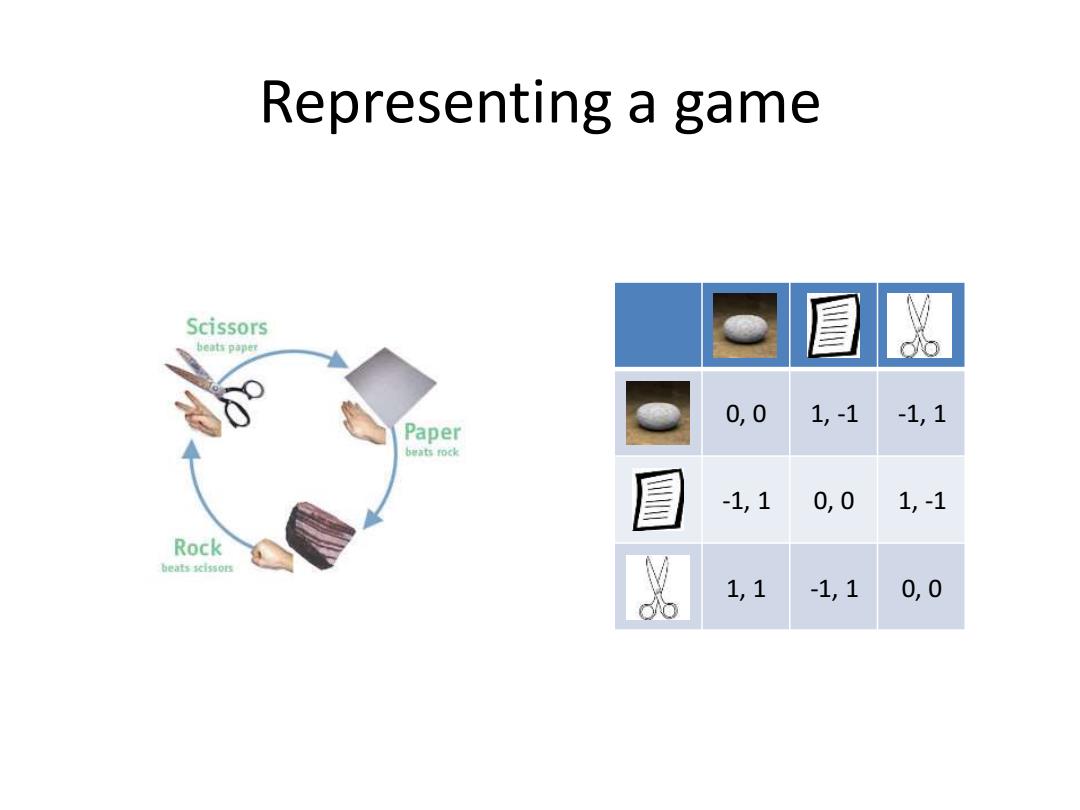
Representing a game Scissors 6eat竹pp 0,0 1,-1-1,1 Paper beats rock -1,1 0,0 1,-1 Rock beats scissors 1,1 -1,1 0,0
Representing a game 0, 0 1, -1 -1, 1 -1, 1 0, 0 1, -1 1, 1 -1, 1 0, 0

Nash equilibrium Nash equilibrium:each player has adopted an optimal strategy,provided that others keep their strategies unchanged
Nash equilibrium • Nash equilibrium: each player has adopted an optimal strategy, provided that others keep their strategies unchanged

Nash equilibrium Pure Nash equilibrium: a joint strategy s=(s1,...,sk)s.t.Vi, u(sS)≥u(SS) -S.1=(S1,,S1-1S41,Si1】 Each Player i can also choose her strategy si randomly,say,from distribution pi. (Mixed)Nash equilibrium (NE): a product distribution p=p1×.×pks.t.i, E5←p[u(ss】≥Es←plu(s5] [VNM44,N51]Any game with a finite set of strategies has an NE
Nash equilibrium • Pure Nash equilibrium: a joint strategy s = (s1 , …, sk ) s.t. i, ui (si ,s-i ) ≥ ui (si ’,s-i ) – s-i = (s1 , …, si-1 , si+1, …, si-1 ) • Each Player i can also choose her strategy si randomly, say, from distribution pi . • (Mixed) Nash equilibrium (NE): a product distribution p = p1 … pk s.t. i, Es←p [ui (si ,s-i )] ≥ Es←p [ui (si ’,s-i )] • [vNM44,N51] Any game with a finite set of strategies has an NE