
Random Walk on Graphs and its Algorithmic Applications Shengyu Zhang Winter School,ITCSC@CUHK,2009
Random Walk on Graphs and its Algorithmic Applications Shengyu Zhang Winter School, ITCSC@CUHK, 2009
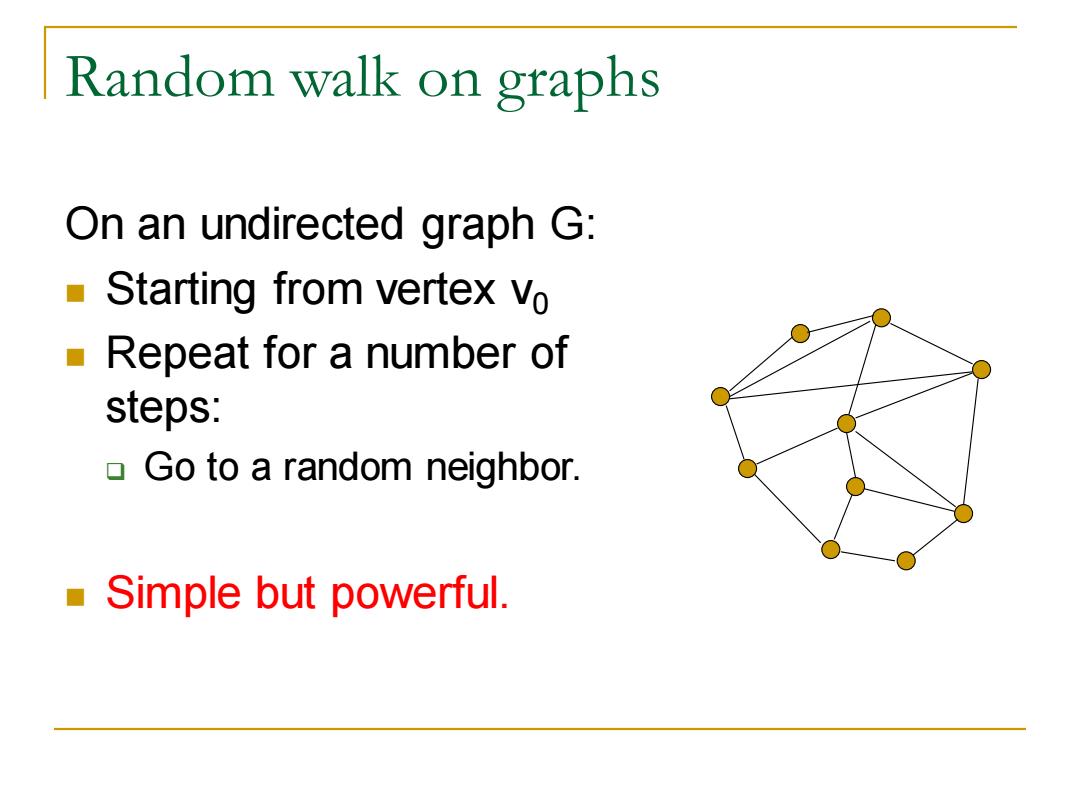
Random walk on graphs On an undirected graph G: ■ Starting from vertex vo Repeat for a number of steps: Go to a random neighbor Simple but powerful
Random walk on graphs On an undirected graph G: ◼ Starting from vertex v0 ◼ Repeat for a number of steps: ❑ Go to a random neighbor. ◼ Simple but powerful

Road map:Random walk Parameters Algorithms /Properties ▣k-SAT Hitting time ▣st-connectivity ▣PageRank Mixing time Approximate counting ▣Error-reduction
Road map: Random walk Parameters /Properties Hitting time Algorithms ❑ k-SAT ❑ st-connectivity Mixing time ❑ PageRank ❑ Approximate counting ❑ Error-reduction
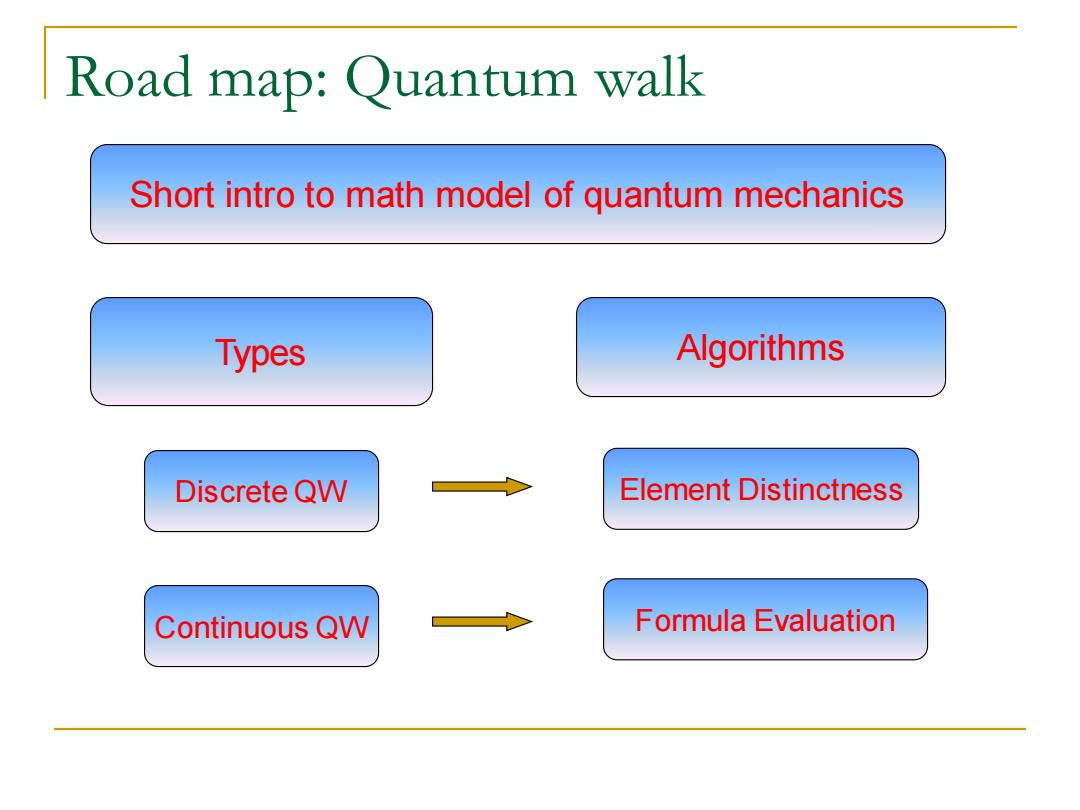
Road map:Quantum walk Short intro to math model of quantum mechanics Types Algorithms Discrete QW Element Distinctness Continuous QW Formula Evaluation
Road map: Quantum walk Types Discrete QW Algorithms Element Distinctness Continuous QW Formula Evaluation Short intro to math model of quantum mechanics

PART I.Random Walk Key parameter 1:Hitting time
PART I. Random Walk Key parameter 1: Hitting time