一、体积功:P外dvW=-lv因系统体积变化而做的功膨胀时:W=-f外dl2= -(f外/A)dl-A=-P外dVp的单位:Pa=N·m2d1PW=-J" p外dvA压缩时W=-Jp外dV显然功的大小与途径有关21
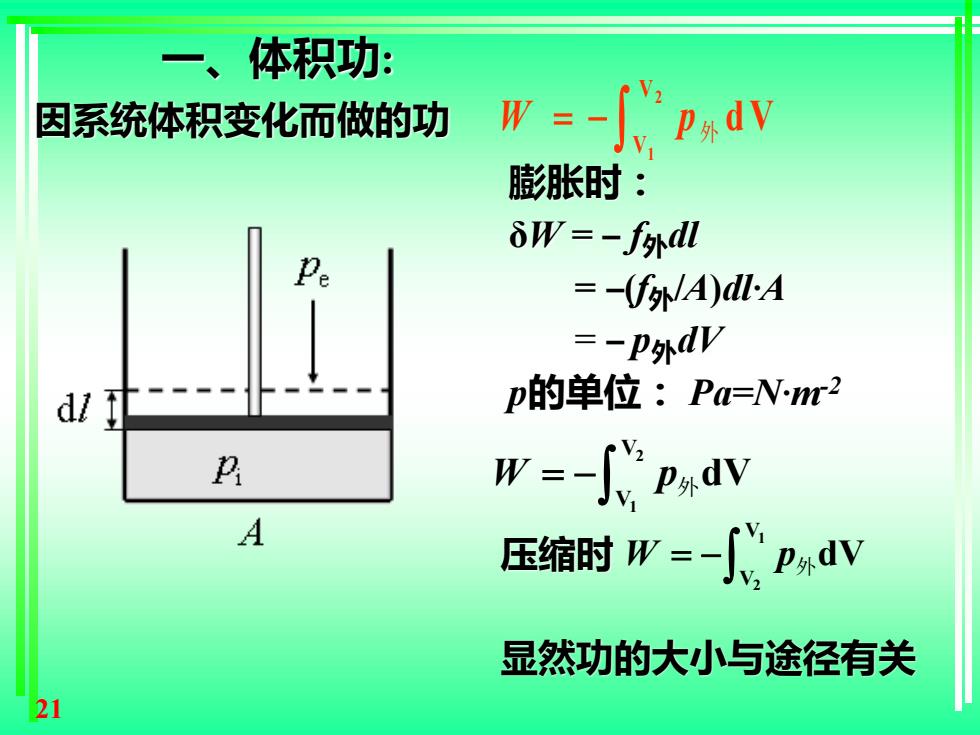
21 一、体积功: 因系统体积变化而做的功 膨胀时: δW = – f外dl = –(f外/A)dl·A = – p外dV p的单位: Pa=N·m-2 显然功的大小与途径有关 压缩时 2 1 V V W p = − 外dV 1 2 V V W p = − 外dV 2 1 V V W p = − d V 外

设在定温下,一定量理想气体在活塞简中克服外压Pe,经4种不同途径,体积从Vi膨胀到V2所作的功。(1)向真空自由膨胀:Wi=0P.=022
22 ⑴向真空自由膨胀: W1=0 设在定温下,一定量理想气体在活塞筒中克 服外压 pe ,经4种不同途径,体积从V1膨胀到 V2所作的功。 pe=0
(2)一次恒外压膨胀所作的功PpVp立Pe=P2VP2VVV阴影面积代表We2W2= - Jp2 dV= - P2(V2-VI)23
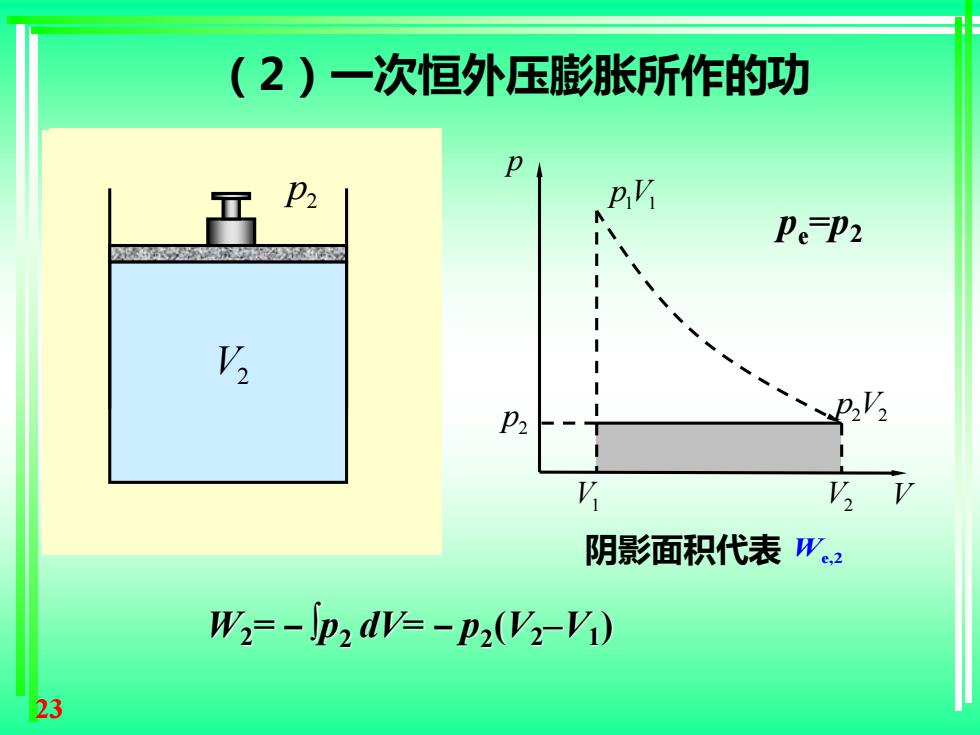
23 V1 1 p pV1 1 p2 V1 V2 V p p V2 2 p2 V1 V2 p2 (2)一次恒外压膨胀所作的功 阴影面积代表 We,2 W2= – ∫p2 dV= – p2 (V2–V1 ) pe =p2
(3)多次等外压膨胀所作的功V膨胀到克服外压为Pe,体积从②克服外压为P2,体积从V月膨胀到V2We, =-p(V'-V)-p,(V, -V)pp,V可见,外压差距越小pi膨胀次数越多,做的功也越多。V1Dpe所作的功等于2次作功pP21的加和。VV224
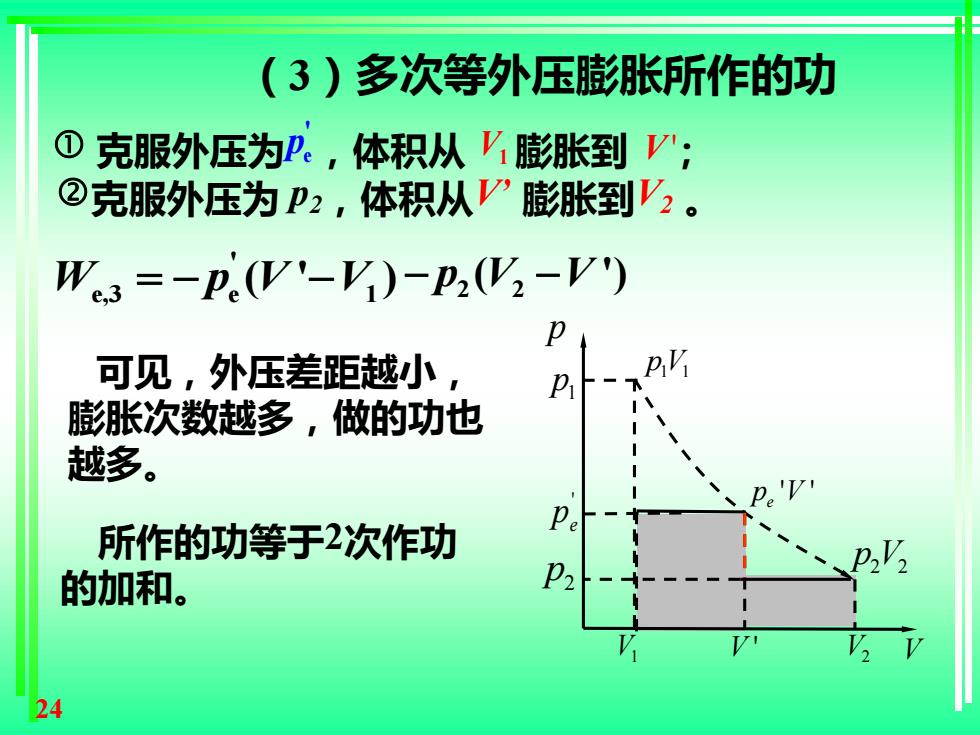
24 可见,外压差距越小, 膨胀次数越多,做的功也 越多。 所作的功等于2次作功 的加和。 1 1 pV V p 2 2 p V 1 p ' e p V ' ' ' e p V 2 p V1 V2 e,3 e 1 ' W p V V = − − ( ' ) 克服外压为 e ,体积从 V1 膨胀到 V ; ' ' p 2 2 − − p V V ( ') 克服外压为 p2,体积从V’ 膨胀到V2 。 (3)多次等外压膨胀所作的功
(4)3外压比内压小一个无穷小的值这样的膨胀过程是无限缓慢的,每一步都接近于平衡态。所作的功为:(p: -dp)dVp.dV=e.4pPVPi4P,dV对理想气体-nRTV2p,VE-nRTIndvP2VVVVV.这种过程系统所作的功最大。阴影面积为W25
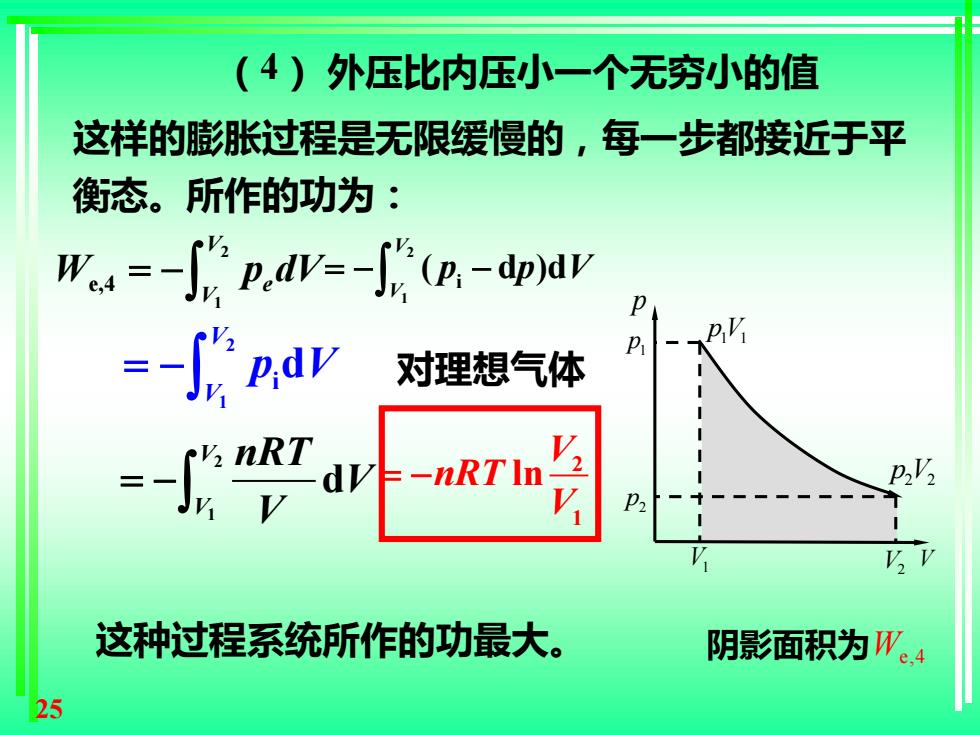
25 (4) 外压比内压小一个无穷小的值 2 1 e,4 V e V W p dV = − 2 1 i d V V = − p V 这样的膨胀过程是无限缓慢的,每一步都接近于平 衡态。所作的功为: 2 1 i ( d )d V V = − − p p V 2 1 lnV nRT V = − 2 1 d V V nRT V V = − 这种过程系统所作的功最大。 对理想气体 V p 1 p V1 p2 V2 2 2 p V 1 1 pV 阴影面积为We,4