
用单位采样序列来表示任意序列 x(n)=∑x(m)8(n-m) m=-o0 δ(n-m)= n =m n≠m
用单位采样序列来表示任意序列 ∑ ∞ =−∞ = − m x(n) x(m)δ (n m) ≠ = − = n m n m n m 0, 1, δ ( )
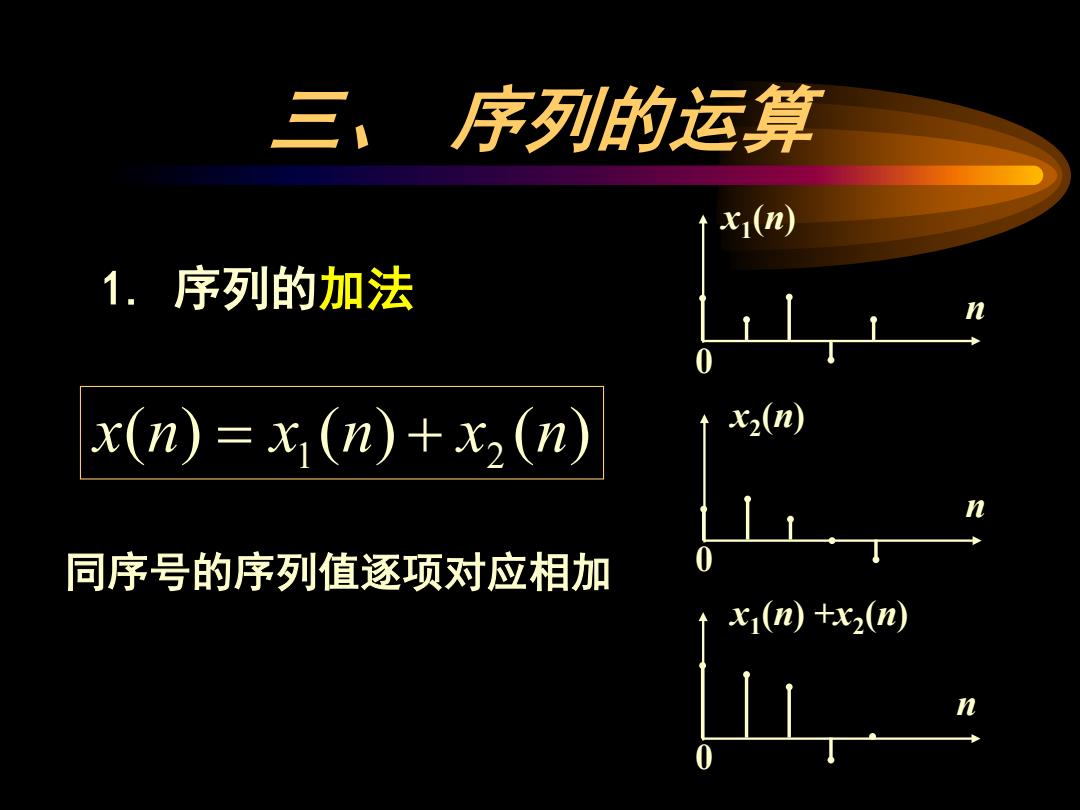
三,序列的运算 x1(n) 1.序列的加法 x(n)=x(n)+x2(n) x2(n) 同序号的序列值逐项对应相加 x(n)+x2(n)
三、 序列的运算 1. 序列的加法 ( ) ( ) ( ) x n = x1 n + x2 n x1(n) n 0 x2(n) n 0 x1(n) +x2(n) n 0 同序号的序列值逐项对应相加
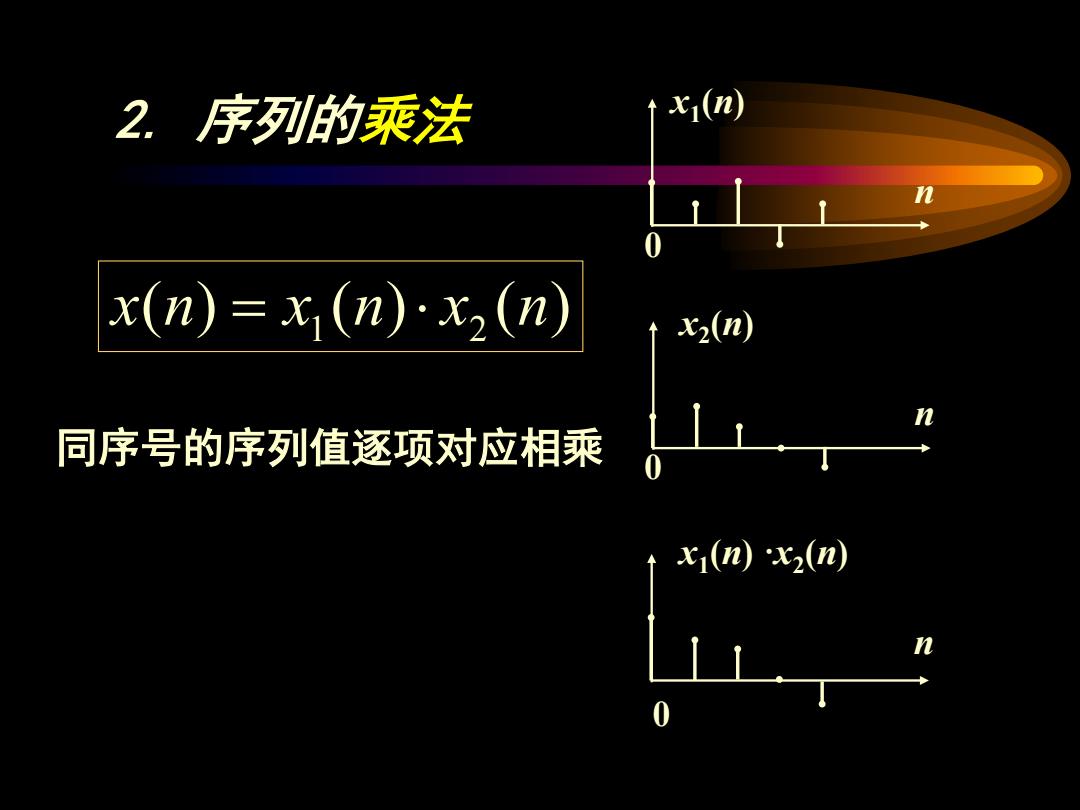
2.序列的乘法 ↑x(n) x(n)=x,(n)x2(n) x2(n) 同序号的序列值逐项对应相乘 x1(n)x2(n) n 0
2. 序列的乘法 ( ) ( ) ( ) 1 2 x n = x n ⋅ x n x1(n) n 0 x2(n) n 0 0 n x1(n) ·x2(n) 同序号的序列值逐项对应相乘
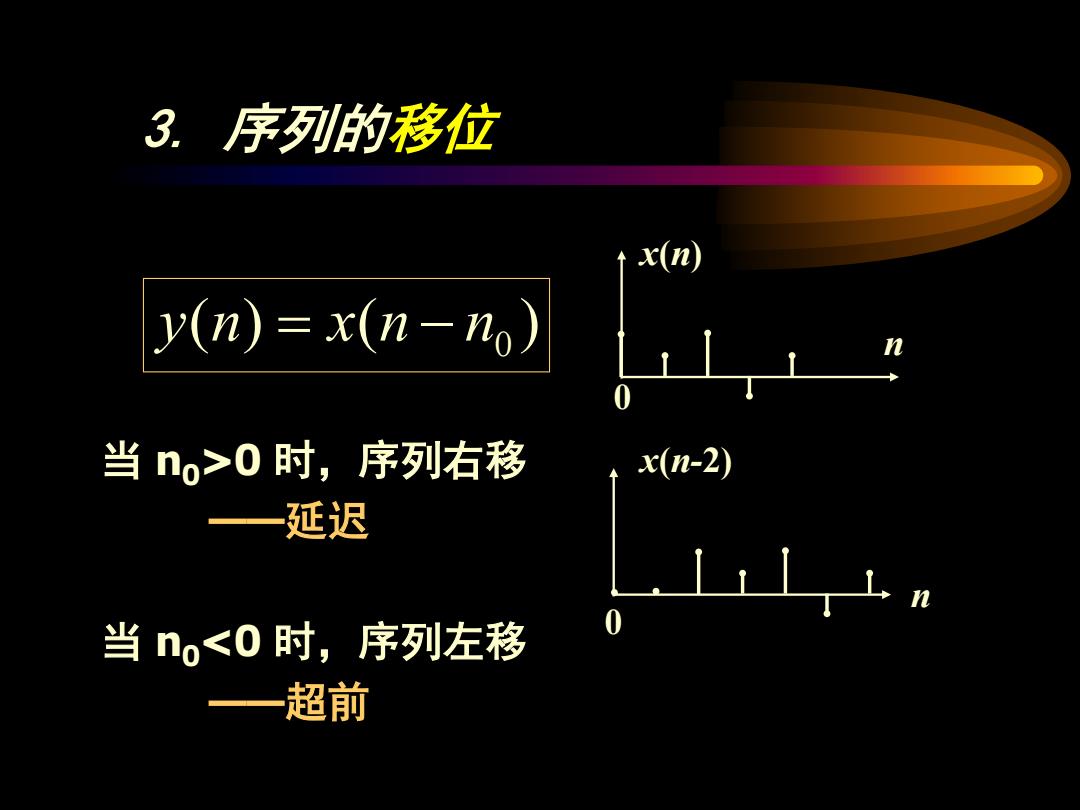
3.序列的移位 x(n) y(n)=x(n-no) 当no>0时,序列右移 ◆x(n-2) 延迟 当no<0时,序列左移 超前
3. 序列的移位 ( ) ( )0 y n = x n − n 当 n0>0 时,序列右移 ——延迟 当 n0<0 时,序列左移 ——超前 x(n) n 0 n 0 x(n-2)

4.序列的翻转 冬x(-n)是x(n)的翻转序列。x(-n)是以纵 轴(n=0)为对称轴将序列x(n)加以翻转。 ↑x(n) x(-n) 0
4. 序列的翻转 n 0 x(-n) x(-n)是x(n)的翻转序列。x(-n)是以纵 轴(n=0)为对称轴将序列x(n)加以翻转。 x(n) n 0