
第一章 离散时对间信号与系统
第一章 离散时间信号与系统

学习目标 掌握序列的概念及其几种典型序列的定义,掌握序 列的基本运算,并会判断序列的周期性。 掌握线性/移不变/因果/稳定的离散时间系统的概 念并会判断,掌握线性移不变系统及其因果性/稳 定性判断的充要条件。 理解常系数线性差分方程及其用迭代法求解单位 抽样响应 了解对连续时间信号的时域抽样,掌握奈奎斯特 抽样定理,了解抽样的恢复过程
学习目标 • 掌握序列的概念及其几种典型序列的定义,掌握序 列的基本运算,并会判断序列的周期性。 • 掌握线性/移不变/因果/稳定的离散时间系统的概 念并会判断,掌握线性移不变系统及其因果性/稳 定性判断的充要条件。 • 理解常系数线性差分方程及其用迭代法求解单位 抽样响应。 • 了解对连续时间信号的时域抽样,掌握奈奎斯特 抽样定理,了解抽样的恢复过程

1.1离散时间信号 一序列 信号是传递信息的函数。针对信号的自变量和函数值的 取值,可分为三种信号: (1)连续时间信号 自变量取连续值,而函数值可连续可离散。当函 数值是连续的,又常称模拟信号,如语音信号、电视信号等。 (2)离散时间信号 自变量取离散值,而函数值连续。 (3) 数字信号 自变量和函数值均取离散值。它是信号幅度离散 化了的离散时间信号
1.1 离散时间信号——序列 信号是传递信息的函数。针对信号的自变量和函数值的 取值,可分为三种信号: (1)连续时间信号 -----自变量取连续值,而函数值可连续可离散。当函 数值是连续的,又常称模拟信号,如语音信号、电视信号等。 (2)离散时间信号 -----自变量取离散值,而函数值连续。 (3)数字信号 -----自变量和函数值均取离散值。它是信号幅度离散 化了的离散时间信号
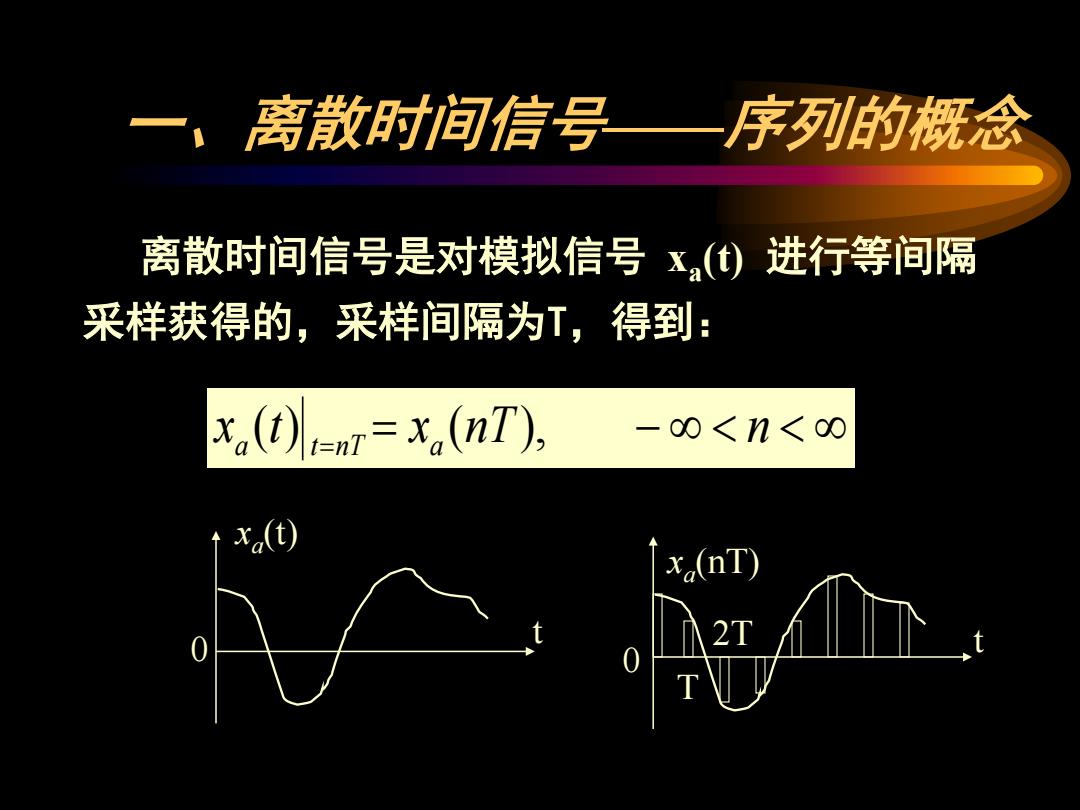
离散时间信号—序列的概念 离散时间信号是对模拟信号x()进行等间隔 采样获得的,采样间隔为T,得到: xa(t)=xa(nT), -0<n<0 x(t) x(nT) 0
离散时间信号是对模拟信号 xa(t) 进行等间隔 采样获得的,采样间隔为T,得到: xa (t) t=nT = xa (nT), − ∞ < n < ∞ 一、离散时间信号——序列的概念 0 t xa(t) 0 xa(nT) t T 2T
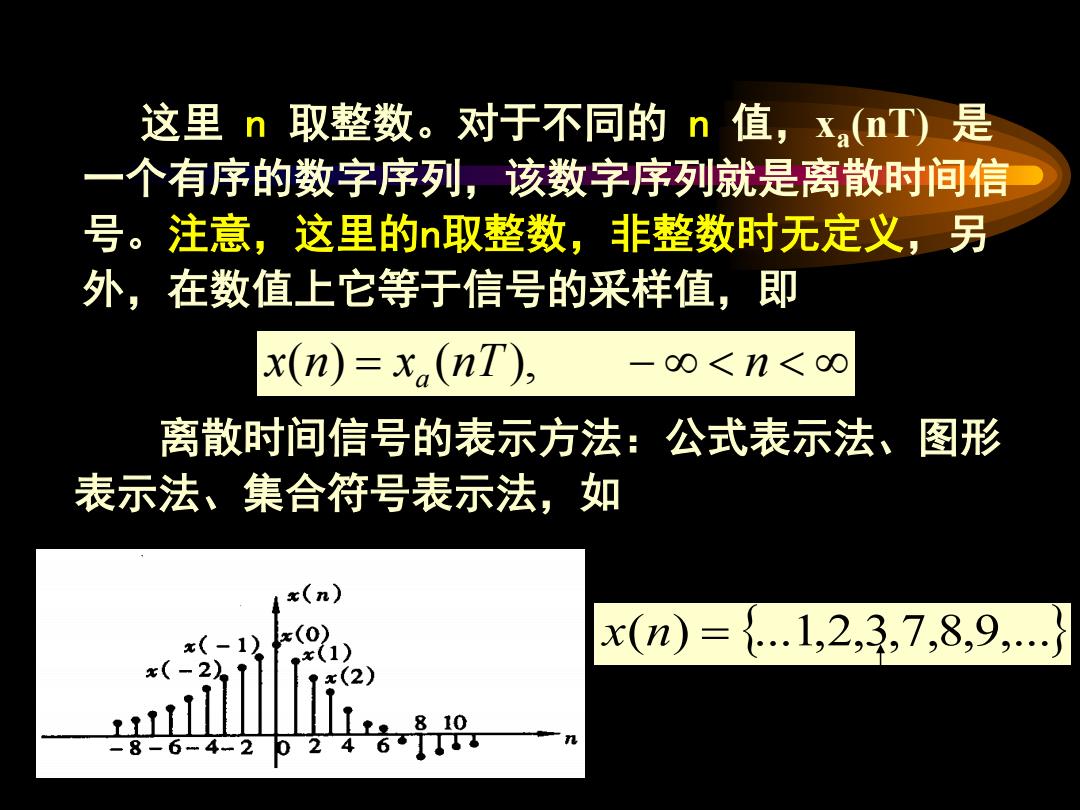
这里n取整数。对于不同的n值,x,(nT)是 一个有序的数字序列,该数字序列就是离散时间信 号。注意,这里的n取整数,非整数时无定义,另 外,在数值上它等于信号的采样值,即 x(n)=x(nT), -0<n<o0 离散时间信号的表示方法:公式表示法、! 图形 表示法、集合符号表示法,如 x(n) x(-1)? x(1) x(n)={1,2,3,7,8,9,…} x(-2) x(2) 1810 8-6-4-2024607
这里 n 取整数。对于不同的 n 值,xa(nT) 是 一个有序的数字序列,该数字序列就是离散时间信 号。注意,这里的n取整数,非整数时无定义,另 外,在数值上它等于信号的采样值,即 x(n) = xa (nT), − ∞ < n < ∞ x(n) = {...1,2,3,7,8,9,...} 离散时间信号的表示方法:公式表示法、图形 表示法、集合符号表示法,如