上海交通大学：《现代控制理论》课程教学资源（讲稿）Chapter 6 Controllability and Observability

Chapter 6 7 Bo Therefore x(0)=-[B AB A"B B The solution of B exists according to initial state x(0)only if following matrix has rank n. rank2c=rank[B7AB。AB A"-B]=n Theory

7 Therefore               1 1 0 1 (0) [ ] n n- β β β x B AB A B     n  rank Q rank[B AB A B A B] 2 n 1 C  The solution of  exists according to initial state x(0) only if following matrix has rank n. Chapter 6

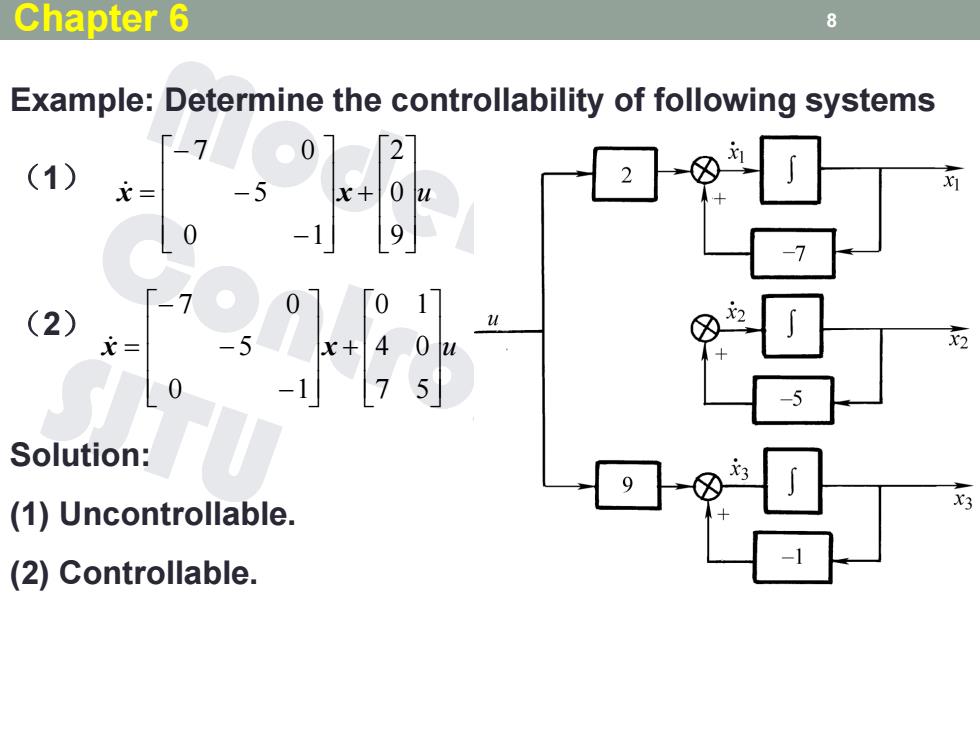
Chapter 6 8 Example:Determine the controllability of following systems 「-7 ●0 2 (1) = 0 2 9 -7 (2) Solution: 9 (1)Uncontrollable. (2)Controllable

8 Example: Determine the controllability of following systems u                          9 0 2 0 1 5 7 0 x x u                          7 5 4 0 0 1 0 1 5 7 0 x x （1） （2） Solution: (1) Uncontrollable. (2) Controllable. Chapter 6

Chapter 6 9 Example:Determine the controllability of following systems -4.1 0 「0 (1) = 0 -4 0 X十 u 0 0 -2 3 -4 0 4 2 0 -4 0 x+ 0 -2 3 。Solution: Theory ·(1)Controllable. ·(2)Uncontrollable

• Example: Determine the controllability of following systems • (1) • (2) 9 u                          3 4 0 0 0 2 0 4 0 4 1 0 x x u                          3 0 0 0 4 2 0 0 2 0 4 0 4 1 0 x x • Solution: • (1) Controllable. • (2) Uncontrollable. Chapter 6

Chapter 6 10 Theorem:If all the eigenvalues of a system are different,then the system can be transformed to the following form using similarity transformation.The system is controllable if there is no all zero row in B. 0 heory

10 Theorem: If all the eigenvalues of a system are different, then the system can be transformed to the following form using similarity transformation. The system is controllable if there is no all zero row in . x x  Bu              n λ λ λ 0 0 2 1   B Chapter 6

Chapter 6 11 Other conditions of controllability Theorem:If a system can be transformed to the following Jordan matrix form using similarity transformation.It is controllable if each row in matrix B corresponding to the last rows of each Jordan block is not all zero row. x+Bu J=

Other conditions of controllability 11 Theorem: If a system can be transformed to the following Jordan matrix form using similarity transformation. It is controllable if each row in matrix corresponding to the last rows of each Jordan block is not all zero row. B Chapter 6 x Bu J J J x               0 k 0 2 1                i i i i λ λ λ 0 1 1 0   J