
Chapter 5 2 Chapter 5 Stability Analysis Objectives: Input-output stability 。Internal stability ·Lyapunov theorem rol Theory Stability analysis of LTI systems
Chapter 5 Stability Analysis Objectives: • Input-output stability • Internal stability • Lyapunov theorem • Stability analysis of LTI systems Chapter 5 2
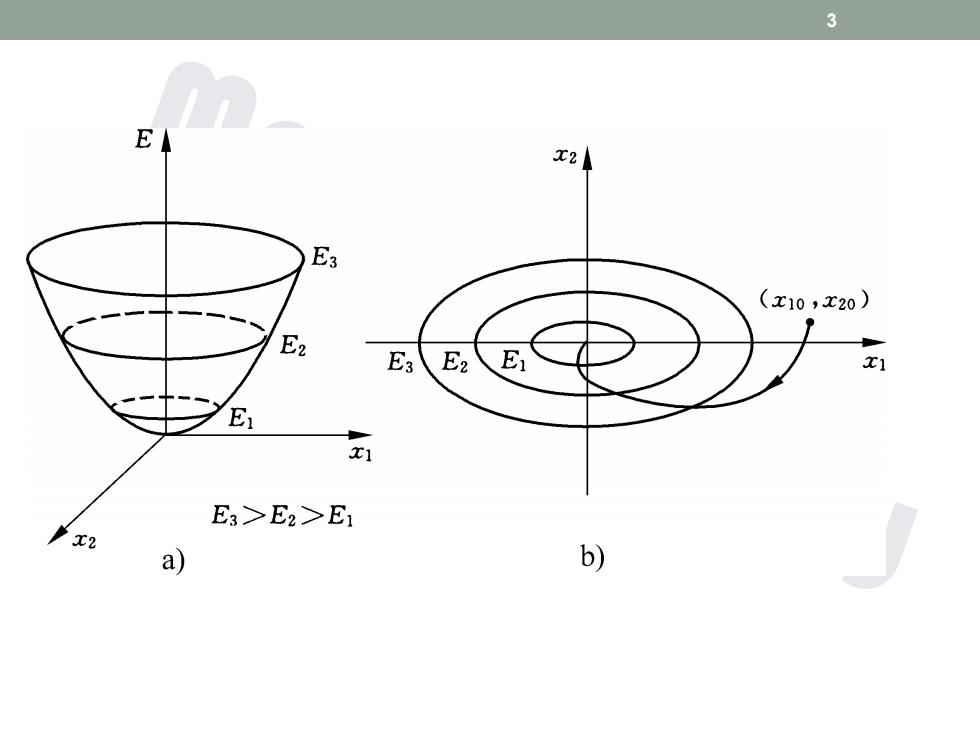
3 E X2 E3 (x10,x20) E2 E3 E2 E x1 E x1 E3>E2>E1 'x2 a) b)
3
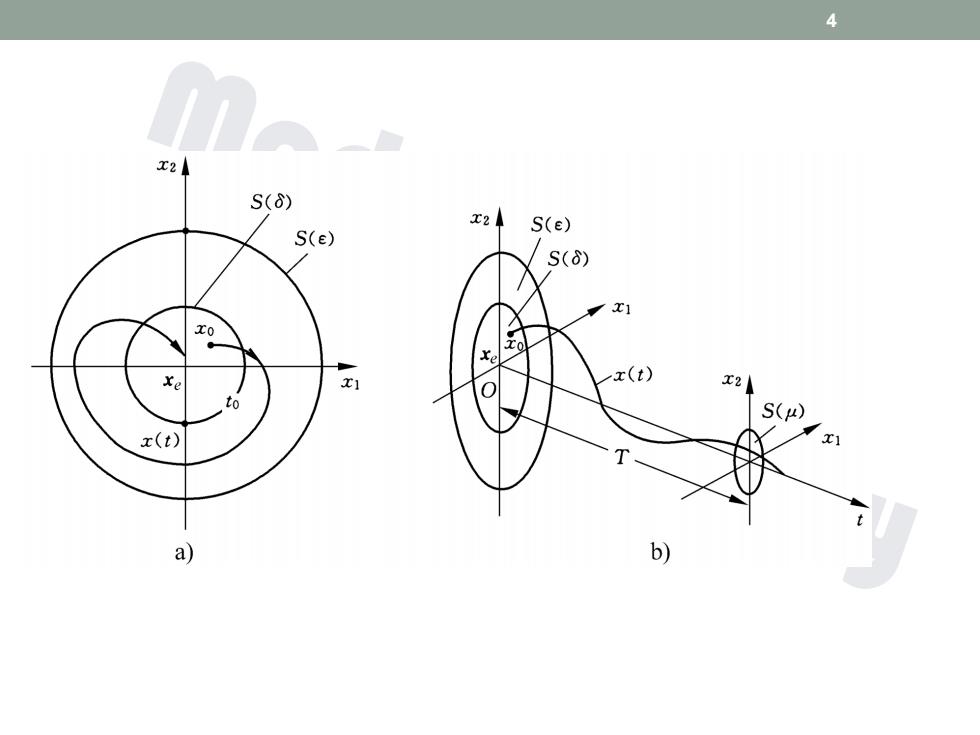
4 S(8) x2 S(e) S(e) S(6) xe x(t) S(μ) z(t) a) b)
4

Chapter 5 5 5.1 Input-output stability An input u(t)is bounded if there exists a constant um: u(t)≤um<oo A system said to be BlBO(bounded input bounded output)if for every bounded input excites a bounded output.The definition is for zero-state response condition or initially relax systems. Theorem:A SISO is BIBO if and only if the pulse response g()is:lg(tdt≤M<o
5.1 Input-output stability • An input u(t) is bounded if there exists a constant um: • A system said to be BIBO (bounded input bounded output) if for every bounded input excites a bounded output. The definition is for zero-state response condition or initially relax systems. • Theorem: A SISO is BIBO if and only if the pulse response g(t) is : 5 u(t ) um g( t )dt M 0 Chapter 5

Chapter 5 6 Proof: If input u is bounded,then< =fst-ww()de ≤lgt-列lur小t=ulst- flgt-dr≤M<o ly≤umM=K2 Therefore,output y is bounded,i.e.K<
Proof: • If input u is bounded, then • Therefore, output y is bounded, i.e. 6 g(t τ) u(τ ) dτ u g(t τ) dτ y g(t τ)u(τ )dτ t t m t t t t 0 0 0 If g(t τ) d τ M t t 0 u M K2 y m u um y K2 Chapter 5