
第3章妆动观点与粒子双点的关系 15 了波列中与最前端相距为五的一点。所以为了使在我们的光谱中能有一条与一定 的动昼对应的锐线[其测不准量由式24)给出],我们必须有-一列长度至少为五的波列, 如果波列太短,我们就没有用到整个光栖.形成光谱的波只是从光搬中很短的扇形区反射 的波,光栅的作用没有很好发挥 一我们将得到一个很大的角展度。为了得到较窄的角展 度,我们必须利用整个光柄,这样至少在某些时刻整个波列应同时从光栅的各部分散射出 来.因此为了使波长的测不准量小于式(2.)所给出的值,波列的长度必须为五.腹便说 袋-4)经 (2.6) 因此 -器 (2.7) 这单乙是波列的长度 这意味着,如果有一长度小于五的波列,那么在波数上的测不准量必然超过2m/工.或 者说波数的测不准量乘以波列的长度 智时我们称之为4 将大于2.我们之所以 称波列长度为4:是因为这是粒子在位置上的测不准量.如果波列只存在于有限长度之中, 那么,这就是我们能找到粒子的区域在测不准量4红范以内.波的这种性质,即波列的长 度乘以相应波数的测不准量至少为2x这一点,是每个研究波的人都知道的,这与量子力学 毫无关系,这只是说,如果我们有一长度有限的波列的话,没有办法很精确地数出波的数 目.我们试从另一途径来看看其中的理由. 假定我们有一长为的有限波列:那么,由于它在两端必定减少(如图2-1所示),所以 在长度五中波的数目是不确定的,其测不雅量为士1,但在长度工中的波数是工/2, 可见声是不确定的,我们又重新得出式(2.7)的结果,它只是波的一种特性.无论波是在空 间传播,是每厘米的弧度数,工是波列的长度,还是波在时间上展开,“是每秒的振动数, T是波列持续的时间“长度”,都会出现同样的情况.这就是说:如果只是持续一定的有限时 间T的波列,那么颜率的测不准量则由下式确定: A6-2/ (2.8) 我们已经着重指出,这些都只是波的性质,例如,在声学理论中就已为人们所熟知了. 要点在于,在量子力学中,我们将波数解释为对粒子动量的一种登度,即卫一,这样 式(2.T)就告诉我们如/4.因此,这就表明了经典动量概念的适用界限.(显然,·如果 我们想用波来表示粒子的话,动量的概念必定受到某种限制!)我们发现了一条规则,使我们 对于经典概念在何时失效具有一些认识,这的确很好。 833晶体衍射 下面,我们考虑粒子波在晶体上的反射.晶体是一块厚厚的东西,它全部由排列得很好 的相同原子组成(我们将在后面包括一些较复杂的情况).问题是对于一束给定的光(区射 线)、电子、中子等等,怎样布置原子的排列才能在某个给定方向上得到强的反射极大值.为 了得到强的反射,来自所有原子的做射都必须是同位相的.同湘波的数量和反相波的数量 不能相等,不然被会相互抵销掉,正如我们已经说明过的那样,解决这个问题的方法是找出 等相位的区域;它们就是一些对入射方向和反射方向成相等角度的平面(图24)
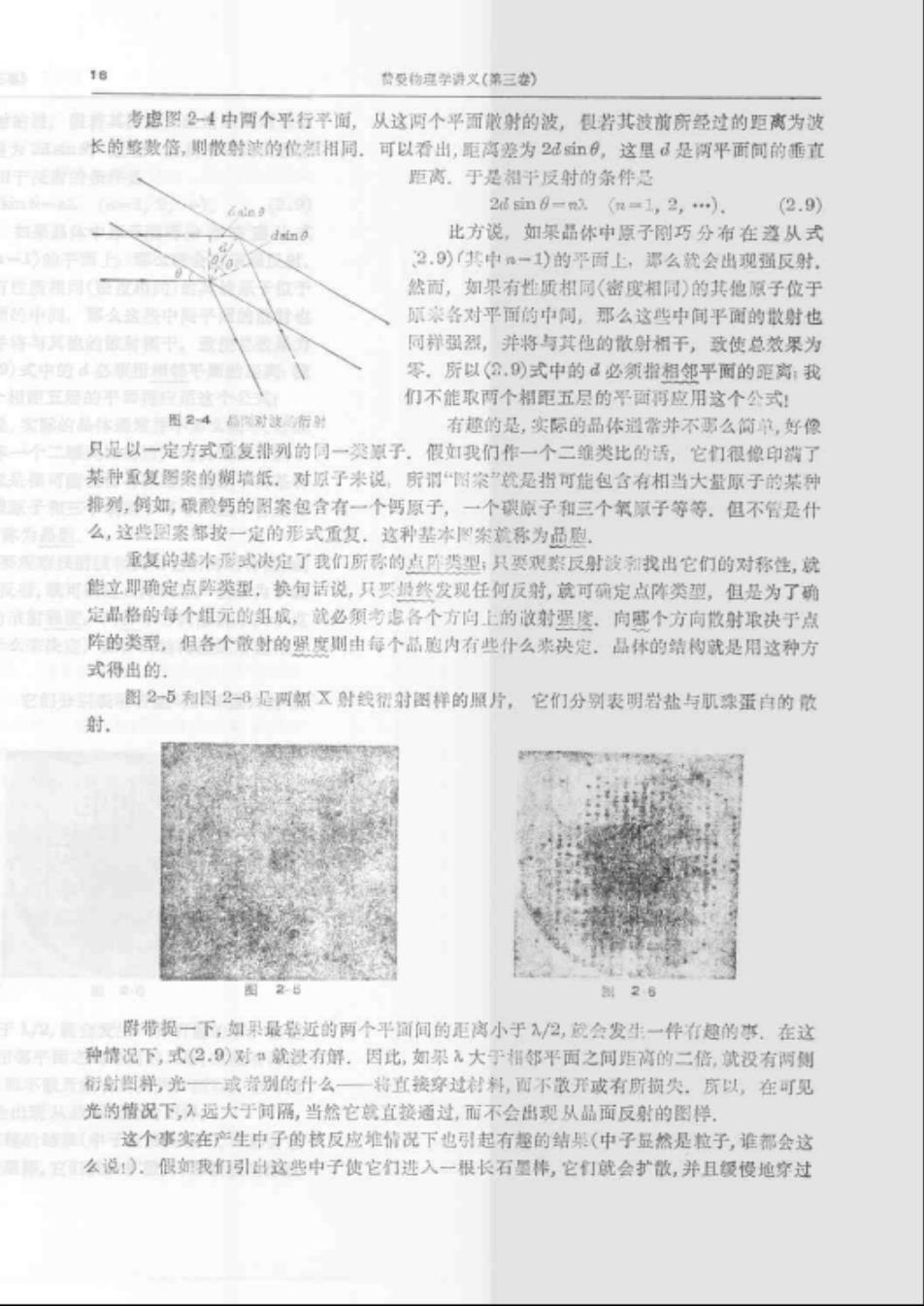
曲受物度学清义(第三) 考虑侧24中两个平行平面,从这阿个平面散射的波,很若其被前所经过的距离为波 长的整数倍,则散射波的位温相同。可以看出,距离差为2品血9,这里是调平面间的垂立 距离.于是相于反时的条件是 m-1,2,… 2.9 比方说,如果品体中原子刚巧分布在透从式 2.9)其中m一1)的平面上,那么就会出现强反射 然面,如果有性质粗同(密度相同)的其他原子位于 各对平面的中间,那么这些中间平面的散射也 同拼强烈,并将与其他的散时相干,政使总效果为 零所以(.)式中的d必须指相平面的距离:我 们不能取两个相距五层的平面再应用这个公式: 图245代发行 有趣的是,实层的品体避常并不男么简单,好偏 只是以一定方式道复排列的同一类漂子.假如虹我们作一个二雏类比的语,它们很像印端了 某种重复图案的墙纸,对子来说所“图案是指可能包含有相当大量原于的某 排列,例如,碳酸钙的图案包合有一个钙原子,一个碳原子和三个氧原子等等.。但不管是什 么,这些园案都按一定的形式质复.这种基木案就称为品胞 重复的基水形式决定了我们所称的点时类型:只要观察反射波和我出它们的对称性,就 能立即确定点阵类型,换句话说,只买域终发现任何反射,就可确定点体类型,但是为了确 定品格的每个组元的组城,就必须考虑各个方向上的微射墨度.向感个方向微时取决于点 阵的类型,组各个散射的强度则由每个品胞内有些什么来决定。品体的结构就是用这种方 式得出的 图2-5和图2-8是网幅X射线帮射图样的照片,它们分别表明岩盐与肌珠蛋白的胸 射 26 附带提一下,如果最铁近的两个平间的正离小于入/2,就会发生一件有避的事.在这 种情况下,式2,)对就没有解。因比,如果元大于相邻平面之间距高的二倍,就没有两侧 衍射四样,光一或普别的什么一将直接穿过料,四不散开成有所损失。京以,在可见 光的情况下,入远大于隔,当然它统直接通过,丽不会出现从品面反射的图样 这个事实在产生中子的枝反应堆情况下也引起有趣的结果(中子显然是粒子,谁都会这 么说).假如我们引白这些中子使它们进入一根长石题棒,它们就会扩散,并且缓侵地穿过

第2章被动观点与粒子观点的关系 17 强度 中子禄三 石卧 二长x申子 短入中子 图2-7反应堆中子通过石熟块扩散 图2-8从石强棒出来的中子强度鸟波长的关系 石墨棒(图2),它们之所以扩散是因为被原子弹开,但严格地说,按照波动理论,它们之 所以被原子弹开是由于晶面的衍射.结果表明,假如我们取一根长石墨棒的话,从远端跑出 的中子都具有长的波长!事实上,假如我们把中子强度作为波长的函数作图的话,只有在波 长大子某个极小值时才出现曲线(图2-8),换句活说,我们可以用这种方法得到校慢的中子 只有最慢的中子才会通过;它们没有被石墨棒的晶面所衍射或散射,而是像光线通过玻璃 样径直穿过石恐棒,没有向两边散射,出去.还有许多其他证据也说明中子波和别的粒子波 是真实的 §24原子的大小 现在我们来看一下由式(23)所表示的测不准关系的另一个应用.在这里不用过分认 真;概念是正确的,但所作的分析并不很精确。这个概念涉及到确定原子的大小,以及按经 典说法,电子将不断辄射出光,因而一直作螺旋运动,直至最后落到原子核上这一事实,但 是这种说法不符合量子力学的观点,因为那样一来我们就同时知道每一个电子的所在以及 它运动得有多快。 假定我们有一个氢原子,现在要测登电子的位登;我们肯定不能精种地预言电子的位 置,不然动量的扩散将会达到无限大。每当我们视察电子时,它是在某处,但是它在各个不 同地方都有一定的振幅,因而在那些地方都可能找到它.这些位置不可能全都在原子核处, 我们将假定位置有一定的扩展,其大小纳为6,这就是说,电子离原子核的距离通常约为@ 我们将由原子的总能量取极小值这个条件来确定4的数值。 由于测不准关系,劲量的散布约为/@,这样,如采我们打算用某种方式去测量电子的 动量,譬如使它散射X射线,然后寻找运动散射体的多普勒效应,那么可以预期并不会每 次都得到零一一电子并不是静止不动的一但它的动量一定约为p≈/,于是动能约为 1/2mv2=/2m一/2m心2.(在某种意义上,这是一种量纲分析,用以找出动能是以何种方 式取决于普朗克常数,质量m,以及原子的大小a.我们毋需两虑答案中2m等这类因子上 的出入,事实上,我们甚至还没有很精确地定义过4.)现在,势能为一€除以离原子中心的 距离,即一e/a,这里的e大家记得就是电子电荷的平方除以4r0.要点就在于,如果a变 小,势能就变小,但越小,由于测不准关系,所需的动:也就越大,因而动能也越大.总能 量是 (2.10) 我们不知道a究凳为多大,但我们却知道原子本身会进行安排,以取得某种折衷办法使能爱 尽可能地小.为使E保持极小,我们求公对a的微商,令此微商等于零后再解出a,亚的 徽商是

18 费受物理学讲义(邻三卷) 器+ (2.11) 令票-0,求得4值为 6--0.528埃-0.528×10-0米 (2.12) 这一个特殊的距离称为波尔半经.我们因此得知原子的大小约为埃的数量级,这个结论是 正确的:这是一件挺不错的事一实际上,这是一件令人惊奇的事,因为在这以前,我们还没 有推断原子大小的根据:从经典的观点来看,由于电子会螺旋式地落到原子核上,原于完全 不可能存在. 现在,如果将(2.12)的%值代入(2.10)去求能是,结果得出 私-一云-器一186电子伏特 (2.13) 能贤为负意珠者什么?这意味着,当电子在原子中时的能量比自由状态下的能量小.这就是 说,它是受束缚的.也就是说,要把电子“踢出去”需要能是:要电离一个氢原子大约需要 13.6电子伏特的能量。我们没有理由认为所需的能量不是这个值的2倍、3倍或专倍、 (伯))倍,因为我们这里所用的是十分起略的论正。然面,我们在这里悄悄地这样来使用所有 的常数,使得正好得出正确的数字!13.6电子伏特这个数学称为一个里德伯(Bydg)能 量,它是氢原子的电离能。 所以,我们现在懂得了为什么不会掉到地板下面去.当我们行走时,鞋子中的大量原子 推斥着地板中的大量原子.为了把原子挤得更靠近一些,电子必须被限制在一个较小的空 间,由测不准关系,平均而言它们的动盘将变得大些,这就卷味着能量变大:抵抗原子压缩的 是一种量子力学效应,面不是经典效应.按照经典的观点,如果使所有电子与质子更为靠 近,我们应预拥能量会进一步降低,因此,在经奥物学中,正电荷与负电荷的最佳排列就是 互相紧靠在一起.这些在经典物理学中是很清楚的,但是由子原子的存在又令人困惑.当 然,早先的科学家发明过一些办法来摆脱这个困境 一不过别去管它,我们现在找到了一种 正确的方法!(也许如此.) 顺便提一下(虽然眼下我们还不具备理解它的基础),在有许多电子的场合中,这些电子 总是试图彼此离开,如果某个电子正占据者某一空间,那么另一个电子就不会占据同一空 闻。说得更精确一些,由于存在者两种自旋的情况,因此两个电子有可能紧靠在一起,一个 电子沿一个方向自旋,而另一个电子则沿反方向自能.但此后我们在该处再也不能放进更 多的电子.我们必须把其他电子放到别的位置上,这就是物质具有强度的真正原因.·假如 我们有可能将所有电于放在同一个地方,那么它们将会比现在更为凝菜.正是由于电子不 可能全都紧靠在一起这个事实,才使得桌子和其他种种东西变得坚固, 十分明显,为了理解物质的性质,我们必须用量子力学,经典力学在这方面是不会令人 满意的。 825能 级 我们已讲过处在可熊具有的最低能量状态下的原于,但是结果丧明电子可以具有别种

第3章收动现点与粒子观点的关系 19 状态,它能以更有力的方式旋转与振动,因此原子可以有多种不同的运动.按照量子力学, 在稳定状态下,原子只可能有确定的能量.我们作了一个图(图29),其中垂直方向标绘能 最,每一个允许的指最值面一条水平线当电子是自由电 子,即它的能量为正时,它可以具有任何值,并能以任何速 率运动.但是束细能不能取任意值.原子必须取如图2-9 所示的一组允许值中的某一个能量。 现在我们称这些能量的允许值为E。,E,正,E,如 果原子本来处于E,卫,等“激发态”之一时,它不会永远保 图2-9原千的能级图(表 取这种状态.迟早它会掉到较低的状态中去,并以光的形 示是种可能的跃迁) 式辐射出能量.发射出的光的颜率可由能量守恒关系加上量子力学的一个关系式[即光的 频率与光的能量之间的关系式(2.1)]来确定.因此,警如说从能量E到能量E:的跃迁所 释放的光的频率即为 w1=(3一E)/先 (2.14) 于是,这就是原子的一个符征频率,它确定了一条发射谱线.另一种可能跃迁是从E:至可, 这时就有一个不同的频常 w0-(-E)/h. (2.15) 另一个可能性是,如果原子已被激发到E1态,它可能掉回到基态卫,而发射出的光子的频 率是 0HD=(E生mE。)/侨 (2.16) 我们举出三种跃迁的情况是为了指出一个有超的关系.由式(2.14),(2.1和(2.16)很容 易看出 00=1十10. (2.17 一般来说,如果我们找到了两条谱线,可以预期在颁率之和(或之差)处将找到另一条谱线, 而且通过找到这样一系列能,使每条谱线对应于其中的某一对能级的能量差,那么所有的 谱线就能得到理解.在量子力学出现以前人们就已注意到这种在谱线频宗上出乎意外的巧 合,它称为里兹()里合原则,从经典的观点来酒,这又是不可思议的.不过,我们别再 唠明经典力学在原子领域中的尖救,看来我们已讲得很够了. 前面已经谈到量子力学可以用振幅来阐述,振幅的行为很像波,它们具有一定的颜率和 被数。让我们看下,从振辐的观点怎样会得出原子具有确定的能登状态.从我们至今所 说过的那些事楷出发是无法理解这一点的,但是我们都知道被限制的波具有确定的频串,例 如,若声音限制在一个风琴管或任何类似的东西中时,声凌振动的方式就不止一种,但对每 种方式都有一个确定的期率.这样,将波限制在其中的物体有某些确定的谐振频率 所以 这是被限制在一定空间中的波的一个性质一一这个课题我们将在以后详细地用公式来讨沦 这些波只能具有一些确定的颜率.由于振幅的频率与能量间存在着一般关系,我们发 现束缚在原子内的电子其有确定的能最就不足为奇了, 826哲学含义 我们简单地谈谈贷子力学的某些哲学含义.通常问恶总是有两个方面:一个是对于物 理学的哲学含义,另一个是把哲学上的问题外推到其他氧域。在把跟科学相联系的哲学观