
过渡系元素的磁性 磁性 磁矩的计算 √纯自旋磁矩 √轨道磁性对磁矩的贡献 √旋一轨偶合对磁性的影响
过渡系元素的磁性 ✓ 磁性 ✓ 磁矩的计算 ✓ 纯自旋磁矩 ✓ 轨道磁性对磁矩的贡献 ✓ 旋-轨偶合对磁性的影响
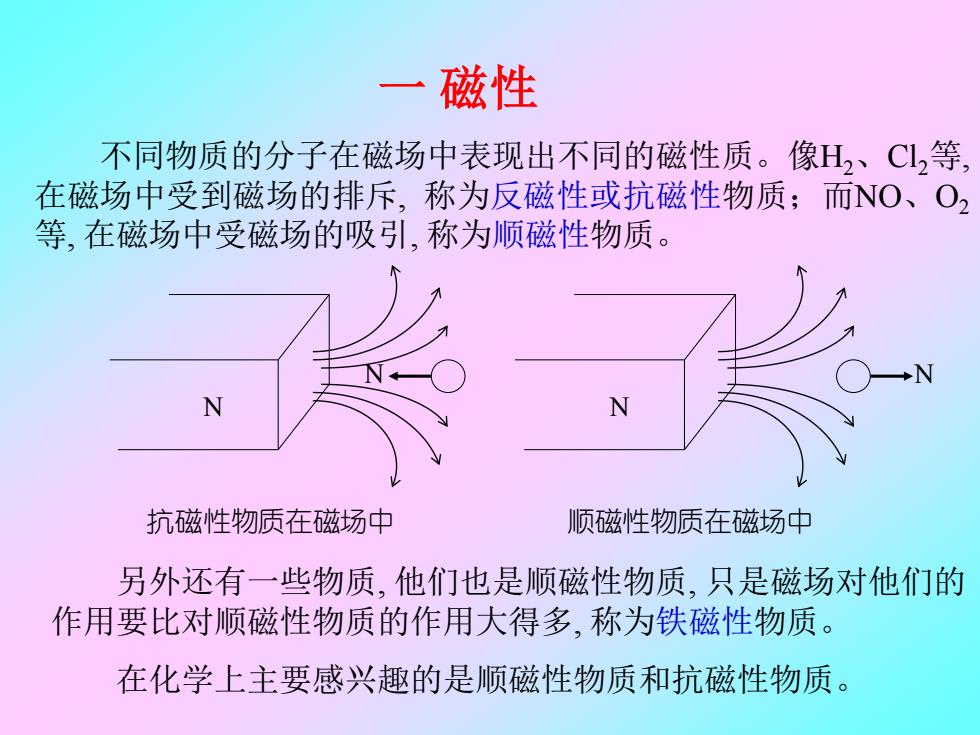
一磁性 不同物质的分子在磁场中表现出不同的磁性质。像H2、C,等, 在磁场中受到磁场的排斥,称为反磁性或抗磁性物质;而O、O2 等,在磁场中受磁场的吸引,称为顺磁性物质。 N N 抗磁性物质在磁场中 顺磁性物质在磁场中 另外还有一些物质,他们也是顺磁性物质,只是磁场对他们的 作用要比对顺磁性物质的作用大得多,称为铁磁性物质。 在化学上主要感兴趣的是顺磁性物质和抗磁性物质
一 磁性 不同物质的分子在磁场中表现出不同的磁性质。像H2、Cl2等, 在磁场中受到磁场的排斥, 称为反磁性或抗磁性物质;而NO、O2 等, 在磁场中受磁场的吸引, 称为顺磁性物质。 N N 抗磁性物质在磁场中 N N 顺磁性物质在磁场中 另外还有一些物质, 他们也是顺磁性物质, 只是磁场对他们的 作用要比对顺磁性物质的作用大得多, 称为铁磁性物质。 在化学上主要感兴趣的是顺磁性物质和抗磁性物质

分子中的电子在绕核的轨道运动和电子本身的自旋运动都 会产生磁效应。电子自旋运动产生自旋角动量,从而产生自旋 磁矩;电子的轨道运动产生的轨道角动量,产生轨道磁矩。当 把分子作为一个整体看时,构成分子的各个电子对外界产生的 磁效应的总和可用一个等效的环电流(称为分子电流)表示,这 个环电流具有一定的磁矩,称为分子磁矩。在多数情况下,分 子磁矩主要是由电子自旋产生的。如果物质的原子或分子轨道 中,所有的电子都已配对,那么由配对的电子的自旋产生的小 磁场两两大小相等、方向相反,磁效应互相抵消,净磁场等于0, 若将这种物质放在外磁场中,在其作用下,就要产生一个与外 磁场方向相反的诱导磁矩而受到外磁场的排斥,因此,没有未 成对电子的原子、分子或离子都具有抗磁性;如果物质具有未 成对电子,则由单电子的自旋产生的小磁场不能被抵消,净磁 场不等于0,则该物质具有顺磁性,这种物质在外磁场中,不仅 产生一个与外磁场方向相反的诱导磁矩,而且它的分子磁矩还 沿磁场方向取向,由于分子磁矩比诱导磁矩要大得多,总的结 果是产生了与磁场方向一致的磁矩,因而受到外磁场的吸引, 因此,具有未成对电子的物质大都具有顺磁性
分子中的电子在绕核的轨道运动和电子本身的自旋运动都 会产生磁效应。电子自旋运动产生自旋角动量, 从而产生自旋 磁矩;电子的轨道运动产生的轨道角动量, 产生轨道磁矩。当 把分子作为一个整体看时, 构成分子的各个电子对外界产生的 磁效应的总和可用一个等效的环电流(称为分子电流)表示, 这 个环电流具有一定的磁矩, 称为分子磁矩。在多数情况下, 分 子磁矩主要是由电子自旋产生的。如果物质的原子或分子轨道 中, 所有的电子都已配对, 那么由配对的电子的自旋产生的小 磁场两两大小相等、方向相反, 磁效应互相抵消, 净磁场等于0, 若将这种物质放在外磁场中, 在其作用下, 就要产生一个与外 磁场方向相反的诱导磁矩而受到外磁场的排斥, 因此, 没有未 成对电子的原子、分子或离子都具有抗磁性;如果物质具有未 成对电子, 则由单电子的自旋产生的小磁场不能被抵消, 净磁 场不等于0, 则该物质具有顺磁性, 这种物质在外磁场中, 不仅 产生一个与外磁场方向相反的诱导磁矩, 而且它的分子磁矩还 沿磁场方向取向, 由于分子磁矩比诱导磁矩要大得多, 总的结 果是产生了与磁场方向一致的磁矩, 因而受到外磁场的吸引, 因此, 具有未成对电子的物质大都具有顺磁性

二兹矩的计算 (一)纯自旋磁矩 在多数情况下,分子磁矩主要是由电子的自旋产生的,纯的 自旋磁矩可根据总自旋量子数进行计算。 Hs=g/S(S+1) 其中$为总自旋量子数,等于未成对电子数的一半,g为朗德 因子,对于自由电子,g=2.0023,通常取g=2,于是上式变为: u三√n(n+2) 式中为未成对电子数。这个式子表明,如果忽略了轨道角 动量对磁矩的贡献,可由磁矩直接计算出某种离子的未成对电 子数。 按这个公式算出来的磁矩,在少数情况下与实验值不一致, 这正是由于忽略了未成对电子的轨道运动对磁矩的贡献之故
二 磁矩的计算 (一) 纯自旋磁矩 在多数情况下, 分子磁矩主要是由电子的自旋产生的, 纯的 自旋磁矩可根据总自旋量子数进行计算。 s =g 其中S为总自旋量子数, 等于未成对电子数的一半, g为朗德 因子, 对于自由电子, g=2.0023, 通常取g=2, 于是上式变为: s = 式中n为未成对电子数。这个式子表明, 如果忽略了轨道角 动量对磁矩的贡献, 可由磁矩直接计算出某种离子的未成对电 子数。 按这个公式算出来的磁矩, 在少数情况下与实验值不一致, 这正是由于忽略了未成对电子的轨道运动对磁矩的贡献之故。 n(n + 2) S(S+1)

(二)轨道磁性对磁矩的贡献 如果加上轨道磁性对磁矩的贡献,则磁矩的计算公式变为: us+L=V4S(S+1)+L(L+1) 按照这个公式计算出来的磁矩在大多数情况下也与实验值 不一致。表明在多数情况下,轨道角动量对分子磁矩的贡献很 小或没有贡献。 研究表明:轨道角动量对分子磁矩是否有贡献取决 于外磁场改变时电子能否自旋平行地在不同轨道之间 再分配。这种分配必须在对称性相同的能级之间进行
(二) 轨道磁性对磁矩的贡献 如果加上轨道磁性对磁矩的贡献,则磁矩的计算公式变为: S+L = 4S(S+1) +L(L+1) 研究表明:轨道角动量对分子磁矩是否有贡献, 取决 于外磁场改变时电子能否自旋平行地在不同轨道之间 再分配。这种分配必须在对称性相同的能级之间进行。 按照这个公式计算出来的磁矩在大多数情况下也与实验值 不一致。表明在多数情况下, 轨道角动量对分子磁矩的贡献很 小或没有贡献