
导波场论 STC 回顾电磁场边界条件推导 高等数学中的高斯定律 2:=2(x,y) ∬7.Adw=∬nAds Σ1:2=2(x,) 其中n为包围体积V的封闭面S的外法向矢量 →j∬V×Ad=nx Ads V(C×A)=A(×C)-C(7×A) V(C×)=-C(×A) 麦氏四个微分方程(时谐电磁场): V×E=-jouH 7×H=(j0e+o)E=j08E+J 7.D=P V.B=0
导 波 场 论 回顾 电磁场边界条件推导 高等数学中的高斯定律 V S v s Adv n Ads n 其中 为包围体积 的封闭面 的外法向矢量 v s Adv n Ads C A C A C A A C C A 麦氏四个微分方程(时谐电磁场): H 0 j j j E H E E J D B

导波场论 回顾电磁场边界条件推导 j∬VxEdv=--jojμiHdw VxH=jofeEd+旷.Jd 1区 j∬.Dw=∬pd 2区 §-n ∬V.Bar=0 xEds--joJSS.uHdy ∬7×Aw=∬nxAd nkHds=jFdy+dv 川iAh=前nAds nDsc,陕包围高斯盒 Bds-0 面积的外法向
导 波 场 论 1区 2区 S=n n S=-n E H H E J D B 0 v v v v v v v v dv j dv dv j dv dv dv dv dv v s Adv n Ads E H H E J D B 0 s v s v v s v s n ds j dv n ds j dv dv n ds dv n ds 为包围高斯盒 面积的外法向 v s Adv n Ads 回顾 电磁场边界条件推导
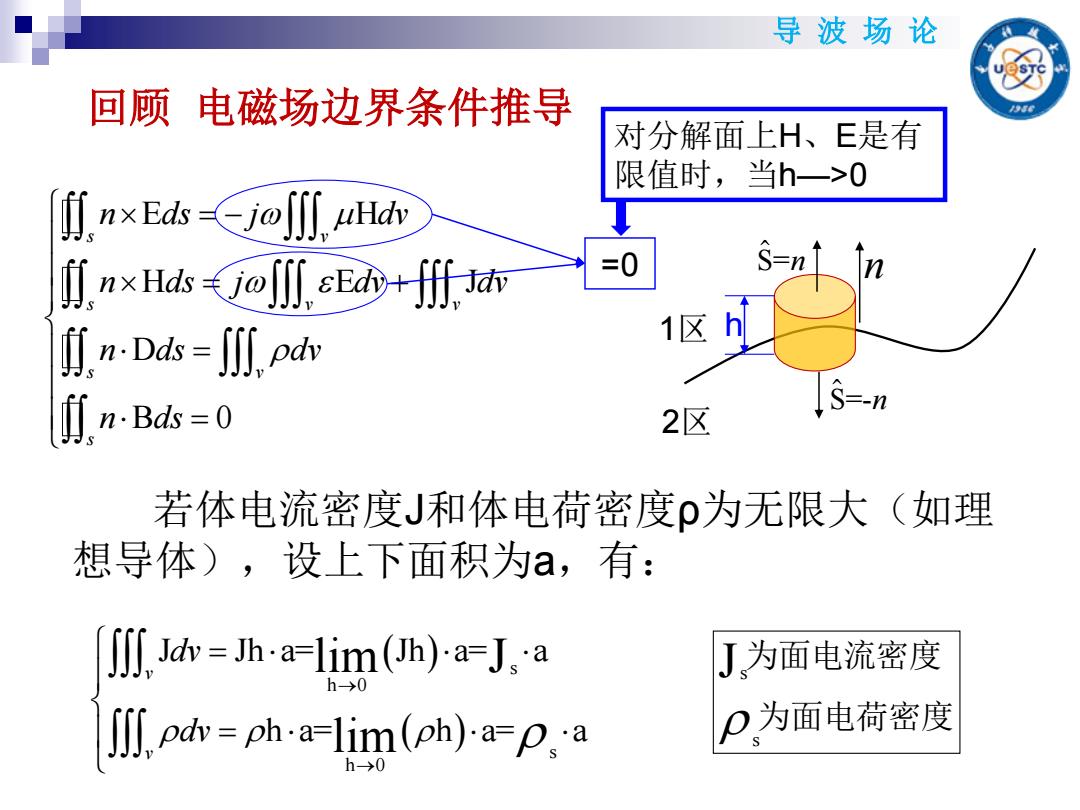
导波场论 回顾电磁场边界条件推导 对分解面上H、E是有 限值时,当h一>0 nxEds -jo uHdv nxHds-jo∬sE+fft =0 S=n1 In fin-Dds=J∬npd 1区h n.Bds=0 S=-n 2区 若体电流密度J和体电荷密度ρ为无限大(如理 想导体),设上下面积为a,有: Jdy=Jh-a-lim(Jh)a=J.a J为面电流密度 h-→0 Ipdy=ph.a=lim(ph)apa P为面电荷密度 10
导 波 场 论 1区 2区 S=n n S=-n h 对分解面上H、E是有 限值时,当h—>0 E H H E J D B 0 s v s v v s v s n ds j dv n ds j dv dv n ds dv n ds =0 若体电流密度J和体电荷密度ρ为无限大(如理 想导体),设上下面积为a,有: s h 0 s h 0 J Jh a= Jh a= a h a= h a= a lim J lim v v dv dv s s J 为面电流密度 为面电荷密度 回顾 电磁场边界条件推导

导波场论 回顾电磁场边界条件推导 有: ∬nxEds=0 J为面电流密度 nxHds=J,a p为面电荷密度 1区 川nDdk=p,a S=-n n.Bds=0 2区 对面积分,h一>0时, nx(E-E2)=0 忽略在小高斯盒侧面的 nx(H-H2)=J, 积分,两边消除a,有: n(D-D2)=Ps n(B,-B2)=0 电磁边界条件的数学关系是由麦克斯韦方程推导而得 根据实际场景,按对应数学关系列出边界方程
导 波 场 论 1区 2区 S=n n S=-n h E 0 H J a D a B 0 s s s s s s n ds n ds n ds n ds 对面积分,h—>0时, 忽略在小高斯盒侧面的 积分,两边消除a,有: s s J 为面电流密度 为面电荷密度 有: 1 2 1 2 1 2 1 2 E -E 0 H -H J D -D B -B 0 s s n n n n 回顾 电磁场边界条件推导 电磁边界条件的数学关系是由麦克斯韦方程推导而得 根据实际场景,按对应数学关系列出边界方程

导波场论 回顾分离变量法一纵向场解法 齐次亥姆霍兹方程 E=E,+e.E. V2E+k2E=0 H=H,+e.H. V2i+2i=0 =V,+e2 导波系统中,采用广义坐标(U,V,z)系,令: 代入到 E(,V,Z)=E(u,V)Z(Z)) 三维拉普拉斯算符号分解为: V2=V 2 0z2
导 波 场 论 齐次亥姆霍兹方程 2 2 2 2 0 0 E k E H k H t z z t z z t z E E e E H H e H e z 导波系统中,采用广义坐标(u,v,z)系,令: E E (u, v, z) (u, v) Z(z) 三维拉普拉斯算符号分解为: 2 2 2 t 2 = + z 代入到 回顾 分离变量法——纵向场解法